PDF文档回复:20241022

1 P9749 [CSP-J 2023] 公路
[题目描述]
小苞准备开着车沿着公路自驾。
公路上一共有 n 个站点,编号为从 1 到 n。其中站点 i 与站点 i+1 的距离为 vi 公里。
公路上每个站点都可以加油,编号为 i 的站点一升油的价格为 ai 元,且每个站点只出售整数升的油。
小苞想从站点 1 开车到站点 n,一开始小苞在站点 1 且车的油箱是空的。已知车的油箱足够大,可以装下任意多的油,且每升油可以让车前进 d 公里。问小苞从站点 1 开到站点 n,至少要花多少钱加油?
[输入格式]
输入的第一行包含两个正整数 n 和 d,分别表示公路上站点的数量和车每升油可以前进的距离。
输入的第二行包含 n−1 个正整数 v1,v2...vn−1,分别表示站点间的距离。
输入的第三行包含 n 个正整数 a1,a2...an,分别表示在不同站点加油的价格。
[输出格式]
输出一行,仅包含一个正整数,表示从站点 1 开到站点 n,小苞至少要花多少钱加油
[输入输出样例]
输入 #1
5 4
10 10 10 10
9 8 9 6 5输出 #1
79说明/提示
最优方案下:小苞在站点 1 买了 3 升油,在站点 2 购买了 5 升油,在站点 4 购买了 2 升油
数据规模
对于所有测试数据保证:1≤n≤10^5,1≤d≤ 10^5,1≤vi≤ 10^5,1≤ai≤ 10^5。
| 测试点 | n≤n≤ | 特殊性质 |
|---|---|---|
| 1∼5 | 8 | 无 |
| 6∼10 | 10^3 | 无 |
| 11∼13 | 10^5 | A |
| 14∼16 | 10^5 | B |
| 17∼20 | 10^5 | 无 |
- 特殊性质 A:站点 1 的油价最低。
- 特殊性质 B:对于所有 1≤i<n,vi 为 d 的倍数
2 相关知识点
1) 向上取整
数学符号
⌈ ⌉
⌈x⌉ 向上取整符号 表示大于等于 x 的最小的整数
例如
⌈13/3⌉=52) 向下取整
数学符号
⌊ ⌋
⌊x⌋ 向下取整符号 表示小于等于 x 的最大的整数
例如
⌊13/3⌋=43) 贪心算法
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择 。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的 局部最优解
例题
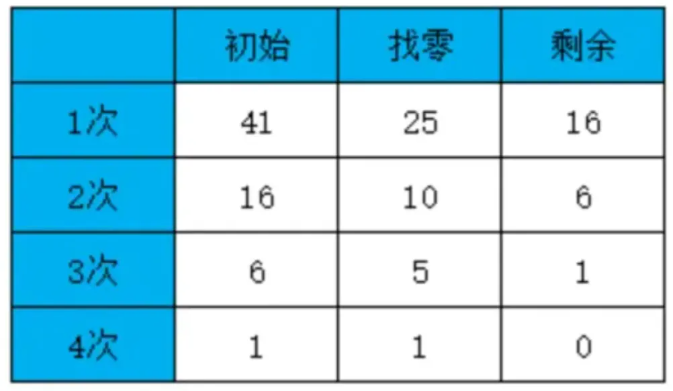
某商店不能电子支付,钱柜里的货币只有 25 分、10 分、5 分和 1 分四种硬币,如果你是售货员且要找给客户 41 分钱的硬币,如何安排才能找给客人的钱既正确且硬币的个数又最少?
分析
钱币保证最大面额大于其他小于它的面额之和,保证了每次选择最大的没有其他优于这个组合
即 选择了25 即使选择10+5+1=16都比25小
每次选择找零面额最大的,每次都是本次最优(局部最优),根据钱币面额本身的性质可知,可以保证全局最优
3 思路分析
1 从i站点走到i+1站点,需要看当前油是否够,不够(s>0)则需要加油
2 加油只需要可以开到下1个站点,此时加油时可以选择前面所有站点最小的价格(如果选择的不是当前站点价格,实际情况需要在对应站点提前加)
3 每次加油时需要保证一定可以开到下1站点,又因为站点加油必须是整数升,因此加油升数为向上取整
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;//最大站点数
int n,d;//n 站点数量 d每升油前进距离
/*
v[i] i~i+1站点的距离
a[i] i个站点加油的单价
minPrice 走i~i+1段距离时,油价,在此段找之前站点最小价格,实际情况应该在之前站点加好油
*/
int v[N],a[N],minPrice=N;//通过比较取最小,默认赋最大值
long long s,ans;//s需加油行驶的距离 ans花费的邮费
int main(){
cin>>n>>d;//输入站点数n和每升油前进的数量
for(int i=1;i<n;i++){//输入站点的距离 比站点数少1
cin>>v[i];
}
for(int i=1;i<=n;i++){//输入站点加油单价并计算走过此段需要的费用
cin>>a[i];//输入站点油价
s+=v[i];//走第i段,第i段距离累加到s
minPrice=min(minPrice,a[i]);//走第i段时,可以使用的最小油价(前面的都可以使用)
if(s>0){//行驶i段,需要加油(前面剩余的油不够行驶i段距离)
int cur=(s+d-1)/d;//需要加多少升油-对s向上取整(每个站点只能加整数升油)
ans+=minPrice*cur;//计算i段邮费累加到ans
s-=cur*d;//剩余油行驶距离,当前加整数升油,会多加一些,所以s负数表示有剩余油
}
}
cout<<ans;//输出花费的邮费
return 0;
}