【python】OpenCV—findContours（4.4）

文章目录

• 1、功能描述
• 2、代码实现
• 3、完整代码
• 4、结果展示
• 5、涉及到的库函数
• 6、参考

1、功能描述

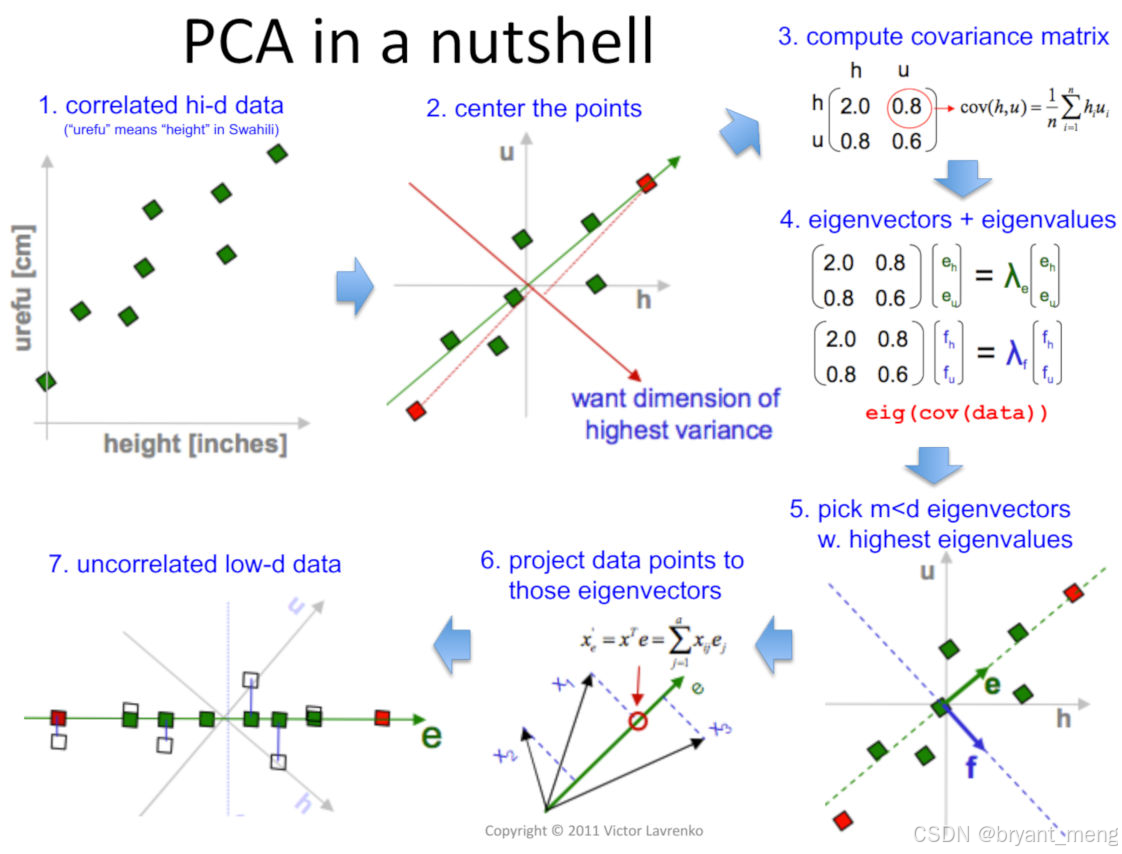
找出物体轮廓，根据 PCA 计算特征值和特征向量，绘制特征值和特征向量，来初步展示物体的方向

2、代码实现

导入库函数，读入图片，判定图片是否存在，显示图片

import cv2 as cv
from math import atan2, cos, sin, sqrt, pi
import numpy as np

# Load the image
img = cv.imread("1.jpeg")

# Was the image there?
if img is None:
    print("Error: File not found")
    exit(0)

cv.imshow('Input Image', img)

灰度化图片，二值化图片，为后续找轮廓做准备

# Convert image to grayscale
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
cv.imwrite("gray.jpg", gray)

# Convert image to binary
_, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)
cv.imwrite("bw.jpg", bw)

找轮廓

# Find all the contours in the thresholded image
contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)

遍历轮廓，剔除面积过小或者过大的轮廓，绘制轮廓，调用 getOrientation 获取物体方向并绘制，并显示绘制结果

for i, c in enumerate(contours):

    # Calculate the area of each contour
    area = cv.contourArea(c)

    # Ignore contours that are too small or too large
    if area < 1000 or 100000 < area:
        continue

    # Draw each contour only for visualisation purposes with red color
    cv.drawContours(img, contours, i, (0, 0, 255), 2)

    # Find the orientation of each shape
    getOrientation(c, img)

cv.imshow('Output Image', img)
cv.waitKey(0)
cv.destroyAllWindows()

# Save the output image to the current directory
cv.imwrite("output_img.jpg", img)

下面看看 getOrientation(c, img) 的实现

def getOrientation(pts, img):
    ## [pca]
    # Construct a buffer used by the pca analysis
    sz = len(pts)  # 轮廓的关键点数, pts (446, 1, 2)
    data_pts = np.empty((sz, 2), dtype=np.float64)  # (446, 2)
    for i in range(data_pts.shape[0]):
        data_pts[i, 0] = pts[i, 0, 0]
        data_pts[i, 1] = pts[i, 0, 1]

    # Perform PCA analysis
    mean = np.empty((0))
    mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)

    # Store the center of the object
    cntr = (int(mean[0, 0]), int(mean[0, 1]))  # (177, 349)
    ## [pca]

    ## [visualization]
    # Draw the principal components
    cv.circle(img, cntr, 3, (255, 0, 255), 2)
    p1 = (cntr[0] + 0.025 * eigenvectors[0, 0] * eigenvalues[0, 0],
          cntr[1] + 0.025 * eigenvectors[0, 1] * eigenvalues[0, 0])
    p2 = (cntr[0] - 0.025 * eigenvectors[1, 0] * eigenvalues[1, 0],
          cntr[1] - 0.025 * eigenvectors[1, 1] * eigenvalues[1, 0])

   #  乘以0.25是为了放大这个距离，使其在图像上更加明显。

    drawAxis(img, cntr, p1, (255, 255, 0), 1)
    drawAxis(img, cntr, p2, (0, 0, 255), 5)

    angle = atan2(eigenvectors[0, 1], eigenvectors[0, 0])  # orientation in radians
    ## [visualization]

    # Label with the rotation angle
    # label = "  Rotation Angle: " + str(-int(np.rad2deg(angle)) - 90) + " degrees"
    label = str(-int(np.rad2deg(angle)) - 90) + " degrees"
    textbox = cv.rectangle(img, (cntr[0]+15, cntr[1] - 50), (cntr[0] + 130, cntr[1] - 15), (255, 255, 255), -1)
    cv.putText(img, label, (cntr[0]+15, cntr[1]-25), cv.FONT_HERSHEY_SIMPLEX, 0.5, (0, 0, 0), 1, cv.LINE_AA)

    return angle

其中 cv2.PCACompute2 获取特征值和特征向量

p1、p2 是计算特征向量乘以特征值，方便后续可视化物体方向，0.025 是系数，影响的是绘制时候的长度

drawAxis 绘制箭头，展示物体方向

def drawAxis(img, p_, q_, color, scale):
    p = list(p_)
    q = list(q_)

    ## [visualization1]
    angle = atan2(p[1] - q[1], p[0] - q[0])  # angle in radians
    hypotenuse = sqrt((p[1] - q[1]) **2 + (p[0] - q[0])**2)

    # Here we lengthen the arrow by a factor of scale
    q[0] = p[0] - scale * hypotenuse * cos(angle)
    q[1] = p[1] - scale * hypotenuse * sin(angle)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), color, 3, cv.LINE_AA)

    # create the arrow hooks 绘制箭头的钩子
    p[0] = q[0] + 9 * cos(angle + pi / 4)
    p[1] = q[1] + 9 * sin(angle + pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), color, 3, cv.LINE_AA)

    p[0] = q[0] + 9 * cos(angle - pi / 4)
    p[1] = q[1] + 9 * sin(angle - pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), color, 3, cv.LINE_AA)
    ## [visualization1]

可以看到有三个 cv2.line，第一个是绘制方向的直线，第二个和第三个分别绘制箭头，偏离直线 ±45°

scale 控制箭头直线的长度

3、完整代码

import cv2 as cv
from math import atan2, cos, sin, sqrt, pi
import numpy as np


def drawAxis(img, p_, q_, color, scale):
    p = list(p_)
    q = list(q_)

    ## [visualization1]
    angle = atan2(p[1] - q[1], p[0] - q[0])  # angle in radians
    hypotenuse = sqrt((p[1] - q[1]) **2 + (p[0] - q[0])**2)

    # Here we lengthen the arrow by a factor of scale
    q[0] = p[0] - scale * hypotenuse * cos(angle)
    q[1] = p[1] - scale * hypotenuse * sin(angle)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), color, 3, cv.LINE_AA)

    # create the arrow hooks 绘制箭头的钩子
    p[0] = q[0] + 9 * cos(angle + pi / 4)
    p[1] = q[1] + 9 * sin(angle + pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), color, 3, cv.LINE_AA)

    p[0] = q[0] + 9 * cos(angle - pi / 4)
    p[1] = q[1] + 9 * sin(angle - pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), color, 3, cv.LINE_AA)
    ## [visualization1]


def getOrientation(pts, img):
    ## [pca]
    # Construct a buffer used by the pca analysis
    sz = len(pts)  # 轮廓的关键点数, pts (446, 1, 2)
    data_pts = np.empty((sz, 2), dtype=np.float64)  # (446, 2)
    for i in range(data_pts.shape[0]):
        data_pts[i, 0] = pts[i, 0, 0]
        data_pts[i, 1] = pts[i, 0, 1]

    # Perform PCA analysis
    mean = np.empty((0))
    mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)

    # Store the center of the object
    cntr = (int(mean[0, 0]), int(mean[0, 1]))  # (177, 349)
    ## [pca]

    ## [visualization]
    # Draw the principal components
    cv.circle(img, cntr, 3, (255, 0, 255), 2)
    p1 = (cntr[0] + 0.025 * eigenvectors[0, 0] * eigenvalues[0, 0],
          cntr[1] + 0.025 * eigenvectors[0, 1] * eigenvalues[0, 0])
    p2 = (cntr[0] - 0.025 * eigenvectors[1, 0] * eigenvalues[1, 0],
          cntr[1] - 0.025 * eigenvectors[1, 1] * eigenvalues[1, 0])

   #  乘以0.25是为了放大这个距离，使其在图像上更加明显。

    drawAxis(img, cntr, p1, (255, 255, 0), 1)
    drawAxis(img, cntr, p2, (0, 0, 255), 5)

    angle = atan2(eigenvectors[0, 1], eigenvectors[0, 0])  # orientation in radians
    ## [visualization]

    # Label with the rotation angle
    # label = "  Rotation Angle: " + str(-int(np.rad2deg(angle)) - 90) + " degrees"
    label = str(-int(np.rad2deg(angle)) - 90) + " degrees"
    textbox = cv.rectangle(img, (cntr[0]+15, cntr[1] - 50), (cntr[0] + 130, cntr[1] - 15), (255, 255, 255), -1)
    cv.putText(img, label, (cntr[0]+15, cntr[1]-25), cv.FONT_HERSHEY_SIMPLEX, 0.5, (0, 0, 0), 1, cv.LINE_AA)

    return angle


# Load the image
img = cv.imread("1.jpeg")

# Was the image there?
if img is None:
    print("Error: File not found")
    exit(0)

cv.imshow('Input Image', img)

# Convert image to grayscale
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
cv.imwrite("gray.jpg", gray)

# Convert image to binary
_, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)
cv.imwrite("bw.jpg", bw)

# Find all the contours in the thresholded image
contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)

for i, c in enumerate(contours):

    # Calculate the area of each contour
    area = cv.contourArea(c)

    # Ignore contours that are too small or too large
    if area < 1000 or 100000 < area:
        continue

    # Draw each contour only for visualisation purposes with red color
    cv.drawContours(img, contours, i, (0, 0, 255), 2)

    # Find the orientation of each shape
    getOrientation(c, img)

cv.imshow('Output Image', img)
cv.waitKey(0)
cv.destroyAllWindows()

# Save the output image to the current directory
cv.imwrite("output_img.jpg", img)

4、结果展示

输入图片

灰度图

二值化后的结果

绘制的方向，drawAxis(img, cntr, p2, (0, 0, 255), 1) 时

drawAxis(img, cntr, p2, (0, 0, 255), 5) 时

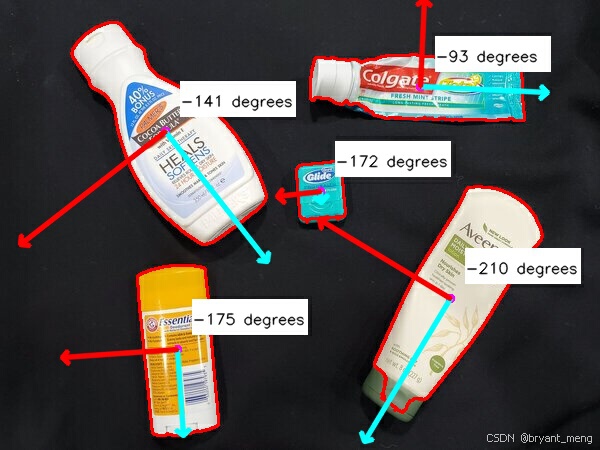
角度怎么分析呢？

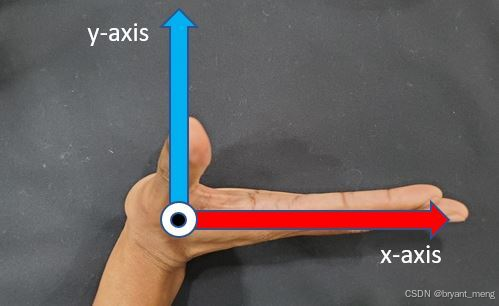
上图展示的是正方向

逆时针旋转能还原成上图情况就是负角度

仔细核对发现这个不符合上述的规则，个人理解，因为这个和正方向是反的（还原不到上述的正方向）

逆时针旋转，还原到 x 朝左，正好是 93°

5、涉及到的库函数

一、函数简介

cv2.PCACompute2 是 OpenCV 库中用于执行主成分分析（PCA）的函数。 PCA是一种统计方法，用于减少数据集的维度，同时保留数据中的主要变化特征。通过PCA，可以找到数据中的"主成分"，这些主成分定义了数据的主要变化方向。

二、函数参数

cv2.PCACompute2 函数接受多个参数，以下是其主要参数的解释：

• data_pts：一个二维NumPy数组，包含所有数据点的坐标。每个数据点由一个包含两个元素的元组（x, y）表示。
• mean：可选参数，用于指定数据点的平均值。如果未提供，OpenCV会自动计算数据点的平均值。
• eigenvectors：可选参数，用于指定特征向量。如果未提供，OpenCV会自动计算特征向量。
• eigenvalues：可选参数，用于指定特征值。如果未提供，OpenCV会自动计算特征值。
• noise_cov：可选参数，用于指定噪声的协方差矩阵。如果未提供，OpenCV会使用单位协方差矩阵。
• flags：可选参数，用于指定计算方式。默认值为0，表示使用OpenCV内置的计算方式。
• iterations：可选参数，用于指定迭代次数。默认值为0，表示使用OpenCV内置的迭代次数。
• eigenvalue_threshold：可选参数，用于指定特征值阈值。如果特征值小于这个阈值，它们将被忽略。默认值为0.0，表示不使用阈值。
• eigenvector_threshold：可选参数，用于指定特征向量阈值。如果特征向量的模小于这个阈值，它们将被忽略。默认值为0.0，表示不使用阈值。

三、函数返回值

cv2.PCACompute2 函数返回以下三个值：

• mean：数据点的平均值。
• eigenvectors：特征向量。这些特征向量指向PCA认为信息最丰富的方向。
• eigenvalues：特征值。特征值表示了对应特征向量方向上的方差大小。

四、使用示例

以下是一个使用 cv2.PCACompute2 函数的简单示例：

import numpy as np  
import cv2  
  
# 生成一组多元正态分布的数据  
mean = [20, 20]  
cov = [[5, 5], [5, 25]]  
X = np.random.multivariate_normal(mean, cov, 500)  
  
# 执行PCA计算  
mean, eigenvectors, eigenvalues = cv2.PCACompute2(X.T)  
  
# 输出结果  
print("Mean:", mean)  
print("Eigenvectors:\n", eigenvectors)  
print("Eigenvalues:\n", eigenvalues)

在这个示例中，我们首先生成了一组多元正态分布的数据，然后使用 cv2.PCACompute2 函数执行PCA计算，并输出平均值、特征向量和特征值。

五、注意事项

在使用 cv2.PCACompute2 函数之前，需要确保已经安装了OpenCV库。

• 输入的 data_pts 参数应该是一个二维 NumPy 数组，且每个数据点应该由一个包含两个元素的元组（x, y）表示。
• 根据实际需求，可以选择性地提供 mean、eigenvectors、eigenvalues、noise_cov 等参数。如果未提供这些参数，OpenCV会自动计算它们。
• 返回值中的 eigenvectors 和 eigenvalues 分别表示了数据的主成分方向和对应的特征值大小。这些结果可以用于进一步的数据分析和处理。

通过合理使用该函数，可以有效地减少数据的维度并提取出数据中的主要变化特征。

6、参考

• 使用OpenCV如何确定一个对象的方向
• https://automaticaddison.com/how-to-determine-the-orientation-of-an-object-using-opencv/