前言
许多算法的本质是统计。线段树用于统计,是沟通原数组与前缀和的桥梁。
《统计的力量》清华大学-张昆玮
关于线段树
前置知识:线段树 OIWiki。
线段树是一种专门维护区间问题 的数据结构。
线段树对信息进行二进制化处理 并在树形结构上维护,以此让处理速度达到 \(O(\log{n})\) 级别。
线段树的实现方式
由于线段树的树形结构特点,每次修改查询可以从根节点向下二分查找需要用到的节点,因此较为普遍且快捷的线段树会使用递归实现。
但递归实现的线段树由于每次要从根节点递归 向下传递子树信息,导致常数较大,容易被卡常,所以出现了常数更小的递推实现的线段树(膜拜 zkw 大佬)。
zkw 线段树
先来讲一些小原理。
一、原理
由于递归 实现的线段树不是一棵满二叉树,其叶子节点位置不确定,导致每次操作都需要从根节点开始自上而下递归依次寻找叶子节点,回溯时进行维护,递归过程常数就比较大了。
所以 zkw 线段树就直接建出一棵满二叉树 ,原序列信息都维护在最底层。严格规定 父子节点关系,同层节点的子树大小相等。
这样每个叶子节点都可以直接找到并修改,由于二叉树父子节点的二进制关系 ,就可以递推直接找到对应节点的父亲节点自下而上地维护节点关系。
二、初始化
1、建树
对长度为 \(n\) 的序列建一棵 zkw 线段树,其至少有 \(n+2\) 个叶子节点 。其中有 2 个用来帮助维护区间信息的虚点 ,有 \(n\) 个用来存原序列信息的节点。
如图(【模板】线段树 1的样例为例,下同):
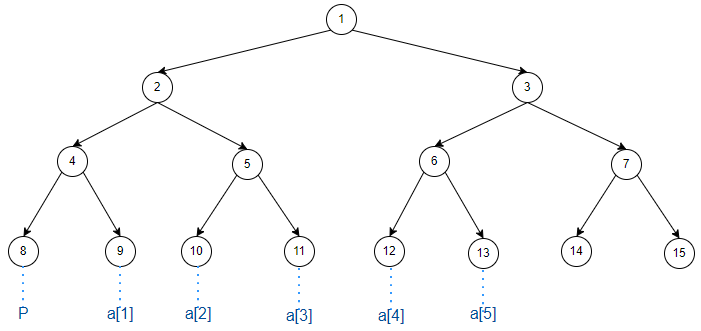
建树时先求出虚点 \(P\) 位置,然后直接向其他叶子节点读入信息即可:
cpp
//先求虚点 P
P = 1;
while(P<=n+1) P<<=1;//节点深度每增加一层,当前层节点数量扩大一倍
for(int i=1;i<=n;++i) read(tr[P+i]);2、维护
根据上文所说,由于严格确定了父子关系,所以直接自下而上遍历所有节点维护父子关系做初始化:
cpp
//push_up
for(int i=P-1;i;--i){//i=(P+n)>>1
tr[i] = tr[i<<1|1]+tr[i<<1];
tr[i] = min(tr[i<<1|1],tr[i<<1]);
tr[i] = max(tr[i<<1|1],tr[i<<1]);
//...
}三、概念介绍
1、永久化懒标记
与递归线段树的 \(lazy\) \(tag\) 不同,其每次向下递归时都需要先下放标记并清空以维护信息。
但在维护存在结合律 的运算时,zkw 线段树的 \(lazy\) \(tag\) 只会累加,而不会在修改和查询前下放清空。
2、"哨兵"节点
在区间操作时,引入两个哨兵节点,分别在区间的左右两侧,把闭区间变成开区间进行处理。
两个哨兵节点到根有两条链,与两条链相邻且在中间部分的节点,就是这次操作需要用到其信息的所有节点。
如图(沿用了第一个图,节点中的数的为区间和):
例如:【模板】线段树 1第一个操作 \(query(2,4)\):
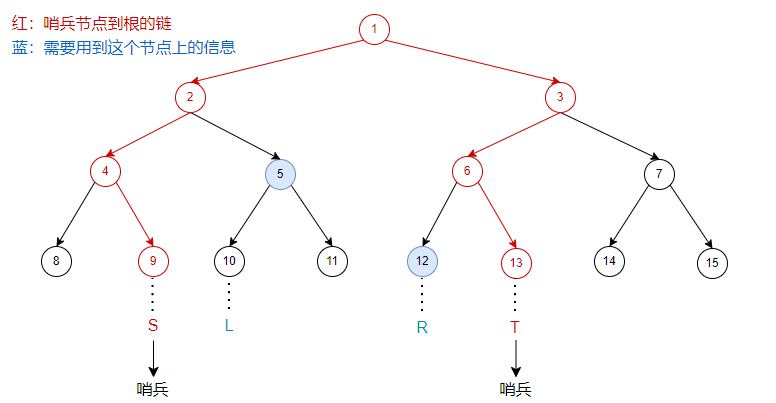
同时,这也解释了为什么建树时叶子节点上会有 \(2\) 个虚点(当然是为了不越界)。
(1)为什么可以确定需要用到哪些节点
操作时,只需要操作区间中单元素区间的公共祖先即可。
我们选取的两条链,中间部分正好包含了与操作区间有关的所有节点,与两条链相邻的节点显然的所有区间的公共祖先。
操作时只需要操作这些节点上的信息就可以了。
(2)在递推过程中怎么判断要用到哪些节点
观察我们刚才手推出来的图片,注意到:
对于左哨兵 \(S\),当它是左儿子时,其兄弟节点是需要用到的;
对于右哨兵 \(T\),当它是右儿子时,其兄弟节点是需要用到的。
每次操作完后 \(S\) 和 \(T\) 向上走到自己的父亲节点,然后维护父子关系,再进行新一轮操作。
当 \(S\) 和 \(T\) 互为兄弟节点时(走到了两条链的交点),就停止操作,然后向上维护信息到根节点。
四、基于结合律的查询与修改
1、区间修改
以区间加为例 。
类似递归线段树操作,更新时需要知道当前节点的子树大小 。
每次更新时,当前节点的值增加的是其标记乘子树大小;其标记的值正常累加即可。
永久化懒标记减少了标记下放带来的常数。
cpp
//
inline void update_add(int l,int r,ll k){
l=P+l-1; r=P+r+1;//哨兵位置
int siz = 1;//记录当前子树大小
while(l^1^r){//当l与r互为兄弟时,只有最后一位不同
if(~l&1) tr[l^1]+=siz*k,sum[l^1]+=k;
if(r&1) tr[r^1]+=siz*k,sum[r^1]+=k;
//类似递归线段树 tr[p] += tag[p]*(r-l+1)
l>>=1; r>>=1; siz<<=1;
//每次向上走时子树大小都会增加一倍
tr[l] = tr[l<<1]+tr[l<<1|1]+sum[l]*siz;//维护父子关系
tr[r] = tr[r<<1]+tr[r<<1|1]+sum[r]*siz;
}
for(l>>=1,siz<<=1;l;l>>=1,siz<<=1) tr[l] = tr[l<<1]+tr[l<<1|1]+sum[l]*siz;//更新上传至根节点
} 2、区间查询
由于我们需要查询的区间被左右哨兵分为了两个部分,但两部分子树大小不一定相等。
所以要分别维护左右哨兵到达的节点所包含查询区间的子树的大小。
cpp
//
inline ll query_sum(int l,int r){
l=l+P-1; r=r+P+1;
ll res = 0;
int sizl = 0,sizr = 0,siz = 1;//分别维护左右两侧子树大小
while(l^1^r){
if(~l&1) res+=tr[l^1],sizl+=siz;//更新答案及子树大小
if(r&1) res+=tr[r^1],sizr+=siz;
l>>=1; r>>=1; siz<<=1;
res += sum[l]*sizl+sum[r]*sizr;
//即使当前节点所存的区间和不需要用,但因为其是两个哨兵的父亲节点,且 tag 不会下传,
//所以其 tag 会对答案有贡献,所以需要加上 tag 的贡献
}
for(l>>=1,sizl+=sizr;l;l>>=1) res+=sum[l]*sizl;//累加至根节点
return res;
}如果维护区间最大值也同理:
cpp
//
inline void update_add(int l,int r,ll k){
l=P+l-1; r=P+r+1;
while(l^1^r){
if(~l&1) sum[l^1]+=k,maxn[l^1]+=d;
if(r&1) sum[r^1]+=k,maxn[r^1]+=d;
l>>=1; r>>=1;
maxn[l] = max(maxn[l<<1],maxn[l<<1|1])+sum[l];
maxn[r] = max(maxn[r<<1],maxn[r<<1|1])+sum[r];
}
for(l>>=1;l;l>>=1) maxn[l]=max(maxn[l<<1],maxn[l<<1|1])+sum[l];//更新上传至根节点
}
inline ll query_max(int l,int r){
l=l+P-1; r=r+P+1;
ll resl = 0,resr = 0;//分别记录左右两侧最大值
while(l^1^r){
if(~l&1) resl=max(resl,maxn[l^1]);
if(r&1) resr=max(resr,maxn[r^1]);
l>>=1; r>>=1;
resl += sum[l];//标记永久化,所以要累加标记值
resr += sum[r];
}
for(resl=max(resl,resr),l>>=1;l;l>>=1) res1+=sum[l];//累加至根节点
return resl;
}某些时候,只会用到单点修改区间查询和区间修改单点查询,此时 zkw 线段树码量优势很大。
3、单点修改下的区间查询
修改:直接改叶子结点的值然后向上维护。
查询:哨兵向上走时直接累加节点值。
cpp
//
inline update(int x,ll k){
x += P; tr[x] = k;
for(x>>=1; x ;x>>=1) tr[x] = tr[x<<1]+tr[x<<1|1];
}
inline ll query(int l,int r){
l += P-1; r += P+1;
ll res = 0;
while(l^1^r){
if(~l&1) res+=tr[l^1];
if(r&1) res+=tr[r^1];
l>>=1; r>>=1;
}
return res;
}4、区间修改下的单点查询
将赋初值的过程看作是在叶子节点上打标记,区间修改也是在节点上打标记。
由于 zkw 线段树的标记是永久化的,所以此时将标记的值看作节点的真实值。
但这种做法显然只对于单点查询有效,在查询时需要加上节点到根沿途的所有标记。
cpp
//
inline void update_add(int l,int r,ll k){
l += P-1; r += P+1;
while(l^1^r){
if(~l&1) tr[l^1]+=k;
if(r&1) tr[r^1]+=k;
l>>=1; r>>=1;
}
}
inline ll query(int x){
ll res = 0;
for(x+=P; x ;x>>=1) res+=tr[x];
return res;
}5、标记永久化的局限性
以上修改与查询方式,全部基于运算具有结合律,所以标记可以永久化,以此减少标记下放增加的常数。
但如果运算存在优先级,标记就不能再永久化了。考虑在更新时将先标记下放(类似递归线段树)然后再从叶子节点向上更新。
但是如果像递归线段树一样从根开始逐次寻找子节点下放一遍的话,那优化等于没有。
所以要考虑基于 zkw 线段树的特点进行下放操作,而且要尽可能的简洁方便。
So easy,搜一紫衣。
五、有运算优先级的修改与查询
1、标记去永久化
在进行区间修改时,我们会用到的节点只存在于哨兵节点到根的链上。
所以只考虑将这两条链上的节点标记进行下放即可。
(1)如何得到有哪些需要下放标记的节点
考虑最暴力的方法:
每次从哨兵节点向上递归直至根节点,回溯时下放标记。
显然这样的方式常数优化约等于零。
考虑优化肯定是基于 zkw 线段树的特点。
还是由于 zkw 线段树是满二叉树结构,所以可以通过节点编号移位 的方式找到其所有父子节点的编号。
显然哨兵到根节点的链,是哨兵的所有父亲组成的,所以只要让哨兵编号移位就可以了。
(2)如何自上而下的传递标记
再记录一下叶子节点的深度。
思考满二叉树的性质:当节点编号右移位节点深度时就指向根节点编号。
所以节点右移的位数,从节点深度依次递减,就可以自上而下得到其所有父亲节点的编号。
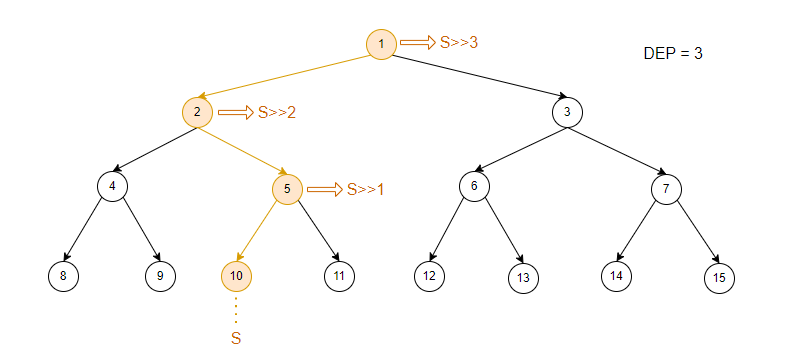
2、区间修改
先下放标记,然后正常做标记更新。
传递标记时可能要考虑子树大小,直接通过深度计算就可以了。
以区间加及乘为例:
cpp
//建树时记录叶子节点深度
P = 1;DEP = 0;
while(P<=n+1) P<<=1,++DEP;
//...
//...
//...
inline void update_add(int l,int r,ll k){
l=P+l-1; r=P+r+1;
//先下放标记
for(int i=DEP;i;--i) push_down(l>>i,1<<i),push_down(r>>i,1<<i);
//push_dwon( 链上节点 , 当前子树大小 );
int siz = 1;
while(l^1^r){
if(~l&1) tr[l^1]+=siz*k,sum[l^1]+=k;//正常更新
if(r&1) tr[r^1]+=siz*k,sum[r^1]+=k;
l>>=1; r>>=1; siz<<=1;
//维护父子关系
tr[l] = tr[l<<1]+tr[l<<1|1];//由于标记已下放,所以维护时不再考虑累加标记
tr[r] = tr[r<<1]+tr[r<<1|1];
}
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];//上传至根节点
}
//
inline void update_mul(int l,int r,ll k){
l += P-1; r += P+1;
for(int i=DEP;i;--i) push_down(l>>i,1<<i),push_down(r>>i,1<<i);
while(l^1^r){
if(~l&1) tr[l^1]*=k,mul[l^1]*=k,sum[l^1]*=k;//标记覆盖
if(r&1) tr[r^1]*=k,mul[r^1]*=k,sum[r^1]*=k;
l>>=1; r>>=1;
tr[l] = tr[l<<1]+tr[l<<1|1];
tr[r] = tr[r<<1]+tr[r<<1|1];
}
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];
}3、区间查询
先下放标记。
由于标记已经去永久化,所以直接累加节点值即可。
cpp
//
inline ll query(int l,int r){
l = l+P-1;r = r+P+1;
//先下放标记
for(int i=DEP;i;--i) push_down(l>>i,1<<i),push_down(r>>i,1<<i);
ll res = 0;
while(l^1^r){
if(~l&1) res+=tr[l^1];
if(r&1) res+=tr[r^1];
//由于标记已下放,所以无需再累加标记的贡献
l>>=1; r>>=1;
}
return res;
}六、优化效果
1、时间复杂度
开始的时候也提到了:递归线段树常数大的瓶颈在于其需要对树进行递归遍历 以找到目标节点,然后回溯进行信息维护。
zkw 线段树仅仅只是 优化了递归寻找目标节点这样的遍历过程的常数。
如果是追求常数或者注重优化遍历,那 zkw 线段树的优化就比较明显了;如果要维护较为复杂的信息,那么显然这点常数并不是很够看,此时就需要在其他地方上做改进了。
2、空间复杂度
zkw 线段树需要开三倍空间,普通线段树如果不使用动态开点需要开四倍空间。
相较于普通线段树,zkw 线段树代码好理解也比较简洁,不会出现忘建树 和忘终止递归 的问题,而且满二叉树结构的确定性让手造数据 也比较方便。
对于一些维护信息复杂的题目,zkw 线段树的优势在于手推时思路更加清晰。
如果性格比较内向,不敢用递归线段树进行递归维护信息。
想用 zkw 递推实现更多更强的操作怎么办!
zkw 线段树实现其他线段树结构
一、引入
1、关于 zkw 线段树
本人认为:狭义 的 zkw 线段树是指建立出满二叉树结构、节点间的父子关系严格规定、一切信息从叶子节点开始向上维护、通过循环递推实现维护过程。
另外:张昆玮大佬的 PPT 中提到,为了减小递归带来的常数,出现了汇编版的非递归 线段树。
所以本人的理解是:广义 的 zkw 线段树指通过循环递推而非递归实现的线段树。
2、关于优化效果
基于多数线段树结构的特点,导致大部分时候必须上下循环两次维护信息,所以此时 zkw 线段树更多优化的是代码的简洁程度 和理解难度(当然了,对常数也有一些优化)。
二、可持久化线段树
1、介绍
可持久化线段树与普通线段树的区别在于,其支持修改和访问任意版本 。
举个例子:给定一个序列 \(a_N\),对它进行一百万次操作,然后突然问你第十次操作后的序列信息。
朴素的想法是对于每次操作都建一棵线段树,空间复杂度是 \(O(3mn)\) 的。
可以发现:
修改后,大部分节点并没有受到影响,所以考虑只对受影响的节点新建对应节点。其余没受影响的节点直接与原树共用节点,就等同于新建了一棵修改后的线段树。
2、单点修改单点查询
每次单点修改后,只有叶子节点到根节点的那一条链上的点会受到影响。
所以我们只需要对受影响的这条链新建一条对应的链,其余没受影响的节点直接和待修改版本共用即可。
对于本次要修改的位置,在以原始序列 \(a_N\) 建立的初始线段树中,其对应的叶子节点到根的链上的节点分别为 \(tl\),当前新节点为 \(now\),下一个新节点为 \(new\):
如果 \(tl\) 为左儿子,那么 \(now\) 的左儿子为 \(new\),右儿子为 \(tl\) 对应在待修改树上节点的兄弟节点;
如果 \(tl\) 为右儿子,那么 \(now\) 的右儿子为 \(new\),左儿子为 \(tl\) 对应在待修改树上节点的兄弟节点。
其实就是新建节点的位置与初始树上的节点位置分别对应 。
看图(节点内数字为节点编号):在原序列上修改一个位置:
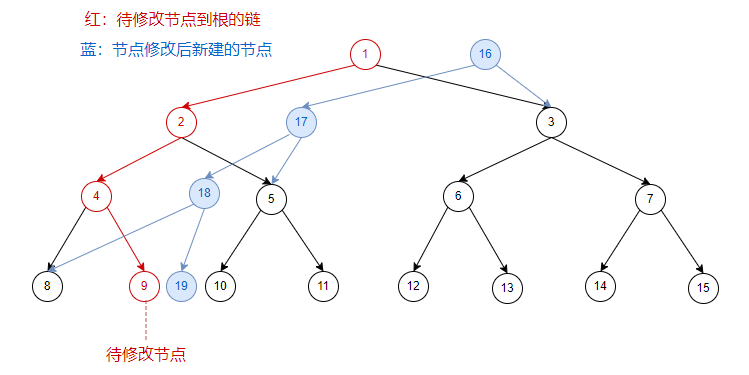
在第一次修改后的序列上,再修改一次:
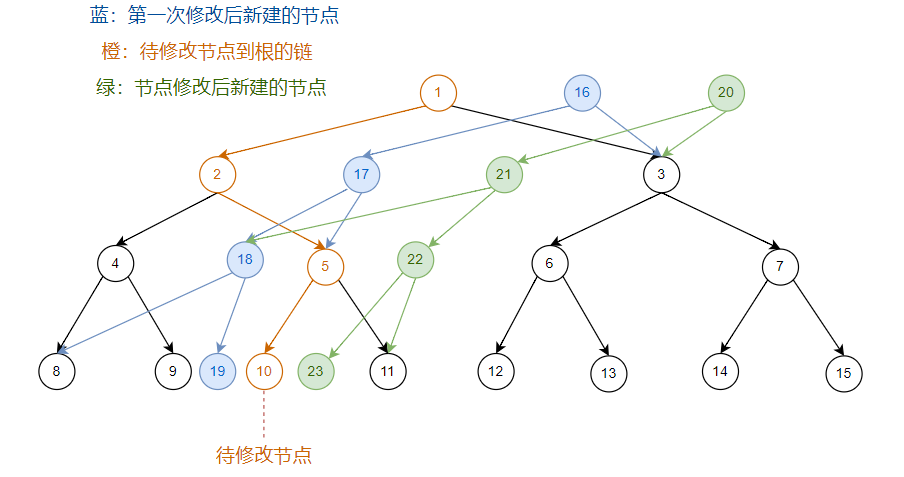
继续在第一次修改后的序列上做修改:
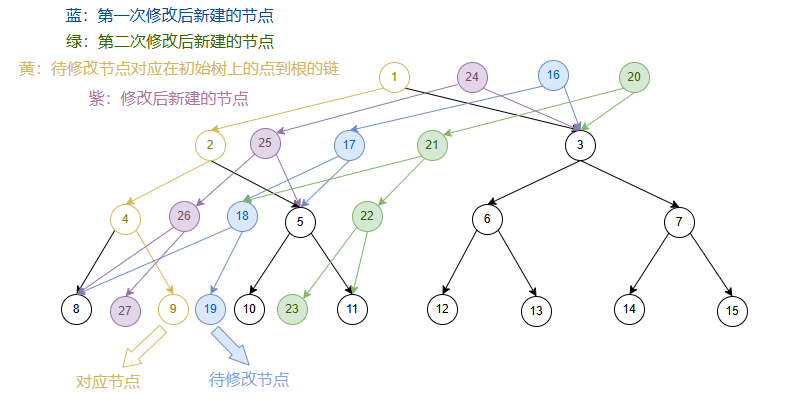
我们发现新建的链在新树上的位置,与初始树上的链在初始树上的位置,是相同 的。
所以我们新建节点时,新节点的位置跟随 对应的初始树上的节点的位置进行移动。
由于版本间需要以根节点做区分 (因为使用叶子节点会非常麻烦),所以修改和查询 操作只能从根节点开始自上而下 进行,防止不同版本的存储出现问题。
所以我们需要多一个记录:当前节点的左右儿子。
对于 \(tl\) 到根的链如何快速求得,我们前面讲"哨兵"的时候已经讲过实现,接下来就是模拟整个新建节点过程即可。
同时,新建节点的节点编号依次递增,操作后进行自下而上维护信息也很方便:
cpp
//建初始线段树
while(P<=n+1) P<<=1,++DEP; NOW = (1<<(DEP+1))-1;//最后一个节点的编号
for(int i=1;i<=n;++i) read(tr[P+i]); rt[0] = 1;//初始树根为1
for(int i=P-1;i;--i) son[i][0]=i<<1,son[i][1]=i<<1|1;//记录子节点 0为左儿子;1为右儿子
//...
//...
inline void update(int i,int vi,int val,int l){
int tl = l+P;//在初始树上对应的叶子节点编号
int v = rt[vi];//待修改线段树的根
rt[i] = l = ++NOW;//新线段树的根
for(int dep=DEP-1; dep>=0 ;--dep,l = NOW){
//模拟节点更新过程
if((tl>>dep)&1) son[l][0] = son[v][0],son[l][1] = ++NOW,v = son[v][1];
else son[l][0] = ++NOW,son[l][1] = son[v][1],v = son[v][0];
}
tr[l] = val;//更新最后的叶子节点
//自下而上维护信息(如果有需要的话)
//for(int dep=1;dep<=DEP;++dep) tr[l-dep]=tr[son[l-dep][0]]+tr[son[l-dep][1]];
}版本查询与修改相同,从根开始模拟子树选取:
cpp
//
inline int query(int vi,int l){
int tl = l+P;//在初始树上对应的叶子节点编号
l = rt[vi];//当前版本的根
for(int dep=DEP-1; dep>=0 ;--dep) l=son[l][(tl>>dep)&1];
return tr[l];//返回叶子节点值
}3、区间修改区间查询
目前我了解到的信息是:只能做区间加 。
可持久化线段树中有大量的公用节点,所以标记不能下放且修改要能够用永久化标记维护,否则会对其他版本产生影响。
那么考虑如何做区间加。
- 标记永久化:省去标记下放以减小常数同时防止对其他版本产生影响;
- 预处理时记录子树大小,查讯时累加标记值。
不同的是:
- 需要对区间新建节点;
- 修改时对照初始树上节点的轨迹进行移动;
- 修改需要自上而下进行,然后再自下而上做一遍维护(类似递归回溯)。
三、权值线段树
1、介绍
普通线段树维护的是信息,权值线段树维护的是信息的个数 。
权值线段树相当于在普通线段树上开了一个桶 ,用于处理信息个数,以单点修改和区间查询 实现动态全局第 \(k\) 大。
2、查询全局排名
在权值线段树中,节点存信息出现的次数:
cpp
//
inline void update(int l,int k){
l += P; tr[l] += k;//k为信息出现次数
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];
}当前数字的相对大小位置向前的前缀和,即为当前数字在全局中的排名:
cpp
//
inline int get_rank(int r){//查询第r个数的全局排名
int l = 1+P-1;//做区间[1,r]的前缀和
r += P+1;
int res = 0;
while(l^1^r){
if(~l&1) res+=tr[l^1];
if(r&1) res+=tr[r^1];
l>>=1; r>>=1;
}
return res;
}3、动态全局第 \(k\) 大
基于线段树的结构,第 \(k\) 大的二分 实现其实就在线段树上查找左右子树 的过程。
查询第 \(k\) 大时,借助线段树的结构,以左右子树选取来模拟二分过程即可:
cpp
//
inline int K_th(int k){
int l = 1,dep = 0;
while(dep<DEP){
if(tr[l<<1]>=k) l=l<<1;//模拟二分
else k-=tr[l<<1],l=l<<1|1;
++dep;
}
return l-P;//减去虚点编号,得到原数组中的编号
}4、前驱与后继
有时还需要查询 \(k\) 的前驱和后继。
\(k\) 的前驱为:最大的小于 \(k\) 的数;
\(k\) 的后继为:最小的大于 \(k\) 的数。
查 \(k\) 的前驱可以看作:查与 \(k-1\) 的排名相同数;
查 \(k\) 的后继可以看作:查比 \(k\) 的排名靠后一位的数。
结合一下 \(get\_rank\) 和 \(K\_th\) 即可:
cpp
//
inline int pre(int k){
int rk = get_rank(k-1);
return K_th(rk);
}
inline int nex(int k){
int rk = get_rank(k)+1;
return K-th(rk);
}四、可持久化权值线段树(主席树)
有人说 zkw 做不了主席树,我急了。
1、介绍
顾名思义,就是可持久化线段树和权值线段树 结合。
大部分情况下只需要支持区间查询,常用于解决静态区间第 \(k\) 大 ,因为单独的主席树不太好进行修改操作。
当然,动态区间第 \(k\) 大 的实现------树套树,可以直接跳到目录五去看。
2、静态区间第 \(k\) 大
主席树对序列的每个位置都维护一棵线段树,其节点值为对应序列上值的范围。
在第 \(m\) 棵线段树上,区间 \([L,R]\) 维护的是:序列上 \(a_i\sim a_m\) 中,有多少数字在 \([L,R]\) 范围内。
我们对序列中每一个数的权值 都开一棵线段树,一共开 \(N\) 棵树,存不下,所以使用可持久化线段树。
由于权值线段树存下了数的权值,每个节点上存的是前缀和,信息具有可加性。所以查 \([L,R]\) 等于查 \([1,R]-[1,L-1]\)。
可持久化线段树的新建书和权值线段树的查询结合一下就好了:
cpp
//可持久化线段树的建新树
inline void update(int i,int vi,int l,int k){
int tl = l+P;
int v = rt[vi];
rt[i] = l = ++NOW;
for(int dep=DEP-1; dep>=0 ;--dep,l=NOW){
if((tl>>dep)&1) son[l][0] = son[v][0],son[l][1] = ++NOW,v = son[v][1];
else son[l][1] = son[v][1],son[l][0] = ++NOW,v = son[v][0];
}
tr[l] = tr[v]+k;//需要维护前缀和
//向上维护信息
for(int dep=1;dep<=DEP;++dep) tr[l-dep]=tr[son[l-dep][0]]+tr[son[l-dep][1]];
}
//权值线段树的查询
inline int query(int l,int r,int k){
//查 [l,r] 相当于查 [1,r]-[1,l-1]
l = rt[l-1];r = rt[r];
int tl = 1;//答案
for(int dep=0;dep<DEP;++dep){
int num = tr[son[r][0]]-tr[son[l][0]];//左子树大小
if(num>=k){//不比左子树大,说明在左子树中
l = son[l][0];
r = son[r][0];
tl = tl<<1;
}
else{//比左子树大,说明在右子树中
k -= num;
l = son[l][1];
r = son[r][1];
tl = tl<<1|1;
}
}
return tl-P;//当前权值为:对应在初始树上位置减虚点编号
}五、树状数组套权值线段树
1、介绍
上文说,单独的主席树不方便维护动态区间第 \(k\) 大 ,主要是因为主席树修改时,对应的其他版本关系被破坏了。
实现动态第 \(k\) 大的朴素想法当然还是对序列的每个位置都开一棵权值线段树,那么难点就在于我们到底要对哪些树做修改。
由于权值线段树具有可加性 的性质,所以我们可以拿一个树状数组维护线段树的前缀和,用于求出要修改哪些树。这个过程我们可以用 \(lowbit\) 来实现。
把要修改的树编号存下来,然后做线段树相加的操作,此时操作就从多棵线段树变成了在一棵线段树上操作。
2、初始化
对序列的每个点建一棵 zkw 线段树的话,空间会变成 \(Q(3n^2)\) 的,所以我们需要动态开点 ,空间复杂度变成 \(O(n\log^2{n})\)。
(存个节点而已,我们 zkw 也要动态开点,父子关系对应初始树就可以了)。
为了保证修改和查询时新树节点与序列的对应关系,以及严格确定的树形结构,所以我们先建一棵初始树(不用真的建出来,因为我们只会用到编号 ),操作时新树上的节点跟随对应在初始树上的节点进行移动。
cpp
//
for(int i=1;i<=n;++i){
read(a[i]);
b[++idx] = a[i];
}
sort(b+1,b+1+idx);
idx = unique(b+1,b+1+idx)-(b+1);//离散化
while(P<=idx+1) P<<=1,++DEP;//求初始树上节点编号备用
for(int i=1;i<=n;++i){
a[i] = lower_bound(b+1,b+1+idx,a[i])-b;
add(i,1);//对每个位置建线段树
}
//...
inline void update(int i,int l,int k){
int tl = l+P,stop = 0;
rt[i] ? 0 : rt[i]=++NOW;//动态开点
l = rt[i]; st[++stop] = l;tr[l] += k;
for(int dep=DEP-1;dep>=0;--dep,st[++stop]=l,tr[l]+=k){
if((tl>>dep)&1) son[l][1]?0:son[l][1]=++NOW,l=son[l][1];
else son[l][0]?0:son[l][0]=++NOW,l=son[l][0];
}
//为了方便也可以把链上的节点全存下来再做维护
//while(--stop) tr[st[stop]] = tr[son[st[stop]][0]]+tr[son[st[stop]][1]];
}
inline void add(int x,int k){//lowbit求需要用到的线段树
for(int i=x;i<=n;i+=(i&-i)) update(i,a[x],k);
}3、单点修改
先把原来数的权值减一,再让新的数权值加一。
cpp
//
inline void change(int pos,int k){
add(pos,-1);
a[pos] = k;
add(pos,1);
}4、查询区间排名
由于权值线段树维护的是前缀和,所以把区间 \([L,R]\) 的查询看作查询 \([1,R]-[1,L-1]\)。
先用树状数组求出需要用到的线段树,然后做线段树相加,求前缀和即可。
cpp
//
inline int query_rank(int l){
l += P;
int res = 0;
for(int dep=DEP-1;dep>=0;--dep){
if((l>>dep)&1){//做线段树相加求前缀和
for(int i=1;i<=tmp0;++i) res-=tr[son[tmp[i][0]][0]],tmp[i][0]=son[tmp[i][0]][1];
for(int i=1;i<=tmp1;++i) res+=tr[son[tmp[i][1]][0]],tmp[i][1]=son[tmp[i][1]][1];
}
else{
for(int i=1;i<=tmp0;++i) tmp[i][0]=son[tmp[i][0]][0];
for(int i=1;i<=tmp1;++i) tmp[i][1]=son[tmp[i][1]][0];
}
}
return res;
}
inline int get_rank(int l,int r,int k){
tmp0 = tmp1 = 0;
for(int i=l-1; i ;i-=(i&-i)) tmp[++tmp0][0] = rt[i];
for(int i=r; i ;i-=(i&-i)) tmp[++tmp1][1] = rt[i];
return query_rank(k)+1;
//query_rank求的是小于等于k的数的个数,加一就是k的排名
}5、动态区间第 \(k\) 大
和查询排名道理一样:由于权值线段树维护的是前缀和,所以把区间 \([L,R]\) 的查询看作查询 \([1,R]-[1,L-1]\)。
还是先用树状数组求出需要用到的线段树,查询时做线段树相加。然后模拟线段树上二分就可以了。
cpp
//
inline int query_num(int k){
int l = 1;
for(int dep=0,res=0;dep<DEP;++dep,res=0){
for(int i=1;i<=tmp0;++i) res-=tr[son[tmp[i][0]][0]];
for(int i=1;i<=tmp1;++i) res+=tr[son[tmp[i][1]][0]];//每棵树的节点值都满足可加
if(k>res){
k -= res;//做树上二分
for(int i=1;i<=tmp0;++i) tmp[i][0]=son[tmp[i][0]][1];
for(int i=1;i<=tmp1;++i) tmp[i][1]=son[tmp[i][1]][1];
l = l<<1|1;
}
else{
for(int i=1;i<=tmp0;++i) tmp[i][0]=son[tmp[i][0]][0];
for(int i=1;i<=tmp1;++i) tmp[i][1]=son[tmp[i][1]][0];
l = l<<1;
}
}
return l-P;//叶子节点对应编号
}
inline int get_num(int l,int r,int k){
tmp0 = tmp1 = 0;//先用lowbit求需要查询的线段树
for(int i=l-1; i ;i-=(i&-i)) tmp[++tmp0][0] = rt[i];
for(int i=r; i ;i-=(i&-i)) tmp[++tmp1][1] = rt[i];
return query_num(k);
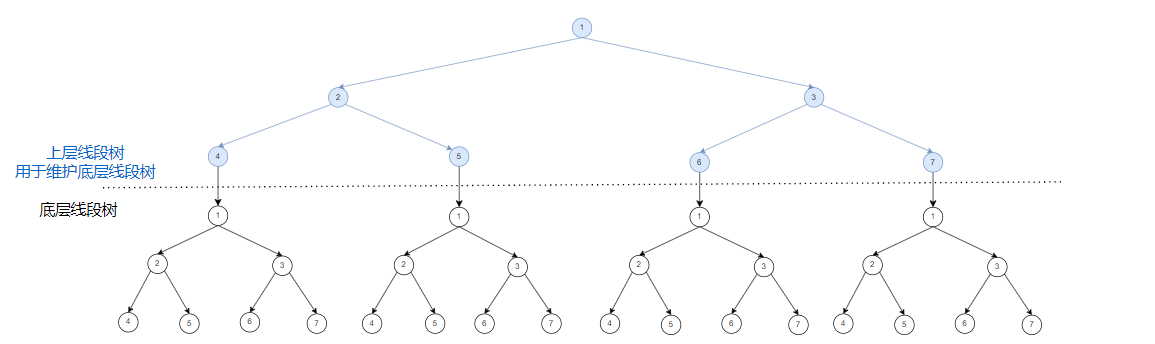
}线段树套线段树 与其原理相同。下层线段树维护序列信息,再用一棵上层线段树来维护下层线段树的前缀和。
你可以看这张图,我暂时先不多赘述了:(真的码不动字了)
六、兔队线段树
(本人不是特别了解,所以暂时仅作信息具有可加减性 的解释)
有人说 zkw 做不了兔队线段树,我急了。
1、介绍
兔队线段树是指一类:在信息修改同时 ,以 \(O(\log{n})\) 复杂度做维护的线段树。支持单点修改区间查询,通常用来维护前缀最大值 的问题。
(粉兔在这篇文章中率先对其进行了说明)
2、处理与维护
其处理与维护信息的大致方式可以看作:
- 首先修改信息,然后从下到上做维护;
- 向上维护时每到达一个节点,都再次从下到上维护信息;
- 第二次从下到上维护时,左子树对答案贡献不变,只考虑右子树对答案的贡献。
由于第一次向上维护时,需要从当前节点开始对其所有子树进行第二次维护,所以递归线段树常用的方法是二次递归处理右子树信息。
3、具体实现
考虑如何用 zkw 线段树递推 处理右子树信息。
首先,对单点进行修改后,从下到上进行处理和维护,同时记录节点深度,防止第二次维护时发生越界:
cpp
//单点修改后,每次上传更新到根节点
inline void update(int l,ll k){
l += P;int dep = DEP;
mx[l] = k;mn[l] = k;//...
for(l>>=1,--dep; l ;l>>=1,--dep) push_up(l,dep);
}然后,再次模拟标记上传过程:
cpp
//
inline void push_up(int l,int dep){
mx[l] = max(mx[l<<1],mx[l<<1|1]);
//...
ans[l] = ans[l<<1]+calc(l<<1|1,dep+1,mx[l<<1]);
}
inline int calc(int l,int dep,ll mx){
int res = 0,tl = l;
while(dep<DEP){//模拟左右子树选取过程
if(mx[l]<=k) break;//剪枝之类的
if(mx[l<<1]<=k) l = l<<1|1;
else{
res += len[l]-len[l<<1];//信息有可减性,考虑左区间的覆盖
l <<= 1;
}
++dep;
}
if(dep==DEP) res += (mx[l]>k);//叶子节点特判
}七、Kinetic Tournamen Tree
(有读者评论问能不能实现 KTT,我们讨论研究后发现是可以的。)
1、介绍
KTT 最初在 2020 年集训队论文中由 EI队长提出。
KTT 用来维护动态区间最大值 问题,其基本思想为将需要维护的信息看作一次函数 ,所有修改都基于函数进行。同时设置阈值,表示维护的答案取值何时发生变化,当修改或查询的信息达到阈值时,暴力重构子树维护答案。
笔者觉得学习 KTT 最好还是从一些具体问题入手。所以我们下文的内容,全部围绕 论文中提到的经典问题 P5693 EI 的第六分块进行展开。
2、信息处理
最大子段和要记录四个信息用线段树维护,信息合并时分类讨论:
- \(lmax = \max(lmax_{ls},sum_{ls}+lmax_{rs})\);
- \(rmax = \max(rmax_{rs},sum_{rs}+rmax_{ls})\);
- \(mx = \max(mx_{ls},mx_{rs},rmax_{ls}+lmax_{rs})\)。
进行动态维护就要用 KTT 了,这是我们的重点内容。
现在每个信息记录的都不是一个具体值,而是一条一次函数 :\(f(x)=kx+b\)。
其中 \(k\) 为最大子段的长度,\(x\) 为变化量,\(f(0)=b\) 为当前维护的具体值。
同时,对于两条函数,记录一个阈值 \(dx\) ,表示当前区间最大值是否在两个函数间进行交替。
3、关于交替阈值
前置知识:人教版八年级下册 19.2.3一次函数与方程、不等式
在对两条函数进行合并取最大值 时,需要知道具体应该何时 选取哪条函数。我们知道应该看函数的交点相对于区间的位置,来对取值情况分类讨论。
交替阈值就干了这样一件事情,维护时记录下何时应该对函数选取进行交替,并只在需要交替时交替,以此优化时间复杂度。
具体地,当区间加 \(q\) 时,函数向上进行了移动,函数的交点相对于区间进行了左右移动。此时我们令阈值 \(dx\) 减小 ,当 \(dx<0\) 时表示此时选取的函数要进行交替了。
具体减少多少呢,由于函数都满足 \(k\ge 1\),所以至少要令 \(dx-=q\)(当然最好是这个数,减多了重构次数就太多了)。
由于同一个区间可能有两个不同的函数进行维护,所以在合并区间时,阈值不仅要对左右区间取最小值,还需要包含当前两条函数的交点。
4、区间及函数合并
笔者个人建议写成重载运算符 形式。
针对函数的操作,有求交点、函数合并、函数移动:
cpp
//struct Func
inline Func operator + (const Func&G) const{//函数合并
return Func(k+G.k,b+G.b);
}
inline ll operator & (const Func&G) const{//求交点
return (G.b-b)/(k-G.k);
}
inline void operator += (const ll&G){//函数向上移动
b += k*G;
}区间合并时,我们在函数操作的基础上分类讨论即可,注意同时维护阈值信息:
cpp
//struct Tree
inline bool operator < (const Func&G) const{
//钦定两条函数的相对位置,方便判断有没有交点
return k==G.k && b<G.b || k<G.k;
}
inline void Merge_lx(Func x,Func y,Tree &tmp) const{//求lmax
if(x<y) swap(x,y);
if(x.b>=y.b) tmp.lx = x;//钦定过了函数位置,此时两条函数没有交点
else tmp.lx = y,tmp.dx = Min(tmp.dx,x&y);
}
//...
inline Tree operator + (const Tree&G) const{//区间合并
Tree tmp;tmp.sum = sum+G.sum; tmp.dx = Min(dx,G.dx);//注意维护阈值信息
Merge_lx(lx,sum+G.lx,tmp);Merge_rx(G.rx,G.sum+rx,tmp);
Merge_mx(G.mx,mx,tmp);Merge_mx(tmp.mx,rx+G.lx,tmp);
return tmp;
}5、修改与重构
区间加按照正常的方式来,唯一不同的是在修改后需要对节点子树进行重构 。
首先第一步肯定是下放标记:
cpp
//struct Tree
inline void operator += (const ll&G){//区间加
lx += G; rx += G; mx += G; sum += G; dx -= G;
}
//
inline void push_down(int p){//正常push_down
if(tag[p]){
tag[p<<1] += tag[p]; tr[p<<1] += tag[p];
tag[p<<1|1] += tag[p]; tr[p<<1|1] += tag[p];
tag[p] = 0;
}
}然后再正常做修改:
cpp
//
inline void update(int l,int r,ll k){
l += P-1; r += P+1;//先push_down
for(int dep=DEP;dep;--dep) push_down(l>>dep),push_down(r>>dep);
while(l^1^r){
if(~l&1) tag[l^1]+=k,tr[l^1]+=k,rebuild(l^1);//别忘了重构
if(r&1) tag[r^1]+=k,tr[r^1]+=k,rebuild(r^1);
l>>=1;r>>=1;
tr[l] = tr[l<<1]+tr[l<<1|1];
tr[r] = tr[r<<1]+tr[r<<1|1];
}
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];
}对于重构,从当前子树的根节点开始一层一层向下递推,直到没有节点需要重构为止:
cpp
//
inline void rebuild(int p){
if(tr[p].dx>=0) return ;
int head = 1,tail = 0;
st[++tail] = p; push_down(p);
while(tail>=head){//模拟压栈
int ttail = tail;
for(int j=tail,pos;j>=head;--j){
pos = st[j]; //看子节点的子树是否需要更新
if(tr[pos<<1].dx<0) st[++tail]=pos<<1,push_down(pos<<1);//注意push_down
if(tr[pos<<1|1].dx<0) st[++tail]=pos<<1|1,push_down(pos<<1|1);
}
head = ttail+1;
}//重新维护
do{ tr[st[tail]]=tr[st[tail]<<1]+tr[st[tail]<<1|1]; } while(--tail);
}6、查询
正常做查询就可以了。
需要注意一点,区间合并时要按照左右顺序进行。
cpp
//
inline ll query(int l,int r){
l += P-1; r += P+1;//先push_down
for(int dep=DEP;dep;--dep) push_down(l>>dep),push_down(r>>dep);
Tree resl,resr;
while(l^1^r){
//注意左右区间的合并顺序
if(~l&1) resl = resl+tr[l^1];
if(r&1) resr = tr[r^1]+resr;
l>>=1;r>>=1;
}
return (resl+resr).mx.b;
}KTT 的基本思路就是这样,将信息转换为函数进行处理,同时维护阈值进行重构。这使得 KTT 有优于分块的复杂度,但同时也对其使用产生了限制。
到现在,能肯定 zkw 线段树基本可以实现递归线段树能做的全部操作了。
一些模板题及代码
放云剪贴板了,会跟随文章更新。
后记
更新日志
笔者目前学识过于浅薄,文章大部分内容是笔者自己的理解,可能有地方讲得不是很清楚。等笔者再学会新东西,会先更新在此文章以及我的博客,然后找时间统一更新。
同时,笔者会经常对文章内容细节和代码块进行修改完善,如果您有什么想法可以提出来,我们一起来解决。作者真的真的是活的!!!
期待您提出宝贵的建议。
鸣谢
《统计的力量》清华大学-张昆玮 /hzwer整理
OIWiki
CSDN 偶耶XJX
Tifa's Blog【洛谷日报 #35】Tifa
洛谷日报 #4 皎月半洒花
NianFeng // EntropyIncreaser //
如需转载,请注明出处。