A - 123233
Problem Statement
You are given a 6 6 6-digit positive integer N N N.
Determine whether N N N satisfies all of the following conditions.
Among the digits of N N N, the digit 1 1 1 appears exactly once.
Among the digits of N N N, the digit 2 2 2 appears exactly twice.
Among the digits of N N N, the digit 3 3 3 appears exactly three times.
Constraints
N N N is an integer satisfying 100000 ≤ N ≤ 999999 100000 \le N \le 999999 100000≤N≤999999.
Input
The input is given from Standard Input in the following format:
N N N
Output
Print Yes if N N N satisfies all the conditions described in the problem statement, and No otherwise, in one line.
Sample Input 1
123233Sample Output 1
Yes123233 123233 123233 satisfies the conditions in the problem statement, so print Yes.
Sample Input 2
123234Sample Output 2
No123234 123234 123234 does not satisfy the conditions in the problem statement, so print No.
Sample Input 3
323132Sample Output 3
YesSample Input 4
500000Sample Output 4
NoSolution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
signed main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
string s;
cin >> s;
int cnt[10] = {0};
for (auto v : s)
cnt[v - '0'] ++;
if (cnt[1] == 1 && cnt[2] == 2 && cnt[3] == 3) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}B - Hurdle Parsing
Problem Statement
Iroha has a sequence of positive integers A = ( A 1 , A 2 , ... , A N ) A = (A_1, A_2, \dots, A_N) A=(A1,A2,...,AN) of length N N N ( N ≥ 1 N \ge 1 N≥1).
She generated a string S S S using A A A as follows:
Start with S = |.
For i = 1 , 2 , ... , N i = 1, 2, \dots, N i=1,2,...,N, perform the following operations in order:
Append A i A_i Ai copies of - to the end of S S S.
Then, append one | to the end of S S S.
Given the generated string S S S, reconstruct the sequence A A A.
Constraints
S S S is a string of length between 3 3 3 and 100 100 100, inclusive, generated by the method in the problem statement.
A A A is a sequence of positive integers of length at least 1 1 1.
Input
The input is given from Standard Input in the following format:
S S S
Output
Print the answer in the following format, with elements separated by spaces in a single line:
A 1 A_1 A1 A 2 A_2 A2 ... \dots ... A N A_N AN
Sample Input 1
|---|-|----|-|-----|Sample Output 1
3 1 4 1 5S = |---|-|----|-|-----| is generated by A = ( 3 , 1 , 4 , 1 , 5 ) A = (3, 1, 4, 1, 5) A=(3,1,4,1,5).
Sample Input 2
|----------|Sample Output 2
10Sample Input 3
|-|-|-|------|Sample Output 3
1 1 1 6Solution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
signed main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
string s;
cin >> s;
int cnt = 0;
for (int i = 1; i < s.size(); i ++)
if (s[i] == '-') cnt ++;
else {
cout << cnt << " ";
cnt = 0;
}
cout << endl;
return 0;
}C - Move Segment
Problem Statement
You are given a string S S S of length N N N consisting of 0 and 1.
Move the K K K-th 1-block from the beginning in S S S to immediately after the ( K − 1 ) (K-1) (K−1)-th 1-block, and print the resulting string.
It is guaranteed that S S S contains at least K K K 1-blocks.
Here is a more precise description.
Let S l ... r S_{l\ldots r} Sl...r denote the substring of S S S from the l l l-th character through the r r r-th character.
We define a substring S l ... r S_{l\ldots r} Sl...r of S S S to be a 1-block if it satisfies all of the following conditions:
S_l = S_{l+1} = \\cdots = S_r = 1
l = 1 l = 1 l=1 or S_{l-1} = 0
r = N r = N r=N or S_{r+1} = 0
Suppose that all 1-blocks in S S S are S l 1 ... r 1 , ... , S l m ... r m S_{l_1\ldots r_1}, \ldots, S_{l_m\ldots r_m} Sl1...r1,...,Slm...rm, where KaTeX parse error: Expected 'EOF', got '&' at position 5: l_1 &̲lt; l_2 < \c....
Then, we define the length N N N string T T T, obtained by moving the K K K-th 1-block to immediately after the ( K − 1 ) (K-1) (K−1)-th 1-block, as follows:
T i = S i T_i = S_i Ti=Si for 1 ≤ i ≤ r K − 1 1 \leq i \leq r_{K-1} 1≤i≤rK−1
T_i = 1 for r K − 1 + 1 ≤ i ≤ r K − 1 + ( r K − l K ) + 1 r_{K-1} + 1 \leq i \leq r_{K-1} + (r_K - l_K) + 1 rK−1+1≤i≤rK−1+(rK−lK)+1
T_i = 0 for r K − 1 + ( r K − l K ) + 2 ≤ i ≤ r K r_{K-1} + (r_K - l_K) + 2 \leq i \leq r_K rK−1+(rK−lK)+2≤i≤rK
T i = S i T_i = S_i Ti=Si for r K + 1 ≤ i ≤ N r_K + 1 \leq i \leq N rK+1≤i≤N
Constraints
1 ≤ N ≤ 5 × 1 0 5 1 \leq N \leq 5 \times 10^5 1≤N≤5×105
S S S is a string of length N N N consisting of 0 and 1.
2 ≤ K 2 \leq K 2≤K
S S S contains at least K K K 1-blocks.
Input
The input is given from Standard Input in the following format:
N N N K K K
S S S
Output
Print the answer.
Sample Input 1
15 3
010011100011001Sample Output 1
010011111000001S S S has four 1-blocks: from the 2nd to the 2nd character, from the 5th to the 7th character, from the 11th to the 12th character, and from the 15th to the 15th character.
Sample Input 2
10 2
1011111111Sample Output 2
1111111110Solution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
signed main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int n, m;
string s;
cin >> n >> m >> s;
std::vector<PII> seg;
int lst = -1;
for (int i = 0; i < n; i ++)
if (s[i] == '1') {
if (lst == -1) lst = i;
} else {
if (lst != -1) seg.push_back({lst, i - 1});
lst = -1;
}
if (~lst) seg.push_back({lst, n - 1});
m --;
for (int i = 0; i <= seg[m - 1].se; i ++)
cout << s[i];
for (int i = 1; i <= seg[m].se - seg[m].fi + 1; i ++)
cout << 1;
for (int i = 1; i < seg[m].fi - seg[m - 1].se; i ++)
cout << 0;
for (int i = seg[m].se + 1; i < n; i ++)
cout << s[i];
cout << endl;
return 0;
}D - Strange Mirroring
Problem Statement
You are given a string S S S consisting of uppercase and lowercase English letters.
We perform the following operation on S S S 1 0 100 10^{100} 10100 times:
First, create a string T T T by changing uppercase letters in S S S to lowercase, and lowercase letters to uppercase.
Then, concatenate S S S and T T T in this order to form a new S S S.
Answer Q Q Q queries. The i i i-th query is as follows:
Find the K i K_i Ki-th character from the beginning of S S S after all operations are completed.
Constraints
S S S is a string consisting of uppercase and lowercase English letters, with length between 1 1 1 and 2 × 1 0 5 2 \times 10^5 2×105, inclusive.
Q Q Q and K i K_i Ki are integers.
1 ≤ Q ≤ 2 × 1 0 5 1 \le Q \le 2 \times 10^5 1≤Q≤2×105
1 ≤ K i ≤ 1 0 18 1 \le K_i \le 10^{18} 1≤Ki≤1018
Input
The input is given from Standard Input in the following format:
S S S
Q Q Q
K 1 K_1 K1 K 2 K_2 K2 ... \dots ... K Q K_Q KQ
Output
Let C i C_i Ci be the answer to the i i i-th query. Print them in a single line, separated by spaces, in the following format:
C 1 C_1 C1 C 2 C_2 C2 ... \dots ... C Q C_Q CQ
Sample Input 1
aB
16
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Sample Output 1
a B A b A b a B A b a B a B A bBefore the operations, S = aB.
After performing the operation once on aB, it becomes aBAb.
After performing the operation twice on aB, it becomes aBAbAbaB.
... \dots ...
After performing the operation 1 0 100 10^{100} 10100 times, S = aBAbAbaBAbaBaBAb...
Sample Input 2
qWeRtYuIoP
8
1 1 2 3 5 8 13 21Sample Output 2
q q W e t I E QSample Input 3
AnUoHrjhgfLMcDIpzxXmEWPwBZvbKqQuiJTtFSlkNGVReOYCdsay
5
1000000000000000000 123456789 1 987654321 999999999999999999Sample Output 3
K a A Z LSolution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
int q;
string s;
char change(char x) {
if (x >= 'A' && x <= 'Z') return x - 'A' + 'a';
else return x - 'a' + 'A';
}
signed main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> s >> q;
while (q -- ) {
int x;
cin >> x, x --;
if (__builtin_popcountll(x / s.size()) & 1) cout << change(s[x % s.size()]) << " ";
else cout << s[x % s.size()] << " ";
}
cout << endl;
return 0;
}E - 1D Bucket Tool
Problem Statement
There are N N N cells in a row, numbered 1 1 1 to N N N.
For each KaTeX parse error: Expected 'EOF', got '&' at position 10: 1 \leq i &̲lt; N, cells i i i and i + 1 i+1 i+1 are adjacent.
Initially, cell i i i is painted with color i i i.
You are given Q Q Q queries. Process them in order. Each query is of one of the following two types.
1 x c: Repaint the following to color c c c: all reachable cells reachable from cell x x x by repeatedly moving to an adjacent cell painted in the same color as the current cell.
2 c: Print the number of cells painted with color c c c.
Constraints
1 ≤ N ≤ 5 × 1 0 5 1 \leq N \leq 5 \times 10^5 1≤N≤5×105
1 ≤ Q ≤ 2 × 1 0 5 1 \leq Q \leq 2 \times 10^5 1≤Q≤2×105
In queries of the first type, 1 ≤ x ≤ N 1 \leq x \leq N 1≤x≤N.
In queries of the first and second types, 1 ≤ c ≤ N 1 \leq c \leq N 1≤c≤N.
There is at least one query of the second type.
All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N Q Q Q
q u e r y 1 \mathrm{query}_1 query1
⋮ \vdots ⋮
q u e r y Q \mathrm{query}_Q queryQ
Each query is given in one of the following two formats:
1 1 1 x x x c c c
2 2 2 c c c
Output
Let q q q be the number of queries of the second type. Print q q q lines.
The i i i-th line should contain the answer to the i i i-th such query.
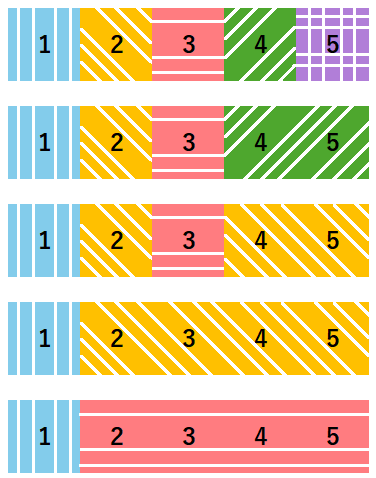
Sample Input 1
5 6
1 5 4
1 4 2
2 2
1 3 2
1 2 3
2 3Sample Output 1
3
4The queries recolor the cells as shown in the figure.
Solution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int N = 5E5 + 10;
int n, q;
int l[N], r[N], sz[N], col[N], ans[N];
int findl(int x) {
if (l[x] != x) l[x] = findl(l[x]);
return l[x];
}
int findr(int x) {
if (r[x] != x) r[x] = findr(r[x]);
return r[x];
}
void merge(int a, int b) {
int u1 = findl(a), u2 = findl(b);
int v1 = findr(a), v2 = findr(b);
if (u1 != u2) {
l[u2] = u1, r[v1] = v2, sz[v2] += sz[v1];
}
}
signed main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> n >> q;
for (int i = 1; i <= n; i ++)
l[i] = r[i] = i, sz[i] = 1, col[i] = i, ans[i] = 1;
while (q -- ) {
int op, x, c;
cin >> op;
if (op == 1) {
cin >> x >> c;
ans[col[findr(x)]] -= sz[findr(x)], ans[c] += sz[findr(x)];
if (col[findr(findl(x) - 1)] == c) merge(findl(x) - 1, x);
if (col[findr(findr(x) + 1)] == c) merge(x, findr(x) + 1);
col[findr(x)] = c;
} else {
cin >> c;
cout << ans[c] << endl;
}
}
return 0;
}F - Exchange Game
Problem Statement
Takahashi and Aoki will play a game using cards with numbers written on them.
Initially, Takahashi has N N N cards with numbers A 1 , ... , A N A_1, \ldots, A_N A1,...,AN in his hand, Aoki has M M M cards with numbers B 1 , ... , B M B_1, \ldots, B_M B1,...,BM in his hand, and there are L L L cards with numbers C 1 , ... , C L C_1, \ldots, C_L C1,...,CL on the table.
Throughout the game, both Takahashi and Aoki know all the numbers on all the cards, including the opponent's hand.
Starting with Takahashi, they take turns performing the following action:
Choose one card from his hand and put it on the table. Then, if there is a card on the table with a number less than the number on the card he just played, he may take one such card from the table into his hand.
The player who cannot make a move first loses, and the other player wins. Determine who wins if both players play optimally.
It can be proved that the game always ends in a finite number of moves.
Constraints
1 ≤ N , M , L 1 \leq N, M, L 1≤N,M,L
N + M + L ≤ 12 N + M + L \leq 12 N+M+L≤12
1 ≤ A i , B i , C i ≤ 1 0 9 1 \leq A_i, B_i, C_i \leq 10^9 1≤Ai,Bi,Ci≤109
All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N M M M L L L
A 1 A_1 A1 ... \ldots ... A N A_N AN
B 1 B_1 B1 ... \ldots ... B M B_M BM
C 1 C_1 C1 ... \ldots ... C L C_L CL
Output
Print Takahashi if Takahashi wins, and Aoki if Aoki wins.
Sample Input 1
1 1 2
2
4
1 3Sample Output 1
AokiThe game may proceed as follows (not necessarily optimal moves):
Takahashi plays 2 2 2 from his hand to the table, and takes 1 1 1 from the table into his hand. Now, Takahashi's hand is ( 1 ) (1) (1), Aoki's hand is ( 4 ) (4) (4), and the table cards are ( 2 , 3 ) (2,3) (2,3).
Aoki plays 4 4 4 from his hand to the table, and takes 2 2 2 into his hand. Now, Takahashi's hand is ( 1 ) (1) (1), Aoki's hand is ( 2 ) (2) (2), and the table cards are ( 3 , 4 ) (3,4) (3,4).
Takahashi plays 1 1 1 from his hand to the table. Now, Takahashi's hand is ( ) () (), Aoki's hand is ( 2 ) (2) (2), and the table cards are ( 1 , 3 , 4 ) (1,3,4) (1,3,4).
Aoki plays 2 2 2 from his hand to the table. Now, Takahashi's hand is ( ) () (), Aoki's hand is ( ) () (), and the table cards are ( 1 , 2 , 3 , 4 ) (1,2,3,4) (1,2,3,4).
Takahashi cannot make a move and loses; Aoki wins.
Sample Input 2
4 4 4
98 98765 987654 987654321
987 9876 9876543 98765432
123 12345 1234567 123456789Sample Output 2
TakahashiSample Input 3
1 1 8
10
10
1 2 3 4 5 6 7 8Sample Output 3
AokiSolution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
int N, M, L;
int card[12], TH[12];
char dp[531441][2];
char DP(int mask, int turn) {
if (dp[mask][turn]) return dp[mask][turn];
dp[mask][turn] = 1;
for (int i = 0; i < N + M + L; i ++)
if (mask / TH[i] % 3 == turn) {
if (DP(mask - TH[i] * turn + TH[i] * 2, turn ^ 1) == 1)
dp[mask][turn] = 2;
if (dp[mask][turn] == 2) break;
for (int j = 0; j < N + M + L; j ++)
if (mask / TH[j] % 3 == 2 && card[j] < card[i] && DP(mask - (TH[i] - TH[j]) * turn + (TH[i] - TH[j]) * 2, turn ^ 1) == 1)
dp[mask][turn] = 2;
if (dp[mask][turn] == 2) break;
}
return dp[mask][turn];
}
signed main() {
std::cin >> N >> M >> L;
TH[0] = 1;
for (int i = 0; i < N + M + L; i ++)
std::cin >> card[i], TH[i + 1] = TH[i] * 3;
if (DP((TH[N + M] - TH[N] >> 1) + (TH[N + M + L] - TH[N + M]), 0) == 2) printf("Takahashi");
else printf("Aoki");
return 0;
}G - Another Shuffle Window
Problem Statement
You are given a permutation P P P of ( 1 , 2 , ... , N ) (1,2,\dots,N) (1,2,...,N) and an integer K K K.
Find the expected value, modulo 998244353 998244353 998244353, of the inversion number of P P P after performing the following operation:
First, choose an integer i i i uniformly at random between 1 1 1 and N − K + 1 N - K + 1 N−K+1, inclusive.
Then, shuffle P i , P i + 1 , ... , P i + K − 1 P_i, P_{i+1}, \dots, P_{i+K-1} Pi,Pi+1,...,Pi+K−1 uniformly at random.
What is the inversion number? The inversion number of a sequence (A_1, A_2, \\dots, A_N) is the number of integer pairs (i, j) satisfying 1 \\le i \< j \\le N and A_i \> A_j. What does "expected value modulo 998244353" mean? It can be proved that the sought expected value is always rational. Under the constraints of this problem, when this value is represented as an irreducible fraction \\frac{P}{Q}, it can also be proved that Q \\not\\equiv 0 \\pmod{998244353}. Thus, there is a unique integer R satisfying R \\times Q \\equiv P \\pmod{998244353}, \\ 0 \\le R \< 998244353. Report this integer R. ## Constraints
All input values are integers.
1 ≤ K ≤ N ≤ 2 × 1 0 5 1 \le K \le N \le 2 \times 10^5 1≤K≤N≤2×105
P P P is a permutation of ( 1 , 2 , ... , N ) (1,2,\dots,N) (1,2,...,N).
Input
The input is given from Standard Input in the following format:
N N N K K K
P 1 P_1 P1 P 2 P_2 P2 ... \dots ... P N P_N PN
Output
Print the answer in one line.
Sample Input 1
4 2
1 4 2 3Sample Output 1
166374061The operation changes the permutation P P P into the following:
( 1 , 4 , 2 , 3 ) (1,4,2,3) (1,4,2,3) ... probability 1 / 2 1/2 1/2
( 4 , 1 , 2 , 3 ) (4,1,2,3) (4,1,2,3) ... probability 1 / 6 1/6 1/6
( 1 , 2 , 4 , 3 ) (1,2,4,3) (1,2,4,3) ... probability 1 / 6 1/6 1/6
( 1 , 4 , 3 , 2 ) (1,4,3,2) (1,4,3,2) ... probability 1 / 6 1/6 1/6
The expected value of the inversion number is 2 × 1 2 + 3 × 1 6 + 1 × 1 6 + 3 × 1 6 = 13 6 \displaystyle 2 \times \frac{1}{2} + 3 \times \frac{1}{6} + 1 \times \frac{1}{6} + 3 \times \frac{1}{6} = \frac{13}{6} 2×21+3×61+1×61+3×61=613.
13 6 \displaystyle \frac{13}{6} 613 modulo 998244353 998244353 998244353 is 166374061 166374061 166374061, so print this number.
Sample Input 2
1 1
1Sample Output 2
0Sample Input 3
10 6
7 4 10 5 6 1 8 2 3 9Sample Output 3
499122200Solution
具体见文末视频。
Code
cpp
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
void exgcd(int a, int b, int &x, int &y) {
if (!b) { x = 1, y = 0; return; }
exgcd(b, a % b, y, x);
y -= a / b * x;
}
template <int mod>
struct modint {
int v;
int norm(const int &x) { return x < 0 ? x + mod : x; }
int get_mod() { return mod; }
modint() : v(0) {}
modint(int x) : v(norm(x % mod)) {}
modint operator-() const {
modint res;
return res.v = -v;
}
bool operator== (const modint &x) { return v == x.v; }
bool operator< (const modint &x) { return v < x.v; }
bool operator> (const modint &x) { return v > x.v; }
modint operator+= (const modint &x) { return v = (v + x.v) % mod; }
modint operator-= (const modint &x) { return v = norm(v - x.v); }
modint operator*= (const modint &x) { return v = v * x.v % mod; }
modint operator/= (const modint &x) {
int a, b;
exgcd(x.v, mod, a, b);
return v = v * norm(a % mod) % mod;
}
modint operator+ (const modint &x) { return (v + x.v) % mod; }
modint operator- (const modint &x) { return norm(v - x.v); }
modint operator* (const modint &x) { return v * x.v % mod; }
modint operator/ (const modint &x) {
int a, b;
exgcd(x.v, mod, a, b);
return v * norm(a % mod) % mod;
}
modint operator+= (const int &x) { return v = (v + x) % mod; }
modint operator-= (const int &x) { return v = norm(v - x); }
modint operator*= (const int &x) { return v = v * x % mod; }
modint operator/= (const int &x) {
int a, b;
exgcd(x, mod, a, b);
return v = v * norm(a % mod) % mod;
}
modint operator^= (int x) {
int res = 1, a = v;
while (x) {
if (x & 1) res = res * a % mod;
a = a * a % mod;
x >>= 1;
}
return res;
}
modint operator+ (const int &x) { return (v + x) % mod; }
modint operator- (const int &x) { return norm(v - x); }
modint operator* (const int &x) { return v * x % mod; }
modint operator/ (const int &x) {
int a, b;
exgcd(x, mod, a, b);
return v * norm(a % mod) % mod;
}
modint operator^ (int x) {
int res = 1, a = v;
while (x) {
if (x & 1) res = res * a % mod;
a = a * a % mod;
x >>= 1;
}
return res;
}
friend istream& operator>> (istream &in, modint &x) {
in >> x.v;
return in;
}
friend ostream& operator<< (ostream &out, modint &x) {
out << x.v;
return out;
}
};
using Mint = modint<998244353>;
Mint to_Mint(int x) {
Mint res(x);
return res;
}
std::vector<Mint> fact, infact, inv;
void prework(int n) {
fact.resize(n + 1, 1), infact.resize(n + 1, 1);
for (int i = 1; i <= n; i ++)
fact[i] = fact[i - 1] * i, infact[i] = infact[i - 1] / i;
}
Mint C(int n, int m) {
return fact[n] * infact[m] * infact[n - m];
}
Mint A(int n, int m) {
return fact[m] * C(n, m);
}
signed main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
int n, m;
cin >> n >> m;
std::vector<int> P(n);
for (int i = 0; i < n; i ++)
cin >> P[i];
std::vector<int> cnt(n + 1), inv(n);
std::vector<int> tot(n + 1);
int ans = 0;
for (int i = 0; i < n; i ++) {
if (i) inv[i] = inv[i - 1];
if (i >= m) {
for (int j = P[i - m]; j; j -= (j & -j)) inv[i] -= cnt[j];
for (int j = P[i - m]; j <= n; j += (j & -j)) cnt[j] --;
inv[i] ++;
}
for (int j = P[i]; j; j -= (j & -j)) inv[i] -= cnt[j];
for (int j = P[i]; j <= n; j += (j & -j)) cnt[j] ++;
inv[i] += min(m - 1, i);
for (int j = P[i]; j <= n; j += (j & -j)) ans += tot[j];
for (int j = P[i]; j; j -= (j & -j)) tot[j] ++;
}
// for (int i = 0; i < n; i ++) cout << inv[i] << " ";
// cout << endl;
Mint res = 0;
for (int i = m - 1; i < n; i ++) {
res += (to_Mint(ans - inv[i]) + to_Mint(m * (m - 1)) / 4) / (n - m + 1);
}
cout << res << endl;
return 0;
}视频题解
AtCoder Beginner Contest 380(A ~ G 题讲解)
最后祝大家早日