
🏡作者主页:点击!
🤖编程探索专栏:点击!
⏰️创作时间:2024年11月15日20点12分

神秘男子影,
秘而不宣藏。
泣意深不见,
男子自持重,
子夜独自沉。
论文链接
对比学习
对比学习是为了在不关注样本全部细节的情况下,训练一个Encoder将样本转化为表征(representation,比如用一个编码器将数据编码成高维向量,就可以将得到的向量称为是数据的representation),使得representation包含了更显著的、重要的、有区分度的特征,学到这样的表示之后,用来帮助提升下游任务的性能。
对比学习的关键方法是根据对数据的理解生成正负训练样本对。模型需要学习一个函数,使得两个正样本具有较高的相似度分数,两个负样本具有较低的相似度分数 。因此,适当的样本生成对于确保模型学习数据的底层特征/结构至关重要。
Encoder可以将高维数据压缩到更紧凑 的潜在嵌入空间中进行编码的表示以学习对(高维)信号不同部分之间的底层共享信息,其丢弃了更局部的低级信息和噪声更容易建模。但是预测高维数据的挑战之一是均方误差和交叉熵等单峰损失不是很有用,如果直接建模源数据和特征的复杂关系导致除了模型计算量很大之外,提取 x 和 c 之间的共享信息可能不是最佳的。(例如,图像可能包含数千位信息,而类标签等高级潜在变量包含的信息要少得多(1024 个类别为 10 位)),我们就需要一个强大有效而精炼的Encoder编码器。
但是对于一个encoder来说,怎么样的encoder是好的encoder呢?
autoencoder的训练过程中要求encoder作用过后得到的latent vector被decoder解码后得到的新的matrix和raw matrix的reconstruction error尽可能小,更好的可解释性,更强的代表性和区分度。
所谓区分度,举个例子说明:有三个样本组成的集合{x,x+,x-}, x+ 表示和 x 相似的样本, x- 表示和 x 不相似的样本,"区分度"意味着,x 的representation和 x+ 的representation要较为相似,而 x 的representation和 x- 的representation要较不相似,那样的representation就是有区分度的。
那么如何去判断encoder编码器足够好呢?
这应该就是Contrastive对比学习的思路,我们通过引入一个Discriminator(判别器)来判断编码好坏,这里我们以Discriminator(判别器)为二分类判别器:
如下图,首先我们把原来的image数据和编码后的latent vector构建数据集,例如用(Xi, yi),其中yi是Xi经过encoder后编码的latent vector。我们训练Discriminator,在面对(Xi,yi)告诉discriminator这是positive sample,你该给它高分(1分),然后我们把所有样本(常常是一个batch里的)和与之对应编码器编码的latent vector打乱,比如我们把(Xi,yj)配对放进discriminator,告诉discriminator,这是negetive sample, 应该给它们0分。
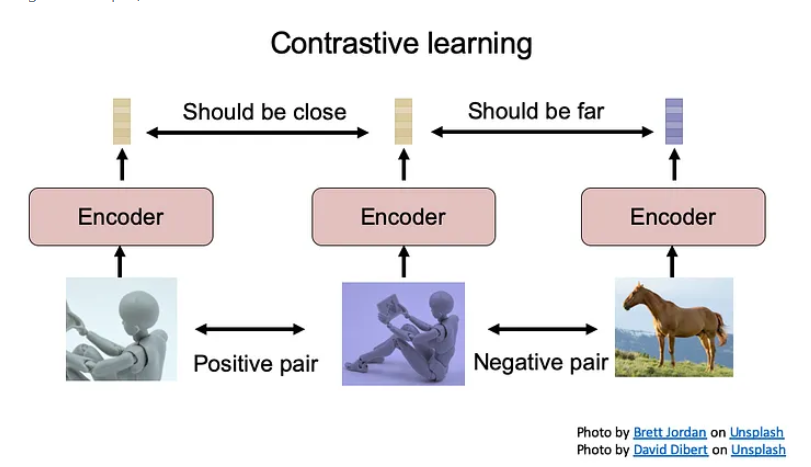
训练好一部分数据后,我们拿一些discriminator没见过的组给它,让discriminator去做二分类,判断输入的(X,y)是不是对应的raw data和latent vector。如果discriminator的识别准确率很高,说明编码所编码的特征是具有分辨度的,否则说明我们很难将encoder学到的latent vectors分开,也就是说这些latent vector是不够具有代表性的。
这里讲这个例子是为了提到这种"把encoder好不好的问题转换为encoding出来的vector和原数据配对后 真假样本能不能被一个分类器分开"的思路,即通过模型来验证 ,我们认为好的latent vector能让classifier比较容易地把正确的latent vector和随机的latent vector 分开。
按照上面的思路,我们来理解一下对比学习的目标。


参考:
https://blog.csdn.net/sinat_34604992/article/details/108385380
CPC 奠基之作
CPC是谷歌 DeepMind团队2019年发布的一篇论文《Representation Learning with Contrastive Predictive Coding 》。改论文提出了一种通用 的无监督学习方法 ------ 一个用于提取紧凑潜在表示以编码对未来观察的预测的框架,从高维数据中提取有用的表示,称之为对比预测编码(Contrastive Predictive Coding)。所得模型------对比预测编码(CPC)------应用于广泛不同的数据模态、图像、语音、自然语言和强化学习,并表明相同的机制 可以学习这些领域中每个领域的有趣的高级信息 ,其性能优于其他方法。
核心思想
模型思想重点在于representation learning(找到raw data的好的representation vector(也叫hidden vector/ latent vector),并希望这个representation有很好的predictive的能力。)
我们根据Contrastive的对比学习思想,原文的Discriminator判别器的作用是用于使得Encode编码的latent vector满足时序特征,并尽可能保留原始信息更多信息,具体来说原文Discriminator判别器采用的模型是预测模型(自回归)来验证特征 。通过输入过去时刻z(t-1)、z(t-2)、z(t-3)、z(t-4) 的编码特征输入到自回归模型后得到的预测值c(t)经过变换,可以与未来时刻z(t+1)、z(t+2)、z(t+3)、z(t+4)的编码特征尽量的接近。即,c(t)通过一些变换后,可以很好的用来重构未来的特征z(t+k)。
在时间序列和高维建模中,自回归模型使用下一步预测的方法利用了信号的局部平滑度 。当进一步预测未来时,共享信息量会变得更低,模型需要推断出更多的全局结构 。这些跨越许多时间步骤的"慢特征"(通用特征)通常更有趣(例如,语音中的音素和语调、图像中的对象或书籍中的故事情节)。
我们首先看预测编码流程架构如下图(音频为例输入,原文对图像、文本和强化学习使用相同的设置)。首先Encoder将输入的观测序列 xt 映射到潜在表示序列 zt = Encoder(xt),并将 论文里是一般性地用 gar 来表示这个可以做预测的有回归性质的model,通常大家会用非线性模型或者循环神经网络。
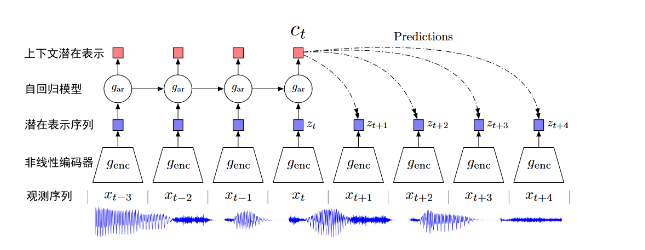
我们用t时刻及其之前的若干时刻输入这个回归模型,自回归模型将总结潜在空间中的所有 z≤t时刻的编码特征并生成上下文潜在表示 ct = gar(z≤t),即涵盖了对过去信息的memory的输出ct。
此时我们希望ct是足够好的且具有预测性质的,那么如何评价它好不好呢?
我们可以通过用ct去预测之后k个时刻的latent vector(k是我们感兴趣的预测的步长)这里记作zt+1,zt+2,...,zt+kz t +1,z t +2,...,z t +k, 然后我们希望 z^t+i (预测的latent vector)和 zt+i (真实的 xt+i 的latent vector)尽可能相似。论文采用直接用使用简单的对数双线性模型对ct进行变换,通过 W1,W2,...,Wk 乘以 ct 做的预测,
fk(x)是z(t+k)和c(t)的相似性度量函数,可以是函数形式、可以是内积、也可以是余弦距离。z(t+k)是t时刻起,未来第k帧的潜在特征,每一个k都对应了一个fk(x)。xj∈Xn(n=1,2,3...N)参与loss计算的这个N个样本中,有1个正样本z(t+k),和N-1个负样本,其中负样本是随机从其他时刻采样的值。整个损失函数的目的是使z(t+k)跟[W(k)c(t)]的相似度尽量的高,跟其他负样本的相似度尽量的低,这样loss才能尽可能的小。
然后用向量内积来衡量相似度。(也可以用非线性网络或循环神经网络)
这样就得到了论文所提出了的相似度函数

其中 fk()表示计算 ct 的预测和 xt+k (真实的未来值)符不符合。
那么得到了相似度函数,我们要如何评价总体的特征编码效果好不好以设置损失函数呢?
原论文提出了用了正样本分数分布与负样本分数比值来进行评价,公式: \\frac {p(x_ {t+k\|ct})}{p(x_ {t+k})}
假设给定了选取X={x1,x2,...,xN}共N个随机样本,包含了一个是来自于p(xt+k∣ct)p (xt +k ∣ct ) 的正样本 ,和其他来自proposal distribution(提议分布)p(xt+k)p (xt +k)的N-1个负样本negative sample(noise sample)
这个分布表示了模型编码的分数好坏,模型编码效果越好分数比值的值越大(越靠近1),而相似度函数中则是计算分数的,那么有公式 f_ {k} ( x_ {t+k} , c_ {t} ) \\infty \\frac {p(x_ {t+k\|ct})}{p(x_ {t+k})} ,即正样本的相似度函数是和 \\frac {p(x_ {t+k\|ct})}{p(x_ {t+k})} 是正相关的,也就是说fk()值越大相似度越大,预测效果越好,那么模型特征表征也就越好,那么设计损失函数便是将 \\frac {p(x_ {t+k\|ct})}{p(x_ {t+k})} 最大化,这样我们就得到了最终的损失函数表达如下(Noise-Contrastive Estimation(NCE) Loss, 在这篇文献里定义为InfoNCE)
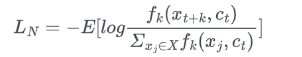
其中分母是负样本的分数之和(从分布中选取全部的负样本),最终的对数分布比期望越小时, \\frac {p(x_ {t+k\|ct})}{p(x_ {t+k})} 越大。
看到一个很好的思路,这里引用以下:
为什么负采样是在整段序列上进行采样,那样不是会采样到窗口内的单词吗?
我们知道,正样本来源于 t 时刻的一定窗口内的单词,按照正常思路,负样本应该来源于窗口以外的单词,这里有一个问题,假如一段长的序列,窗口内的单词在窗口外也出现了(比如"你,我"等常见词),这仍然不能避免负采样取到窗口内单词。所以作者直接在整段序列上进行负采样,负样本来源于整段序列的分布,正样本来源于窗口内单词的分布,这样做是为了让模型在给定一个context情况下判断某个样本来源于窗口内分布还是整段序列的噪声分布,也就是只需要模型可以区分窗口内分布和整段序列的噪声分布,这其实是一种退而求其次的方法,因为负采样本身就是为了避免在整个词典上进行softmax的开销过大问题,假如纠结负采样会采样到真实样本,那么干脆直接不要负采样,就在整个词典上进行正样本与其他单词的区分就好了(这样做显然是没必要的)。所以,CPC论文的负采样就直接在整段序列上进行采样,当序列长度足够长,且负采样的次数足够多时,这么做是能够很好的模拟真实噪音分布的,而CPC的论文实验部分也证明了这一点。
最终编码器和自回归模型都将经过训练,将共同优化基于 NCE 的损失。其中将通过自回归模型的训练来反向使优化编码器编码。
我们再来总结一下,为了训练得到有效的Encoder编码器,论文引入了一个Decriminator 自回归模型来验证编码好坏,其中使用了相似度函数和正负样本分数比来作为评价指标,通过同时训练自回归模型和编码器最终得到良好的Representation learning 表示学习。
算法实践
我们在训练好模型之后,可以使用的训练好encoder部分或者encoder+自回归模型提取数据的特征用于不同的下游任务,或者在模型后面串接一个小型的微调网络,然后通过cross entropy或者CTC等任务的损失函数即可实现下游任务的训练。
算法代码实现库:
算法的 Keras 实现:https://github.com/davidtellez/contrastive-predictive-coding
Github复现主题系列:https://github.com/topics/contrastive-predictive-coding
参考文章:
非常感谢这篇文章,给我了很大的思路和帮助:https://zhuanlan.zhihu.com/p/129076690
https://blog.csdn.net/sinat_34604992/article/details/108385380
成功的路上没有捷径,只有不断的努力与坚持。如果你和我一样,坚信努力会带来回报,请关注我,点个赞,一起迎接更加美好的明天!你的支持是我继续前行的动力!"
"每一次创作都是一次学习的过程,文章中若有不足之处,还请大家多多包容。你的关注和点赞是对我最大的支持,也欢迎大家提出宝贵的意见和建议,让我不断进步。"
神秘泣男子
