想了解本质的直接看第二点
一、Logistic回归算法
-
Logistic 回归算法,又叫做逻辑回归算法,或者 LR 算法(Logistic Regression),它是一个分类算法,主要用来解决的是二分类问题,比图像识别、垃圾邮件处理、预测天气、疾病诊断等。
-
逻辑回归算法是通过估计事件发生的概率来预测类别,并根据这个概率决定最终的分类结果。
2、Sigmoid函数
-1.逻辑回归的核心思想是使用一个 Sigmoid 函数来将线性组合的输出映射到 [0, 1] 区间内,表示某一类事件发生的概率。该函数图像的数学表达式如下:
-2. Sigmoid 函数的形式为:其取值范围在 (0,1) 之间,当 x=0 时,该函数的取值为 0.5,随着 x 的增大,对应的函数值将逼近于 1,称为正例;而随着 x 的减小,其函数值将逼近于 0,称为负例。根据中间的 0.5 作为分界线把数据分为二类,即当 y > 0.5 属于一类,当 y < 0.5 属于一类 。 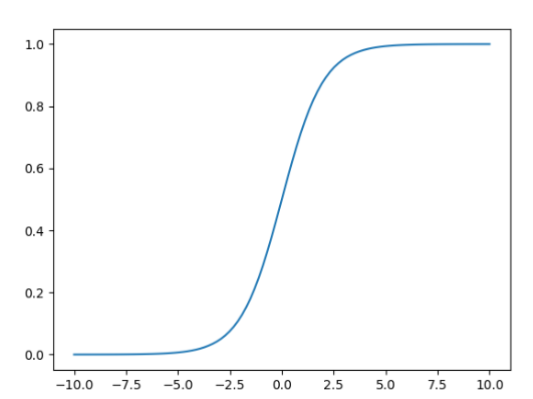
- 3.二分类问题一般都是通过 0 和 1 表示不同的类别,所以逻辑回归二分类问题会把正例设置为 1,负例设置为 0。
3、损失函数
- 1.总体:
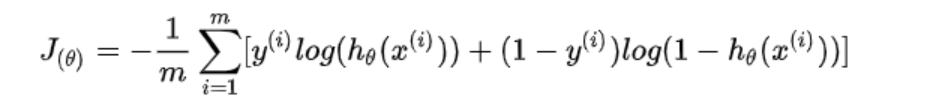
-
分段:
-
当 y_i=1 时,损失函数简化为 -log(h_\theta(x)) ,这意味着如果真实标签为正类 1,则损失函数惩罚的是模型预测为正类的概率
-
当 y_i=0 时,损失函数简化为 -log(1-h_\theta(x)) ,这意味着如果真实标签为负类 0,则损失函数惩罚的是模型预测为负类的概率
二,正篇开始!!!:
1.为什么逻辑回归解决二分类问题
假设对于一个二分类数据集,我们以一个点为一个样本,class1为正类我们给label为1,class2的label则为0,如下:
python
# 数据集定义
class1_points = np.array([[1.9, 1.2],
[1.5, 2.1],
[1.9, 0.5],
[1.5, 0.9],
[0.9, 1.2],
[1.1, 1.7],
[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],
[3.7, 2.9],
[3.2, 2.6],
[1.7, 3.3],
[3.4, 2.6],
[4.1, 2.3],
[3.0, 2.9]])如果我们把两个数据集粘在一起
python
all_data = np.vstack((class1_points, class2_points))我们可以用这个all_data做线性回归,但是!
class1是一类,class2是一类,如果我们用all_data做数据集,他们的权重w必然不可能拟合的完美,甚至会很差。可以想象两个完全不同的族群,一个是各种各样的植物,一个是自然界的动物,哪怕我们给出再多的特征,拟合的那条回归线也必然不准确。所以我们需要w1,w2两个权重来进行拟合。w1针对class1,w2针对class2,加上我们的偏移量b,于是我们得到了第一个式子。
可以看出这是具有线性关系的式子,或许我们将某种植物或者某种动物的特征带入方程,通过线性回归,梯度下降,我们不难得到一个不知道结果是植物,还是动物的生物相关的权重。也就是说通过线性拟合,我们只能得到一个连续的得分,而不是类别。
那有没有什么办法能使这个式子能够判断他的类别呢?比如,带入式子,我们能够知道他接近0,就是植物,接近1就是动物。
当我提到0和1你是否想到了概率P
如果能让 P = w1x1+w2x2+ b 这是不是就能够解决这个问题呢。
显然这是不可能的,因为 line是线性的(二维平面的直线),他是上限,下限都是无穷!!!
所以我们想办法让line的取值有一个范围!!!0-1
2.逻辑回归的建模过程
如果你看了前面的内容,你是否想到了sigmodi函数,没错,使用sigmoid函数。
假设line = z,我们带入sigmoid函数得到
python
def sigmoid(z):
return 1 / (1 + np.exp(-z))看到这你是不是很高兴 如果我们让 概率 P = sigmoid(line)
这是不是就完成了我们前面的设想,但是想法很美好,这只是我们的假设,没有任何依据,那有没有什么办法能够得到这个结果呢?
我们无法让P 直接等于 sigmoid(z),那我们能否通过一下数学思想或者建模思想,得到这个式子呢?
有的。
在数学中 某一事件的概率=P ,他的反事件=1-P
那么概率比 =
因为前面sigmoid里面涉及到e的x次方,我们继续联想到对数几率。
前面我们提到我们无法直接让
P = sigmoid(line)
那么我们能否让 对数几率 = line
没错。
假设
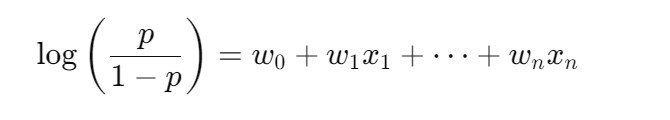
注意:左边不是概率,而是一个可以取正也可以取负的"线性空间"(所以右边可以用线性函数来表达)。
我们要是能够通过数学计算得到 P = sigmoid(line) 那么是不是说明我们的假设成立!!!
想必机智如你已经猜到了。
我们把行向量w1,w2换算成矩阵W的转置,方便我们计算。

于是我们得到了
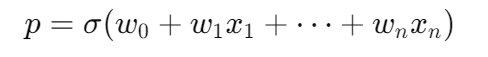
总结:
1**.sigmoid 函数只是一个"工具"------它负责把输入压缩到 (0,1) 之间**,从而可以解释为"概率"。
2.这是一种建模假设 ,它的出发点是可解释性 + 可计算性 。我们在做统计建模/机器学习时,经常需要先假设一种形式,然后用数据去验证它是不是"够好"。
3.线性函数 + sigmoid = 概率
在深度学习中,我们把这种函数称为激活函数。
回到我们前面提出的class1,class2
模型会尝试找到一组参数 (w1,w2),(虽然式子中包含w0,不影响)
目的是让下面这个式子输出 接近于真实概率:
p=σ(w0+w1x1+w2x2)p = \sigma(w_0 + w_1x_1 + w_2x_2)p=σ(w0+w1x1+w2x2)
例如:
-
如果输入是 (1.9, 1.2) → p ≈ 0(属于 class1 的概率比较大)
-
如果输入是 (3.2, 3.2) → p ≈ 1(属于 class2 的概率比较大)
那么决策边界是上面,没错,符合概率论里的是想法 阈值 threshold = 0.5
决策边界就是 p=0.5 的那条线:
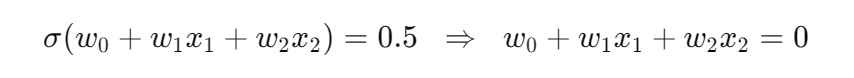
注意它就是一条直线
(所以逻辑回归本质上是一个"线性可分的模型")
总结:逻辑回归 = 假设 log-odds 与特征线性 → 用 sigmoid 转成概率 → 用样本学习参数
3.损失函数的推导
前面我们解释了为什么逻辑回归解决二分类问题,以及是如何把线性映射到概率来判断类别的。
下面我们有了这个模型,就可以来计算模型的损失函数了。
模型:
对于每个样本i:
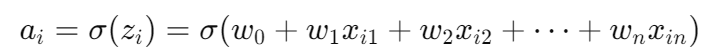
- ai= 模型预测为 1 的概率
注意:逻辑回归模型本身被设计成 "输出 = 属于正类(1)的概率"
- yi∈{0,1}= 样本真实标签
如果 yi=1,概率就是 ai,如果 yi=0i=0,概率就是 1−ai统一起来得到下面的式子
即每个样本的概率可以写成:
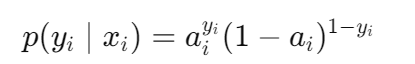
假设样本独立,总似然函数:
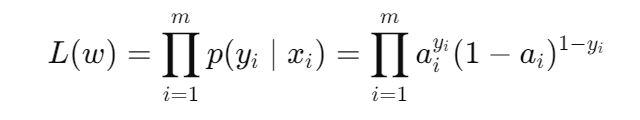
取对数方便求导:
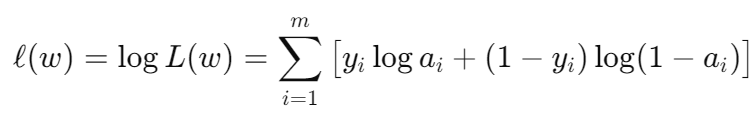
在训练中通常把最大化对数似然问题改成最小化负对数似然:
"可信度"就是我们前面说的似然(likelihood)。
所以我们把 "似然越大越好"
转换成 "损失越小越好"
于是就用 "负对数似然" 作为损失函数。
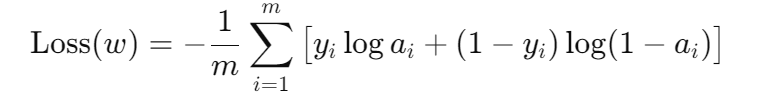
我们之所以把它当成损失函数,是因为它直接衡量 模型对真实标签的"概率支持度" ,
真实标签出现的概率越大 → 模型越好 → 损失越小,
所以它自然就成为一个合乎直觉的"损失指标"。
4.梯度下降法求最佳参数
有了损失函数就和线性回归一下,对各个参数求导就可以进行梯度下降了,这里就不过多赘述了,对于这个loss记得链式求导就可以了,如果有需要的可以看up往期内容。下面给出一个已经写好的代码方便理解。
python
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
def func1():
# 数据集定义
class1_points = np.array([[1.9, 1.2],
[1.5, 2.1],
[1.9, 0.5],
[1.5, 0.9],
[0.9, 1.2],
[1.1, 1.7],
[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],
[3.7, 2.9],
[3.2, 2.6],
[1.7, 3.3],
[3.4, 2.6],
[4.1, 2.3],
[3.0, 2.9]])
all_data = np.vstack((class1_points, class2_points))
X1 = all_data[:, 0]
X2 = all_data[:, 1]
y = np.array([1] * len(class1_points) + [0] * len(class2_points))
# 定义线性函数
def line_func(w1, w2, b):
return w1 * X1 + w2 * X2 + b
# 定义sigmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 定义损失函数
def loss_func(a):
return -np.mean(y * np.log(a) + (1 - y) * np.log(1 - a))
# 训练参数
epochs = 100000
lr = 0.01
w1, w2, b = 0.1, 0.1, 0
# 训练过程
for _ in range(epochs):
z = line_func(w1, w2, b)
a = sigmoid(z)
# 计算梯度
deda = (a - y) / (a * (1 - a))
dadz = a * (1 - a)
dzdw1 = X1
dzdw2 = X2
dzdb = 1
g_w1 = np.mean(deda * dadz * dzdw1)
g_w2 = np.mean(deda * dadz * dzdw2)
g_b = np.mean(deda * dadz * dzdb)
# 更新参数
w1 -= lr * g_w1
w2 -= lr * g_w2
b -= lr * g_b
# 每10000轮打印一次损失,避免输出过多
if _ % 10000 == 0:
loss = loss_func(a)
print(f"Epoch {_}, Loss: {loss:.4f}")
print(f"\n最终参数: w1 = {w1:.4f}, w2 = {w2:.4f}, b = {b:.4f}")
# 可视化功能
def visualize():
# 创建画布
plt.figure(figsize=(10, 8))
# 绘制数据点
plt.scatter(class1_points[:, 0], class1_points[:, 1], c='blue', marker='o', label='类别 1')
plt.scatter(class2_points[:, 0], class2_points[:, 1], c='red', marker='x', label='类别 0')
# 绘制决策边界 (w1*x1 + w2*x2 + b = 0)
# 转换为 x2 = (-w1*x1 - b)/w2
x_min, x_max = all_data[:, 0].min() - 0.5, all_data[:, 0].max() + 0.5
x_line = np.linspace(x_min, x_max, 100)
y_line = (-w1 * x_line - b) / w2 if w2 != 0 else np.zeros_like(x_line)
plt.plot(x_line, y_line, 'g-', label='决策边界')
# 添加网格、标签和标题
plt.grid(True, linestyle='--', alpha=0.7)
plt.xlabel('X1', fontsize=12)
plt.ylabel('X2', fontsize=12)
plt.title('逻辑回归分类结果与决策边界', fontsize=14)
plt.legend()
# 添加分类区域的颜色填充
xx1, xx2 = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(all_data[:, 1].min() - 0.5, all_data[:, 1].max() + 0.5, 100))
Z = sigmoid(w1 * xx1 + w2 * xx2 + b)
Z = np.where(Z >= 0.5, 1, 0)
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA'])
plt.contourf(xx1, xx2, Z, cmap=cmap_light, alpha=0.3)
plt.show()
# 调用可视化函数
visualize()
if __name__ == '__main__':
func1()这篇纯手码,看到这里的家人们给个三连,感谢!!!