
写操作
write1:WAL
把操作同步到磁盘中WAL做备份(追加写、性能极高)
write2:Memtable
完成WAL后将(k,v)数据写入内存中的Memtable,Memtable的数据结构一般是跳表或者红黑树
内存内采用这种数据结构一方面支持内存内高速增删改查(时间复杂度O(logM)),另一方面可以保持有序,为写入磁盘中的SSTable打基础
write3:Immutable Memtable
Memtable存储的元素达到一定数量后,就会把它拷贝一份出来成为Immutable Memtable (不可变的Memtable)并且不能对其修改了,新增的数据都写入新的Memtable,这么做的好处是当需要将Memtable转化为Immutable Memtable时无需暂停工作,至于为什么要拷贝一个Immutable Memtable ,这主要是为了后续落盘时做准备
write4:Minor Compaction
内存中的数据不可能无线的扩张下去,需要把内存里面Immutable Memtable 定期dump到到硬盘上的SSTable level 0层中,此步骤也称为Minor Compaction
SSTable的数据结构是LSM-Tree设计的精髓,他一方面可以保持有序,一方面又能利用磁盘追加写的高性能
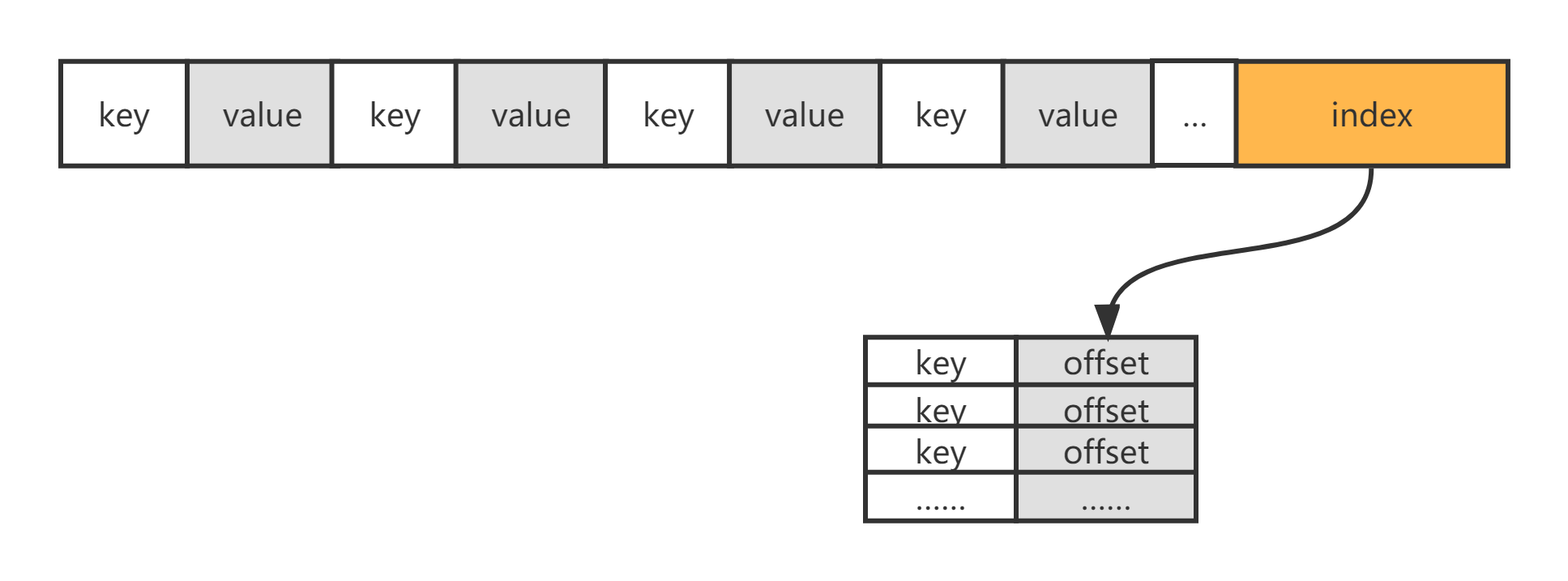
SSTable的数据结构为两部分,前半部分是key与value成对的数据连续存储,这部分数据的key是有序的,后半部分是前半部分的索引,值存储的是key所对应的offset,也是有序的,每次打开这个SSTable需要把索引加载到内存并利用二分搜索可以很快查找出要访问的key的值
dump的过程中每个Immutable Memtable会对应一个SSTable的segment且不会对多个Immutable Memtable进行合并,而是直接将Immutable Memtable中有序的跳表或者红黑树遍历并追加写入到segment,这个过程速度很快。由于不会合并level 0层中的SSTable可能会出现相同的key。
write5、write6:Major Compaction merge
当level 0中的segment越来越多,查询需要遍历的segment也就会越来越多,并且随着时间的推移,重复的key也会越来越多,在后面的步骤就需要对level 0层的segment进行合并merge
合并的过程中是吧多个有序的segment进行归并合并,所以性能不会很差,多个老的segment会合并成一个更长的同样有序的segment并设置到下一层
每一层的segment的数量和大小都会有限制,每当超出限制后,就会做合并操作
虽然定期合并可以有效的清除无效数据,缩短读取路径提升查询效率,提高磁盘利用空间。但Compaction操作是非常消耗CPU和磁盘IO的,尤其是在业务高峰期,如果发生了Major Compaction,则会降低整个系统的吞吐量,这也是一些NoSQL数据库,比如Hbase里面常常会禁用Major Compaction,并在凌晨业务低峰期进行合并的原因。
修改流程
write1:WAL
write2:找到key直接修改或新增key
write3:Immutable Memtable
write4:Minor Compaction
write5、write6...:较新的key(有序可以识别)会替代较老的key
删除流程
write1:WAL
write2:找到key设置状态为tombstone或新增key设置状态为tombstone
write3:Immutable Memtable
write4:Minor Compaction
write5、write6...:因为不确定下层是否有被删除的key,到最后一层merge时才真正删除
读操作
一、按照Memtable(内存)、Immutable Memtable(内存)、level 0 segments(磁盘)、level 1 segments(磁盘)、level 1 segments(磁盘)的顺序查询
二、每层先查新生成的segment
三、每个segment从后向前查
为什么LSM不直接顺序写入磁盘,而是需要在内存中缓冲一下?
单条写的性能没有批量写快,很多中间件比如elasticsearch、kafka、mysql都有类似的内存缓冲设计
在磁盘缓冲的另一个好处是,针对新增的数据,可以直接查询返回,能够避免一定的IO操作
LSM-Tree和B+Tree的比较
LSM-Tree的优点是支持高吞吐的写O1,这个特点在分布式系统上更为看重
针对读取普通的LSM-Tree结构,读取是On的复杂度
在使用索引或者缓存优化后的也可以达到O(logN)的复杂度。
适用于写多读少
B+tree的优点是支持高效的读(稳定的O(logN))
但是在大规模的写请求下(O(LogN)),效率会变得比较低,因为随着insert的操作,为了维护B+树结构,节点会不断的分裂和合并。操作磁盘的随机读写概率会变大,故导致性能降低。
适用于写少读多或写读平衡
log-structured merge-tree (LSM tree) 是一种被精心设计的数据结构,常用于处理大量写入的场景。通过对写入操作进行顺序写入优化实现性能提升。LSM tree 是很多数据库内部的核心数据结构,包括BigTable, Cassandra, Scylla,和 RocksDB。
SSTables
LSM tree 通过一种叫做 SSTable (Sorted Strings Table) 的格式,持久化到硬盘上。正如其名,SSTable 是一种用来存储有序的键值对的格式,其中键的组织是有序存储的。一个SSTable 会包括多个有序的子文件,被称为 segment 。 这些 segments 一旦被写入硬盘,就不可以再修改了。一个简单的SSTable 例子如下图所示:
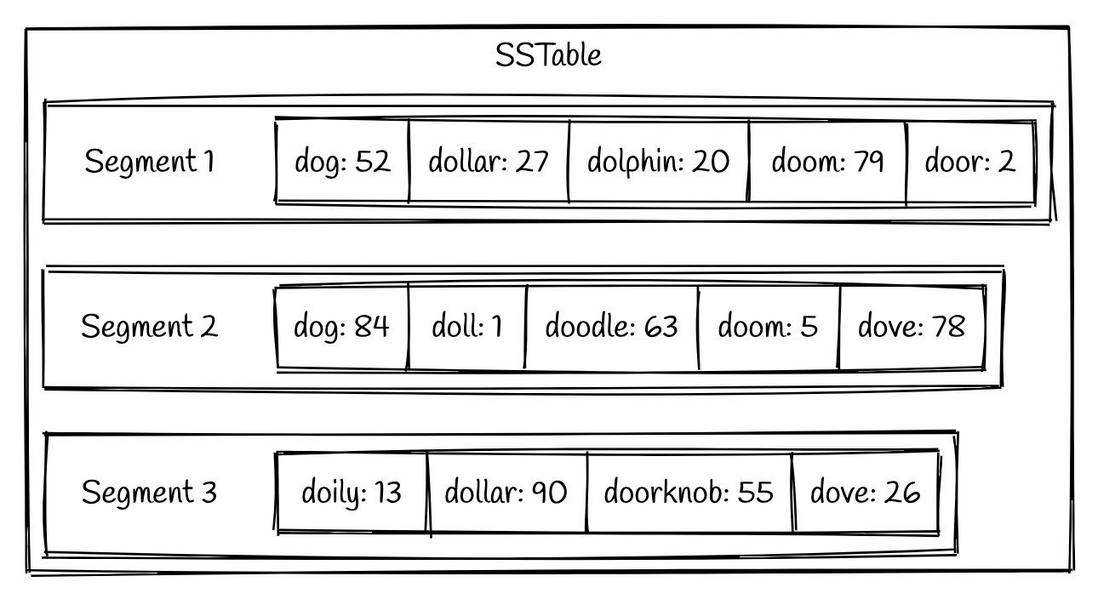
我们可以看到,在每个 segment 中的键值对都是按照键的顺序有序组织的。
写入数据
由于 LSM tree 只会进行顺序写入,所以自然而然地就会引出这样一个问题,写入的数据可能是任意顺序的,我们又如何保证数据能够保持 SSTable 要求的有序组织呢?
这就需要引入新的常驻内存 (in-memory) 数据结构: memtable_了, _memtable 的底层数据结构则有点像红黑树,当由新的写入操作则将数据插入到红黑树中。
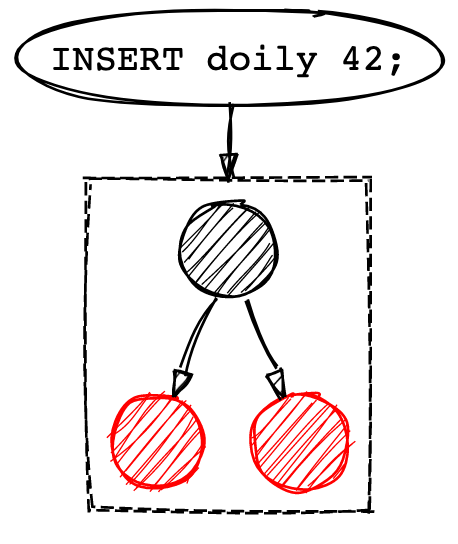
写入操作会先把数据存储到红黑树中,直至红黑树的大小达到了预先定义的大小。一旦红黑树的大小达到阈值,就会把数据整个刷到磁盘中,这个过程就可以把数据保证有序写入了。经过一层数据结构的承接,就可以保证单向顺序写入的同时,也能保证数据的有序了。
读取数据
那么我们是如何从SSTable中查找数据的呢?一种naive的方法就是遍历所有的 segments,寻找我们需要的key。从最新的 segment 到最老的 segment 一一遍历,知道找到目标key为止。显然,这种方式在寻找刚刚写入的数据是比较快的,但是文件一多就不太行了。因此也有针对这个问题的优化,稀疏索引 就是一种在内存中对数据检索进行优化的技术。
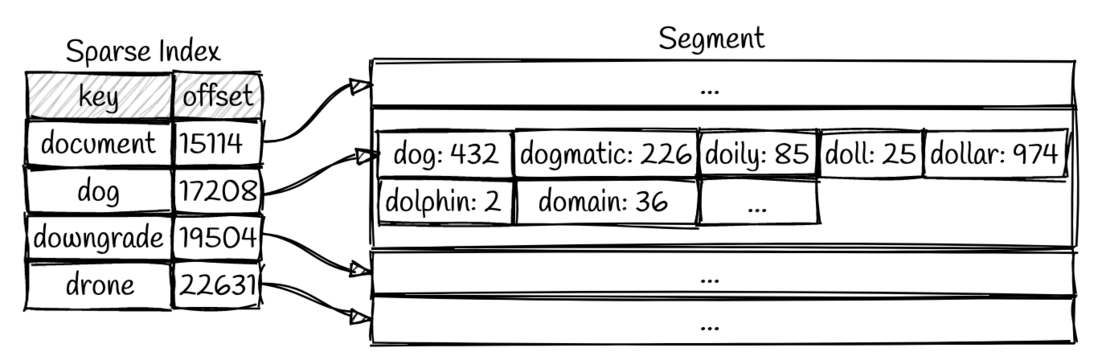
我们可以通过这个索引快速找到所需键的前面和后面的偏移量(就是最近的相邻值),这样我们就只需要扫描很小一部分的 segments 文件就可以了。以如图所示的场景举例,当我们需要搜索 dollar 这个值,我们可以通过二分查找搜索稀疏索引,可以知道 dollar 处于 dog 和 downgrade之间。因此我们只需要搜索 17208 和 19504 之间的 segment 来得到我们所需的值,如果搜索不到则可返回未命中。
译者注:稀疏索引和跳表都是为了解决快速索引的问题,根据不同设计具体选择。
上面优化在查找存在的数据其实已经不错了,但是在搜索不存在的key值的时候还是要遍历所有的 segment 才可以确定。为了解决这个问题,就需要引入 布隆过滤器 。布隆过滤器是一种以空间换时间的数据结构,能够帮助我们快速确定某个值是否不存在(如果布隆过滤器认为该值存在,也可能是实际不存在的)。我们可以在写入数据的时候同时更新布隆过滤器,来加速不存在数据的检索。
数据合并
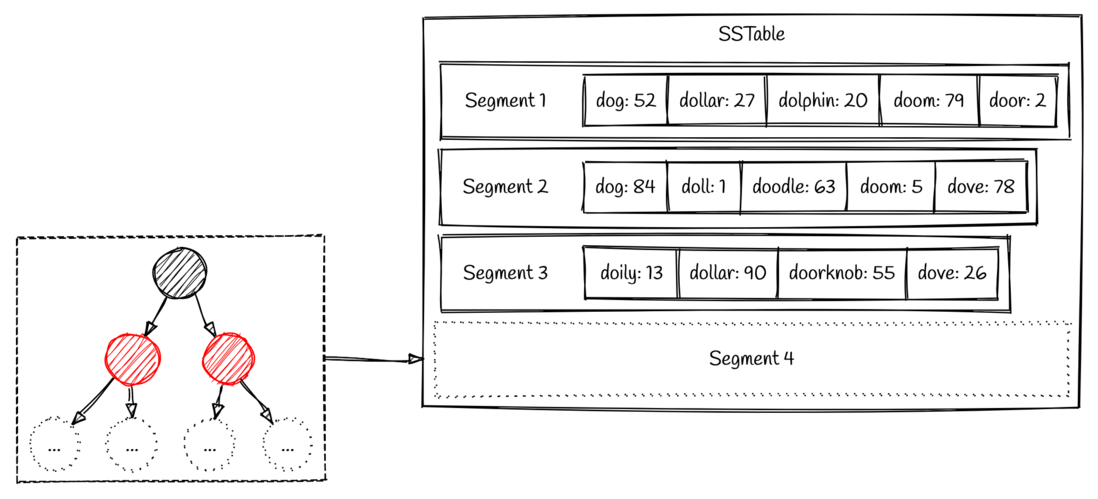
随着时间的推移,整个存储系统将会存储非常多的segment文件,所以这些文件需要进行一定的整理和合并,避免文件太多无法访问。这个文件整理的过程被称为"数据合并" (compaction)。数据合并是一个后台线程,将会持续地将老的segment 合并到一起变成新的 segment。
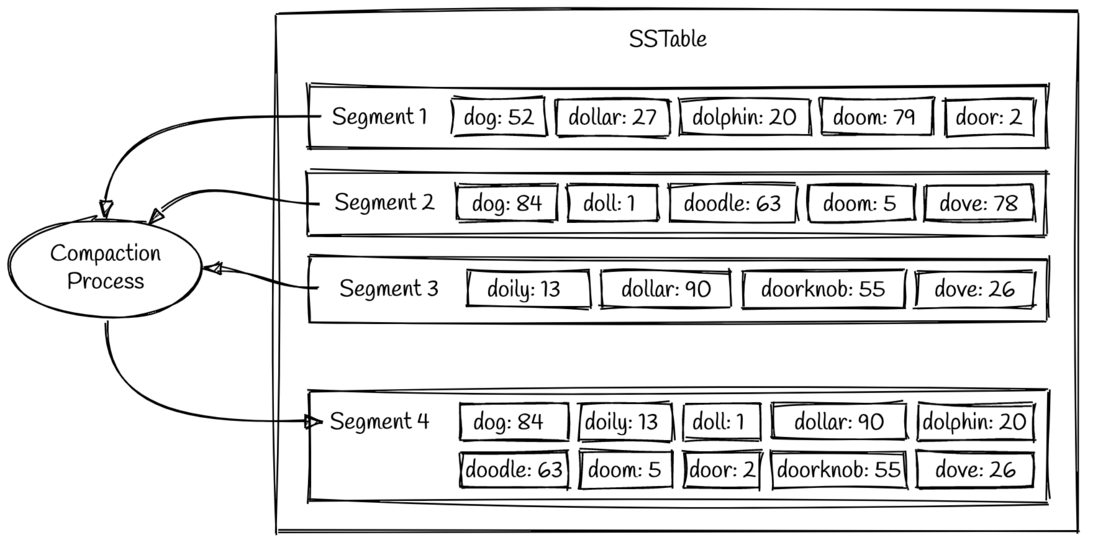
如图所示,我们可以看到 segment 1 和 segment 2 都有 key 为 dog 的两个值。合并后的新 segment 将会保留更新的值,因此会保留原有 segment 2 里面的值 84,即segment 4 中的值是 dog => 84。一旦合并过程已经完成新的 segment 写入,那么原有的老 segment 文件将会被删除。
删除数据
我们已经解释了读取数据和写入数据的过程,那么删除数据又是如何处理的呢?我们已经知道 SSTable 是不可变的,所以里面的数据当然也不能够删除。其实删除操作其实和写入数据的操作是一样的,当需要删除数据的时候,我们把一个特定的标记(我们称之为 墓碑(tombstone) )写入到这个key对应的位置,以标记为删除。
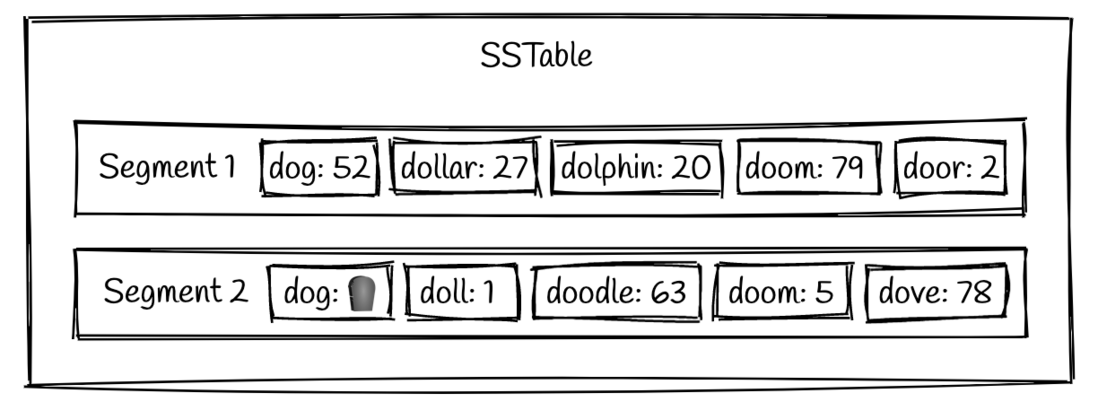
上图演示了原来 key 为 dog 的值为 52,而删除之后就会变成一个墓碑的标记。当我们搜索键 dog的时候,将会返回数据无法查询,这就意味着删除操作其实也是占用磁盘空间的,最后墓碑的值将会被压缩,最后将会从磁盘删除。
总结
我们已经基本描述了 LSM tree 引擎是如何工作的:
- 写入操作是先写入内存的(被成为 memtable)。所有的用于加速查询的数据结构(布隆过滤器和稀疏索引)都会被同时更新;
- 当内存中的 memtable 太大了,将会被刷到磁盘中,注意是有序的;
- 当查询时我们先回查询布隆过滤器,如果布隆过滤器返回说键不存在,则实际不存在,如果布隆过滤器说存在,进一步遍历 segment 文件;
- 对于遍历 segment 文件的过程,我们将会先通过稀疏索引找到最小的文件范围,并开始由新到老开始遍历,找到一个key则直接返回。
参考
https://www.cnblogs.com/zxporz/p/16021373.html
后端 - 理解 LSM Tree : 是什么让数据库这么能写? - codestack - SegmentFault 思否