在学习一个科目前,了解其整体框架非常重要,有助于你快速把握接下来要学的知识点之间的关系,并帮助从已知推导到未知;当完成整体把握后,再自上而下的贯穿每个小知识点,会更让人感觉有道理和容易,知道这个点是干什么用的。
一、数据结构总体框架
一个数据结构主要由以下三要素构成:
- 逻辑结构
- 物理结构(又称存储结构)
- 运算操作
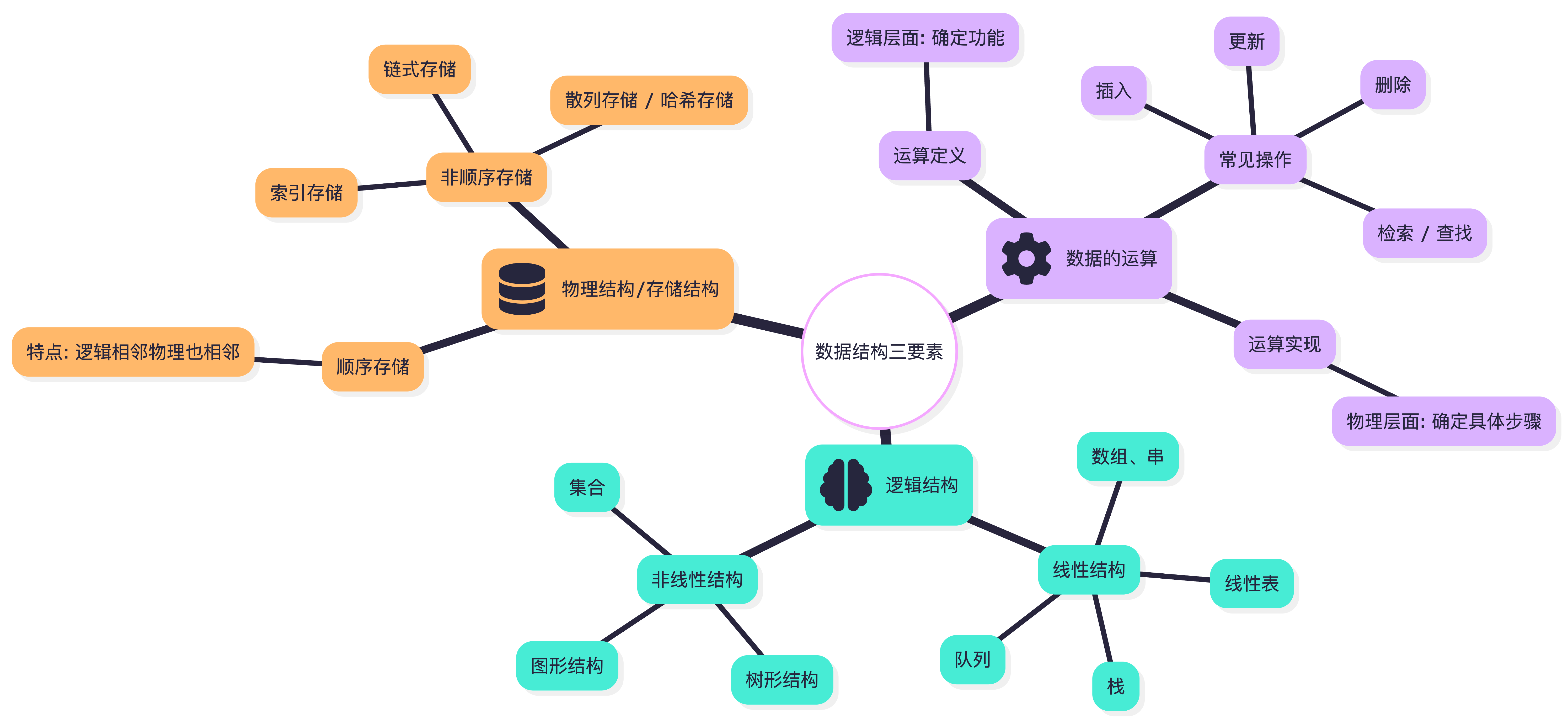
二、逻辑结构
逻辑结构,表示了数据元素之间的逻辑关系,亦即从逻辑关系上描述数据。
逻辑结构本身与物理存储结构无关,大体上可以分为:
- 集合
- 线性表
- 树
- 图
其中,集合在 408 考试中几乎没有出现过,故暂不赘述。线性表属于线性结构,树和图属于非线性结构
以线性表为例:线性表主要可以分为一般线性表、队列和栈,接下来拿队列举例子,来描述一个逻辑结构:
队列
队列作为一个逻辑结构,有如下两种特性:
- 入队:只能从队尾入队,即将插入数据时只能在 tail 的位置插入
- 出队:只能从队首入队,即将删除数据时只能在 head 的位置删除
这一逻辑结构对应生活中的排队打饭,可以描述为如下情形:
- 当有人要加入打饭队列时,应该排到队尾,而不应该插队
- 当打饭窗口空出来时,应该由队首的人先去打饭,而不应该由除了队首以外的人去打饭。
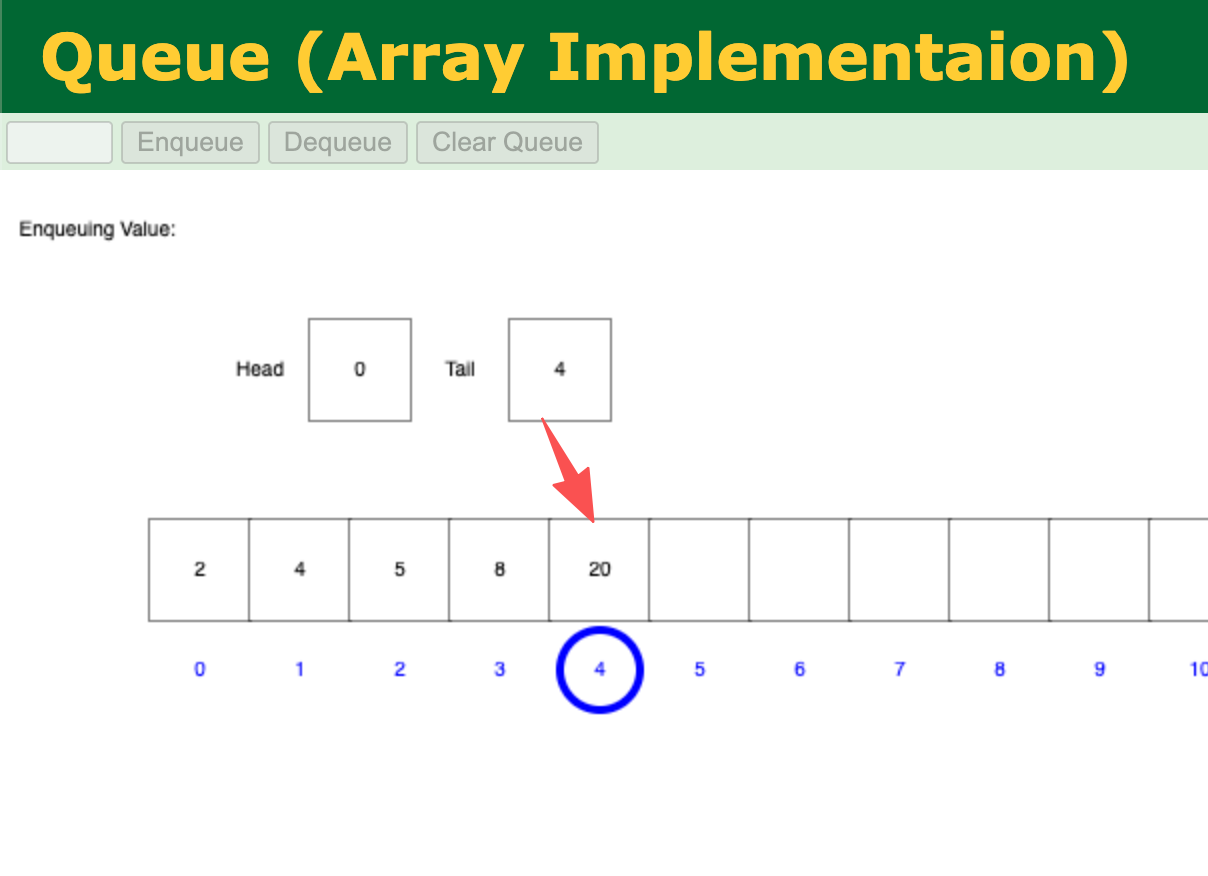
上图描述了 20 这个元素由队尾入队
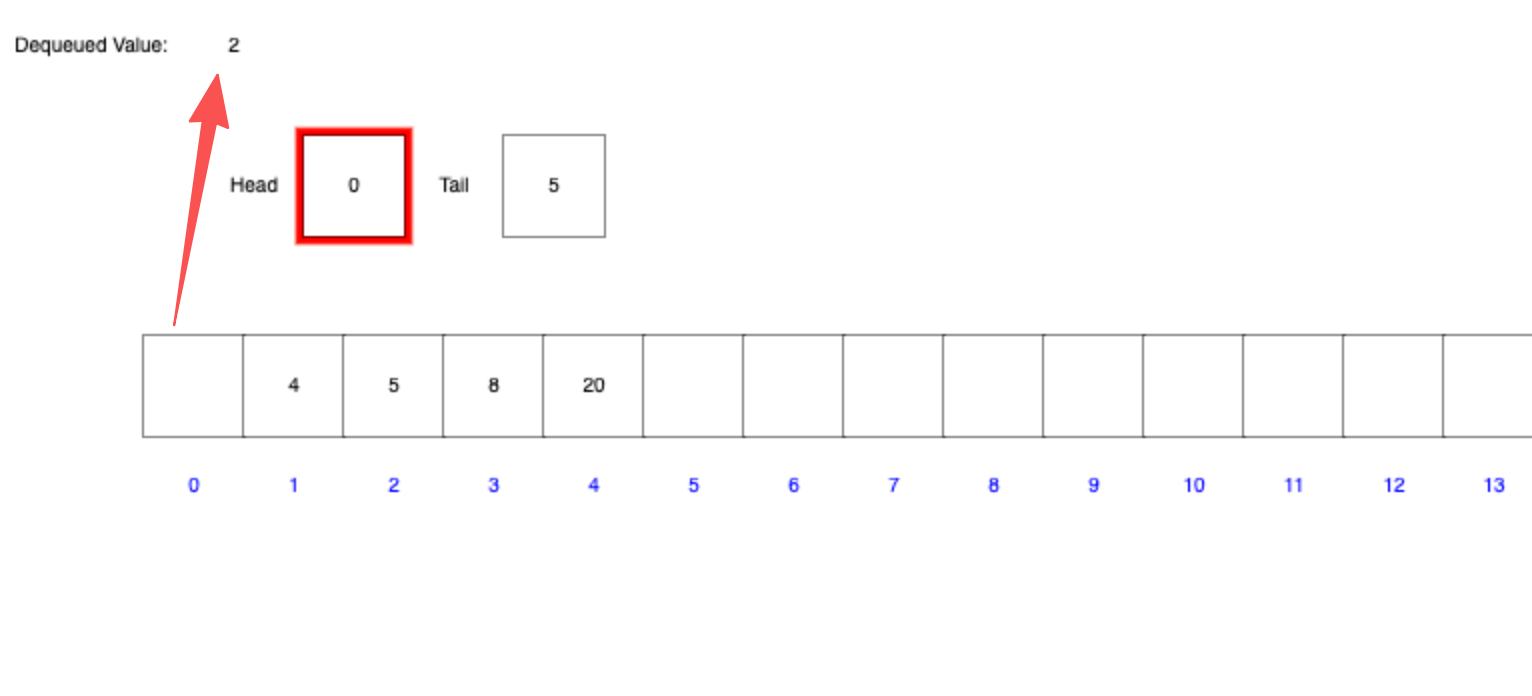
上图描述了 2 从队首出队
总结:综上所述,逻辑结构是从现实世界抽象的数学模型,与物理结构,即该逻辑模型是怎么在计算机内存当中存储的,是独立的;确定了逻辑结构后,才应该确定物理结构
三、物理结构
计算机并不能直接处理一个逻辑模型,而应该通过将逻辑结构转化为计算机中存储结构的方式,实现数据结构在计算机中的存储。
常见的物理结构有:
- 顺序表
- 链式表
- 散列表
- 索引表
其中,只有 1 是顺序的存储方式,其余都是非顺序的。
不同的物理结构必然有不同操作方式(运算)的实现
举个简单的例子,对于同样逻辑结构为线性表,但物理结构一个是顺序表,一个是链表的两个数据结构,他们对于查询的时间复杂度不一样。
当我要查找第n个元素时,对于顺序表,只需要访问 arr[n-1]这个元素即可,时间复杂度为O(1);而对于链表,需要访问链表 n 次,时间复杂度为 O(n)。
四、运算
王道对数据结构运算的解释:施加在数据上的运算包括运算的定义和实现。运算的定义是针对逻辑结构的,运算的实现是针对存储结构的
运算包括但不限于:查找、插入、删除、修改、相加
在我看来,经典的合并二有序链表问题也是一个运算,即把两个以链式存储的线性表给合并的操作:为了实现该算法,应该首先根据线性表的特性,给出合并运算的定义;再根据链式存储的物理结构,给出合并的具体实现:例如为了实现一遍扫描的算法和利用链表特性,设计边遍历边比较边插入的算法等等。
如有错误,敬请指出!