二分算法模版——基础二分查找，左边界查找与右边界查找（Leetcode的二分查找、在排序数组中查找元素的第一个位置和最后一个位置）

首先，定义区间两端变量left和right，一般来说，left = 0，right = len - 1，其中len表示数组元素个数。
其次，计算中间元素下标mid ，取出中间元素n[mid]。
接着，比较n[mid] 和target的 大小。根据升序特性可知，如果k < mid ，那么n[k] < n[mid] ；反之，n[k] < n[mid]。
如果n[mid] > target ，设目标元素下标为x ，可得x 属于**[left, mid - 1]**区间，right = mid - 1。
如果n[mid] < target ，设目标元素下标为x ，可得x 属于**[mid + 1, right]**区间，left= mid + 1。
如果**n[mid] == target，**可以直接返回下标mid。
上面是一轮比较，可以加上while循环，循环条件是left <= right。

二分算法每次比较完后，可以淘汰数组中一半的元素。假设元素个数为N，且最多使用x次得出结果，则有公式，可得，时间复杂度为O(log n) 。

（3）注意事项

中间值

如果使用该式子mid = (left + right) / 2 计算中间值，可能会遇到数据量太大，数值溢出的情况，这个时候可以使用mid = left + (right - left) / 2，来计算中间值。

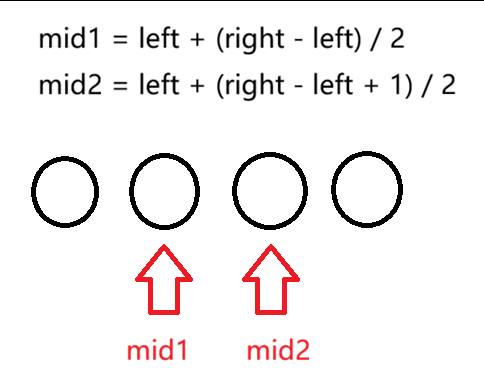
有时，可能还会遇到mid = (left + right + 1) / 2 和 mid = left + (right - left + 1) / 2这两个式子，在这个题目中，用那个都行。

mid = left + (right - left) / 2 和 mid = left + (right - left + 1) / 2唯一的区别就是，当数组个数为偶数时，使用第一个式子计算出中间值，在左端；使用第二个式子计算出中间值，在右端。

循环条件

题目给出的数组的元素是按照严格升序排列，无重复元素，并且每次更新left或者right变量，都会抛弃mid下标元素，所以循环条件可以使left <= right。

当left == right时，表示区间已经缩小到一个下标，如果该元素值不等于target，则数组中没有等于target的元素。

（4）题解代码

题目代码如下：

cpp 复制代码

    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if (target > nums[mid])
                left = mid + 1;
            else if (target < nums[mid])
                right = mid - 1;
            else
                return mid;
        }

        return -1;
    }

这种二分算法解题步骤是朴素二分算法，利用数组有序的特性。可数组不是必须满足有序特性才可以使用二分算法，只需要数组拥有二段性，即可使用二分算法。

2. 在排序数组中查找元素的第一个位置和最后一个位置

（1）题目及示例

题目链接： https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为**O(log n)**的算法解决此问题。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]

示例 3：

输入： nums = [], target = 0
输出：[-1,-1]

提示：

0 <= nums.length <= 105 -109 <= nums[i] <= 109

nums 是一个非递减数组 -109 <= target <= 109

（2）查找左端点

这道题目跟第一题类似，如果直接遍历数组，那么时间复杂度为O(n)。

题目数组按照非递减顺序排列，其中可以出现重复元素。直接使用第一题二分算法解题思路，得到的target值下标不一定是，第一个位置和最后一个位置。

此时，我们可以利用二段性。二段性是什么呢？我的理解是，给出一个数组nums，查找target值下标x。该数组拥有一个特性，可以判断下标x是属于**[left, mid]** ，还是**[mid, right]** 。

算法步骤

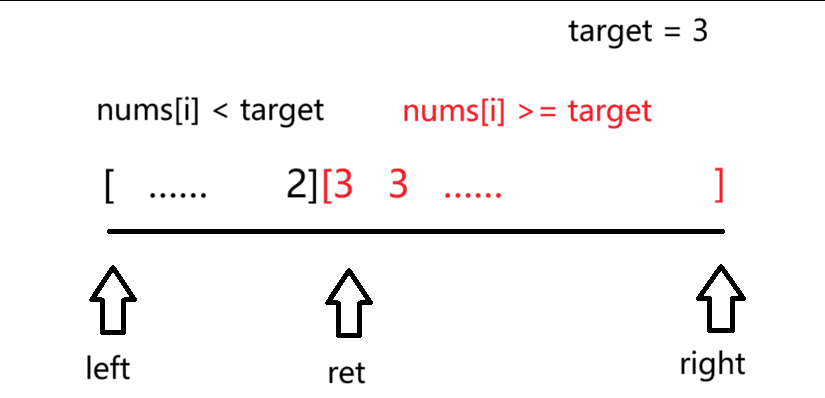
如下图所示，我们将一个数组抽象成一条黑色线段。查找目标值左端点时，我们可以将该数组分割成两个部分**[left, ret - 1** ] 和 [ret, right]。

在**[left, ret - 1** ]区间中，任意下标 i，都满足nums[i] < target。
在**[ret, right** ]区间中，任意下标 i，都满足nums[i] >= target。
假设target = 3，那么数组可能出现下面的排列情况。

查找目标值左端点的二分算法步骤与第一题类似，如下：

首先，定义区间两端变量left和right，一般来说，left = 0，right = len - 1，其中len表示数组元素个数。
其次，计算中间元素下标mid ，取出中间元素n[mid]。
接着，比较n[mid] 和target的大小。
如果n[mid] >= target ，设目标元素下标为x ，因为nums[mid]可能是目标值的第一个位置，所以x 属于**[left, mid]**区间，right = mid。
如果n[mid] < target ，设目标元素下标为x ，可得x 属于**[mid + 1, right]**区间，left= mid + 1。
上面是一轮比较，可以加上while循环，循环条件是left < right。

循环条件

查找目标左端点时，循环条件为left < right，而不是left <= right。这是为什么呢？

我们假设该数组目标左端点存在，根据二分算法步骤，可知right变量不管如何移动，最终落点都会在红色闭区间中。那么right最后会等于ret，而left变量想要跳出黑色区间，最后也会指向ret。

我们可以得出结论，当left = right时，就是最终结果，无需判断。

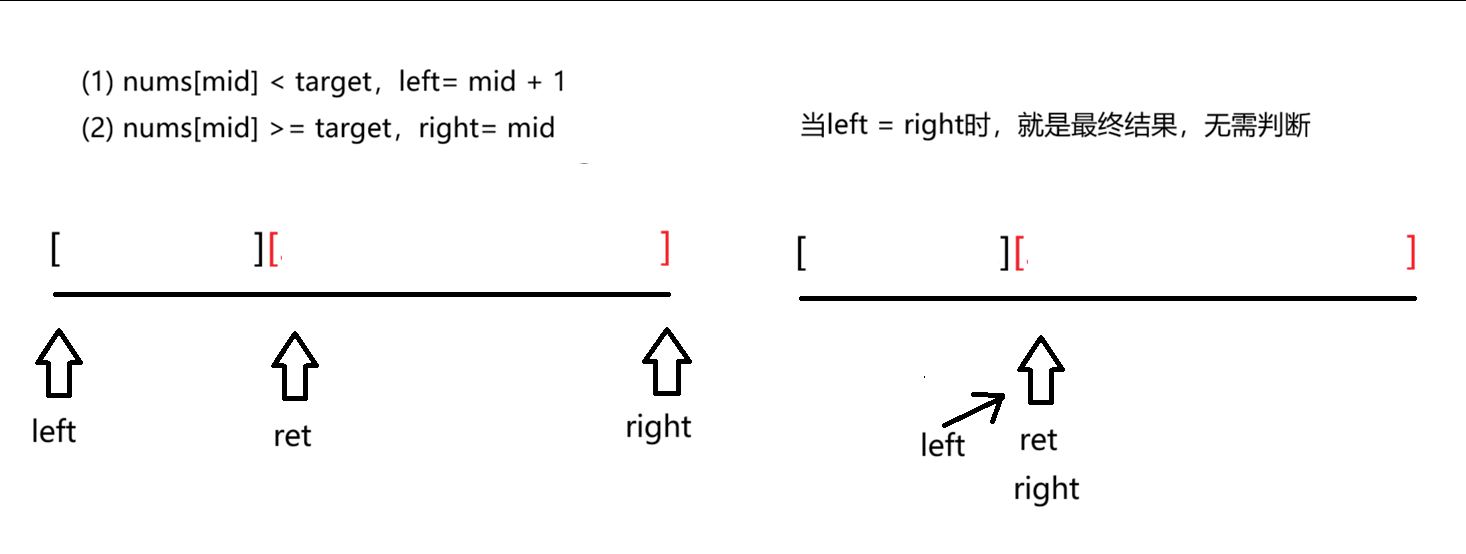
当数组的所有元素都大于target值，right指向的元素会不断左移，直到指向第一个元素。当left = right时，就是最终结果，只需要判断nums[left]是否等于target就行。

如果循环判断条件是left <= right ，当left = right 时，计算出的mid = left = right。
根据算法步骤right 还是赋值成mid。此时，还是满足循环条件，会陷入死循环！

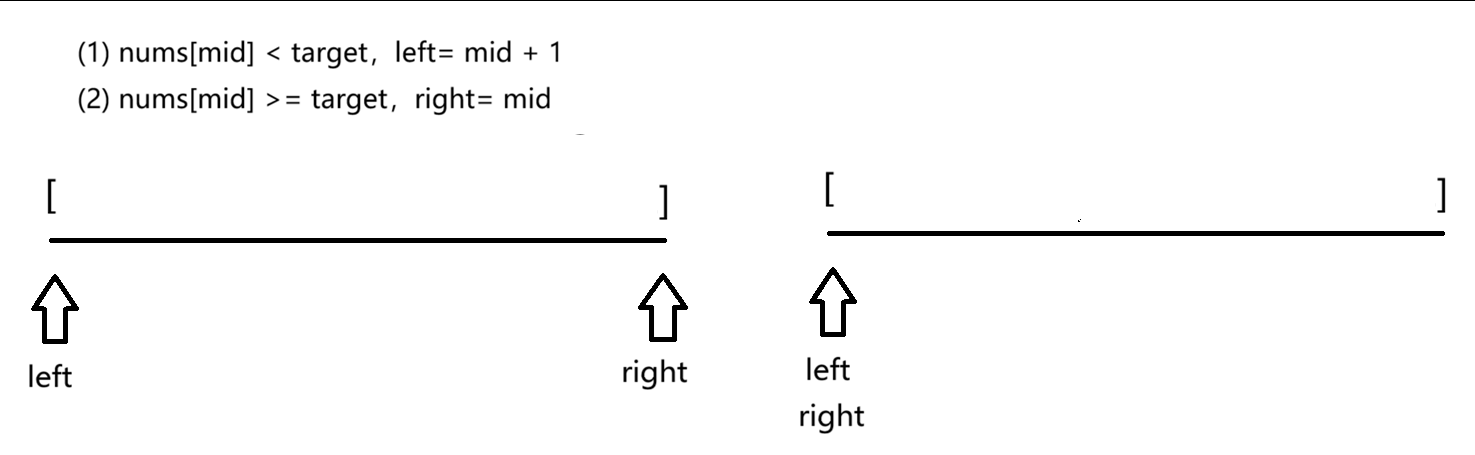
当数组的所有元素都大于target 值，left指向的元素会不断右移，直到指向最后一个元素。

当当left = right时，就是最终结果，只需要判断nums[left]是否等于target就行。

中间值

这次的中间值计算只能采用mid = left + (right - left) / 2 ， 不能使用mid = left + (right - left + 1) / 2。我们可以通过极端情况进行分析：

我们假设数组只有两个元素，两种不同计算mid值方法，得出的mid值不同，一个在左端点，一个在右端点。

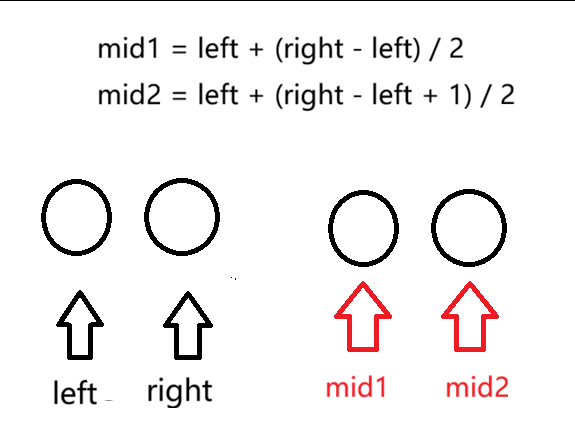
如果使用mid = left + (right - left) / 2，不会出现死循环的情况。

当n[mid] < target 时，left = mid1 + 1 = right，不满足循环条件，跳出循环。
当n[mid] >= target 时，right = mid1 = left，也不满足循环条件，跳出循环。

如果使用mid = left + (right - left + 1) / 2，会出现死循环的情况。

当n[mid] < target 时，left = mid1 + 1 > right，不满足循环条件，跳出循环。
当n[mid] >= target 时，right = mid1 = right ，满足循环条件left < right ，下一轮计算出的mid还是等于right ，因此会陷入死循环！

(3) 查找右端点

算法步骤

如下图所示，我们将一个数组抽象成一条黑色线段。查找目标值右端点时，我们可以将该数组分割成两个部分**[left, ret** ] 和 [ret + 1, right]。

在**[left, ret** ]区间中，任意下标 i，都满足nums[i] <= target。
在**[ret, right + 1** ]区间中，任意下标 i，都满足nums[i] > target。
假设target = 3，那么数组可能出现下面的排列情况。

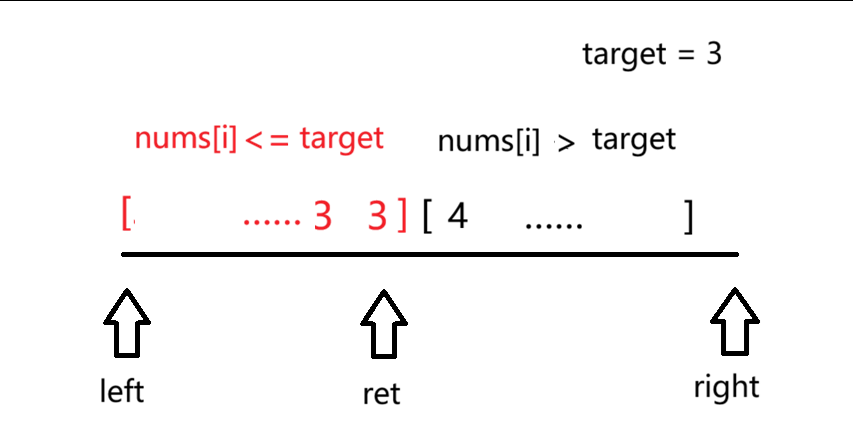
查找目标值左端点的二分算法步骤与第一题类似，如下：

首先，定义区间两端变量left和right，一般来说，left = 0，right = len - 1，其中len表示数组元素个数。
其次，计算中间元素下标mid ，取出中间元素n[mid]。
接着，比较n[mid] 和target的大小。
如果n[mid] > target ，设目标元素下标为x ，因为nums[mid]可能是目标值的第一个位置，所以x 属于**[left, mid]**区间，right = mid - 1。
如果n[mid] <= target ，设目标元素下标为x ，可得x 属于**[mid + 1, right]**区间，left= mid。
上面是一轮比较，可以加上while循环，循环条件是left < right。

循环条件

查找目标值右端点的循环条件也是left < right，大家可以参照上面的内容自行分析。

中间值

中间值计算只能采用**mid = left + (right - left + 1) / 2 ，**大家可以参照上面的内容自行分析。

（4）题解代码

cpp 复制代码

    vector<int> searchRange(vector<int>& nums, int target) 
    {
        int size = nums.size();
        if (size == 0)//空数组直接返回一对-1
            return {-1,-1};

        vector<int> ret;
        int left = 0, right = size - 1;
        while(left < right)//不能加上等于号，会出现死循环
        {
            //偶数情况下，求出来的点偏左边
            //如果加1，会死循环
            int mid = left + (right - left) / 2;

            if (nums[mid] < target)//根据两段性，
                left = mid + 1;
            else
                right = mid;
        }
        if (nums[left] != target)
            return {-1, -1};
        ret.push_back(left);

        left = 0, right = size - 1;
        while(left < right)
        {
            //偶数情况下，求出来的点偏右边            
            int mid = left + (right - left + 1) / 2;

            if (nums[mid] > target)
                right = mid - 1;
            else
                left = mid;
        }
        ret.push_back(left);

        return ret;
    }

总结

二分查找算法的三种核心解题模板可以帮助解决循环条件和中间值计算模糊的问题。不同题目具有各自的二段性特征，需要根据实际情况灵活调整算法实现细节。

创作充满挑战，但若我的文章能为你带来一丝启发或帮助，那便是我最大的荣幸。如果你喜欢这篇文章，请不吝点赞、评论和分享，你的支持是我继续创作的最大动力！