



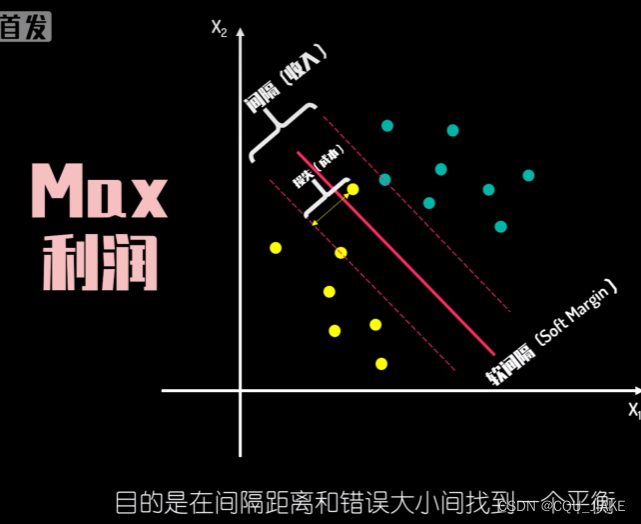
软间隔、硬件隔

升维,核技巧



目标函数




拉格朗日

如果在约束边界线上,就是紧约束,朗姆达就不等于0,表示起到约束效果,而且约束条件=0
不在的话,就不是,朗姆达就等于0,相当于没起到约束效果



KKT条件,对偶问题
最优解仅与支持向量有关,即只与约束边界上的点有关

首先是要保证约束条件不等式是大于等于0的,然后给约束条件乘个朗姆达,再给它减到原函数里,如果满足约束条件,那么不等式大于0,对于朗姆达,如果是负的话,在不满足约束条件时,为负,那么乘负,再减,还是负,就导致最后结果小于0,就相当于鼓励违反约束条件,所以朗姆达一定是正的或者为0
 、
、
KKT要改为的形式如上所述


只有相切的地方,梯度方向相反,相加后,才能使新函数的梯度为0,实际就是把新函数拆分为目标函数和约束函数,然后新函数的梯度就是这俩函数的梯度向量和
即目标函数的梯度向量加上约束函数的梯度向量等于0,即方向相反,大小相等,方向是靠约束取点来实现,大小相等是靠拉格朗日乘子朗姆达来实现


如果gX等于0的话,就说明约束条件起到了作用,那么就需要调整朗姆达来使之最后的结果加和为目标函数的方向相反,大小相等的向量
如果不等于0的话,说明没起作用,那么最后的向量上就不应该有它的贡献,所以就要让朗姆达为0,表示不起作用

如果在可行域的话,那么约束条件都满足;不在可行域的话,一定都不满足约束条件


满足约束条件时,小于等于0,要让它最大,必然为0,那最后就只剩下了原函数


对x求梯度为0,实际就是在x下最小值



就是说同一个函数里最小值里的最大值一定小于等于其最大值里的最小值




作业题


RBF
clear
x=[0 0;0 1; 1 0;1 1];
y=[0;1;1;0];
hideNum=10; %隐层神经元数目,要求必须大于输入层个数
rho=rand(4,hideNum); %径向基函数的值
py=rand(4,1); %输出值
w=rand(1,hideNum); %隐层第i个神经元与输出神经元的权值
beta=rand(1,hideNum); %样本与第i个神经元的中心的距离的缩放系数
eta=0.5; %学习率
c=rand(hideNum,2); %隐层第i个神经元的中心
kn=0; %累计迭代的次数
sn=0; %同样的累积误差值累积次数
previous_E=0; %前一次迭代的累积误差
while(1)
kn=kn+1;
E=0;
%计算每个样本的径向基函数值
for i=1:4
for j=1:hideNum
p(i,j)=exp(-beta(j)*(x(i,:)-c(j,:))*(x(i,:)-c(j,:))');
end
py(i)=w*p(i,:)';
end
%计算累积误差
for i=1:4
E=E+((py(i)-y(i))^2); %计算均方误差
end
E=E/2; %累积误差
%更新w、beta
delta_w=zeros(1,hideNum);
delta_beta=zeros(1,hideNum);
for i=1:4
for j=1:hideNum
delta_w(j)=delta_w(j)+(py(i)-y(i))*p(i,j);
delta_beta(j)= delta_beta(j)-(py(i)-y(i))*w(j)*(x(i,:)-c(j,:))*(x(i,:)-c(j,:))'*p(i,j);
end
end
%更新w、beta
w=w-eta*delta_w/4;
beta=beta-eta*delta_beta/4;
%迭代终止的条件
if(abs(previous_E-E)<0.0001)
sn=sn+1;
if(sn==50)
break;
end
else
previous_E=E;
sn=0;
end
end



6.5
若将隐层神经元数设置为训练样本数,且每个训练样本对应一个神经元中心,则以高斯径向基函数为激活函数的RBF网络恰与高斯核SVM的预测函数相同。
6.6
SVM的决策只基于决策边界的支持向量,如果支持向量含有噪音,就会对决策造成影响,因此SVM对噪音敏感。
