Java版-图论-最小生成树-Kruskal算法

实现描述

为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 n-1 条边，即形成了一棵树。

实现代码

首选我们对所有的边，按照权重排序；
之后，从小到大选择边，如果当前的边已经连通过了，则放弃此边，查看下一条边；若没有连通过，通过并查集进行连通；
直至所有点都访问过，此时，完成。

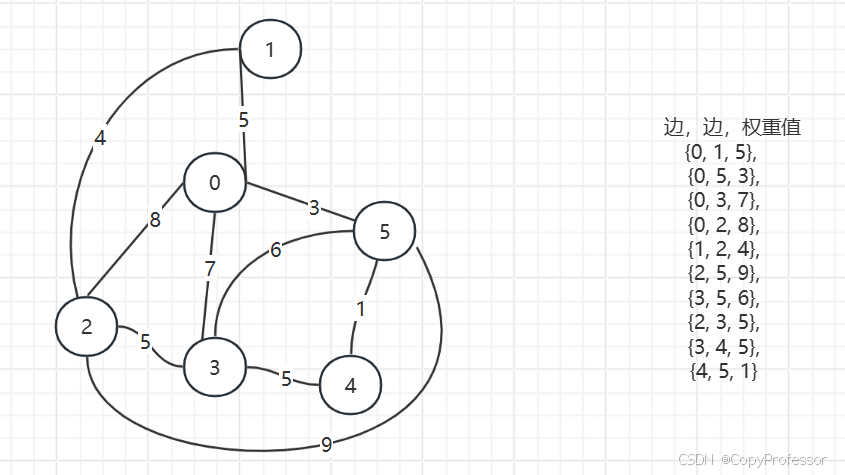
如上图，节点0~5，边关系如上；

先对边权重进行从小到大排序，得到：

java 复制代码

[{
	"u":4,
	"v":5,
	"weight":1
},{
	"u":0,
	"v":5,
	"weight":3
},{
	"u":1,
	"v":2,
	"weight":4
},{
	"u":0,
	"v":1,
	"weight":5
},{
	"u":2,
	"v":3,
	"weight":5
},{
	"u":3,
	"v":4,
	"weight":5
},{
	"u":3,
	"v":5,
	"weight":6
},{
	"u":0,
	"v":3,
	"weight":7
},{
	"u":0,
	"v":2,
	"weight":8
},{
	"u":2,
	"v":5,
	"weight":9
}]

然后依次选择排序后的边：

下面代码对应上图数据及其过程：

java 复制代码

import com.alibaba.fastjson.JSONObject;
import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;
import org.jetbrains.annotations.NotNull;

import java.util.*;

public class kruskal {

    /**
     * 边定义
     */
    @Data
    @AllArgsConstructor
    @NoArgsConstructor
    static class Edge implements Comparable<Edge> {
        int u, v;
        int weight;

        @Override
        public int compareTo(@NotNull Edge o) {
            return weight - o.weight;
        }
    }


    static List<Edge> getKruskalEdges(int nodeNum, int[][] grid) {
        List<Edge> result = new LinkedList<>();
        List<Edge> edges = new LinkedList<>();
        for (int i = 0; i < grid.length; i++) {
            int u = grid[i][0];
            int v = grid[i][1];
            int weight = grid[i][2];
            edges.add(new Edge(u, v, weight));
        }
        Collections.sort(edges);
        UnionFindTemplate uf = new UnionFindTemplate(nodeNum);
        Set<Integer> visited = new HashSet<>();
        for (Edge edge : edges) {
            if (uf.connected(edge.u, edge.v)) {
                continue;
            }
            uf.union(edge.u, edge.v);
            visited.add(edge.u);
            visited.add(edge.v);
            result.add(edge);
            if (visited.size() == nodeNum) {
                break;
            }
        }
        return result;
    }



    public static void main(String[] args) {
        int nodeNum = 6;
        int[][] grid = {
                {0, 1, 5},
                {0, 5, 3},
                {0, 3, 7},
                {0, 2, 8},
                {1, 2, 4},
                {2, 5, 9},
                {3, 5, 6},
                {2, 3, 5},
                {3, 4, 5},
                {4, 5, 1}
        };
        System.out.println(JSONObject.toJSONString(getKruskalEdges(nodeNum, grid)));
    }
}

其中，并查集模版的实现如下：

java 复制代码

public class UnionFindTemplate {
    int[] parent;
    int[] size;
    int n;
    public int setCount;//连通分量个数

    public UnionFindTemplate(int n) {
        this.n = n;
        this.parent = new int[n];
        this.size = new int[n];
        setCount = n;
        Arrays.fill(this.size, 1);
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    public int findParent(int x) {
        if (parent[x] == x) {
            return x;
        } else {
            parent[x] = findParent(parent[x]);
            return parent[x];
        }
    }

    public void union(int x, int y) {
        x = findParent(x);
        y = findParent(y);
        if (x == y) {
            return;
        }
        if (size[x] < size[y]) {
            int temp = x;
            x = y;
            y = temp;
        }
        //y合并到x
        parent[y] = x;
        size[x] += size[y];
        setCount--;
    }

    public boolean connected(int x, int y) {
        x = findParent(x);
        y = findParent(y);
        return x == y;
    }

}