从零开始的C++之旅——红黑树封装map_set

1.map_set的封装

1.1 总体思想

map和set中储存的数据类型并不相同，然而库中的map和set底层是用了同一颗红黑树来实现的，这其中便体现了泛型编程的思想。

通过模板传入不同类型的参数，从而实例化出对应类型的红黑树节点来进行套用。

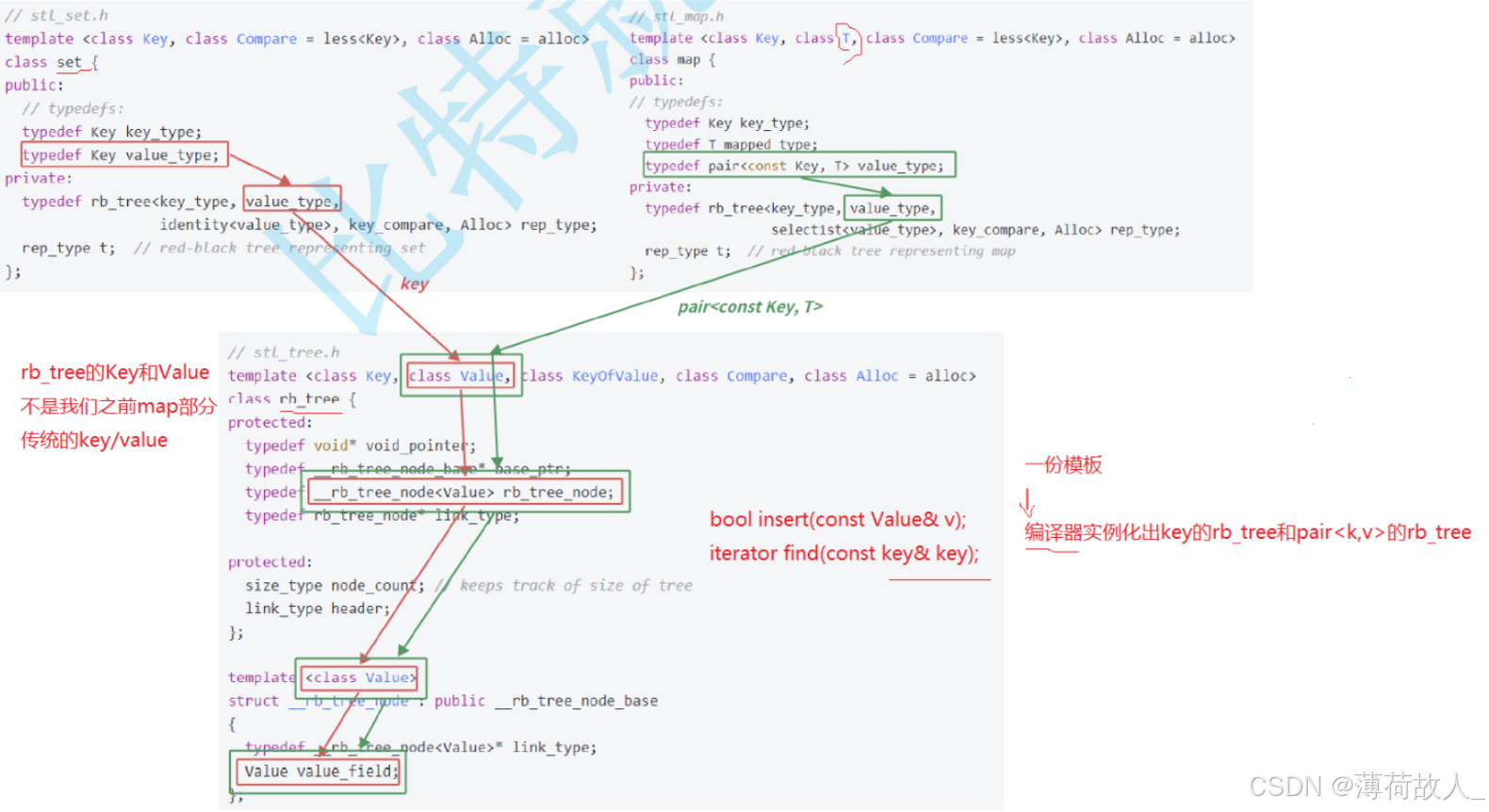
用模板来初始化节点，通过模板参数来控制实例化出不同类型的节点，便实现泛型编程，不过此处泛型编程也有一些需要注意的点，我们再后续会提到。

1.2 复用红黑树的框架

我们再套用红黑树框架时，由于泛型编程，需要对其进行改动。

1.2.1 红黑树的节点

前面提到我们使用模板来初始化节点，因此节点的类型取决于传入的参数，这里设为 T。其余不变。

template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Color _color;

	RBTreeNode(const T& data)
		:_data(data)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{}

};

1.2.2 红黑树的插入

由于泛型编程的理念，我们的红黑树节点类型为T，所以红黑树的插入也要有所改动，因为对于set来说，我们是直接根据key进行节点比较从而寻找插入位置，而对于map来说其节点类型是pair类型，我们需要对其进行解引用取first成员。

那么我们怎么实现泛用的红黑树插入操作呢，答案是使用仿函数。

我们在红黑树的模板参数多加了一个参数KeyOfT，其目的便是用来取出对应类型中的ket值用于进行比较运算。

对于map，我们在其中实现一个仿函数MapOfT，用于返回其pair类型的first，也就是key值。

对于set，我们在其中实现一个仿函数SetKeyOfT，只需直接返回key值即可，虽然有些多此一举但这样实现了泛型编程，同时性能是也没有很大牺牲。

	bool Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_color = BLACK;

			return true;
		}

		KeyOfT kot;
		Node* parent = _root;
		Node* cur = _root;
		while (cur)
		{
			if (kot(data) < kot(cur->_data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(data) > kot(cur->_data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		//找到节点位置,连接起来
		cur = new Node(data);
		cur->_parent = parent;
		cur->_color = RED;

		//记录插入位置，用于返回值
		//防止cur向上变色丢失插入位置
		Node* newnode = cur;
		if (kot(data) < kot(parent->_data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		
		//父亲节点为红，出现了连续的红色节点，需要进行处理
		//循环处理，直到头节点或父节点为黑
		while (parent && parent->_color == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				//    g
				//  p   u
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_color == RED)//舅舅存在且为红
				{
					parent->_color = uncle->_color = BLACK;
					grandfather->_color = RED;
					
					//继续向上更新
					cur = grandfather;
					parent = grandfather->_parent;
				}
				else//舅舅不存在或舅舅为黑
				{
					//     g
					//   p   u
					//c
					//单旋+变色
					if (parent->_left == cur)
					{
						RotateR(grandfather);
						parent->_color = BLACK;
						grandfather->_color = RED;
					}
					//     g
					//   p   u
					//     c
					//双旋+变色
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_color = BLACK;
						grandfather->_color = RED;
					}
				}

			}
			else
			{
				//    g
				//  u   p
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_color == RED)//舅舅存在且为红
				{
					parent->_color = uncle->_color = BLACK;
					grandfather->_color = RED;

					//继续向上更新
					cur = grandfather;
					parent = grandfather->_parent;
				}
				else//舅舅不存在或舅舅为黑
				{
					//     g
					//   u   p
					//		   c
					//单旋+变色
					if (parent->_right == cur)
					{
						RotateL(grandfather);
						parent->_color = BLACK;
						grandfather->_color = RED;
					}
					//     g
					//   u   p
					//     c
					//双旋+变色
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_color = BLACK;
						grandfather->_color = RED;
					}
				}
			}

		}

		//保证了根节点一定为黑
		_root->_color = BLACK;
		return true;
	}

1.2.3 迭代器

红黑树的迭代器较为复杂，其为双向迭代器，因此我们实现一个类，来模拟迭代器的功能。

众所周知，迭代器分为iterator和const_iterator，照例我们应使用两个类来实现，但是我们根据泛型编程思想可以实现一个模板，通过传入不同参数来实现不同的迭代器。

我们用struct来来实现结构体而非class，因为struct默认所有成员都是公有的，这也是为了迭代器这个类能够被封装进红黑树，这点其实也不违背封装的思想

	using Node = RBTreeNode<T>;
	using Self = RBTreeIterator<T, Ref, Ptr>;

1.2.3.1 迭代器的初始化

首先我们需要定义出一个node节点，用于对后续一系列的操作。

其次我们还需一个root节点，记录根节点的位置，至于这是为何，在后续会有讲解。

template<class T,class Ref,class Ptr>//体现泛型编程思想，后续会有讲解
struct RBTreeIterator
{	
    Node* _node;
	Node* _root;

	RBTreeIterator(Node* node,Node* root)
		:_node(node)
		,_root(root)
	{}
}

1.2.3.2 前置++

迭代器++的核⼼逻辑就是不看全局，只看局部，只考虑当前中序局部要访问的下⼀个结点。

若当前节点的右子树不为空，则访问当前节点的右子树中的最左节点。（类似于二叉搜索树的删除）

若当前节点右子树为空，则说明以当前节点为根的树已经没有更大的了，则需往上遍历。此时我们需要定义出cur和parent指针，记录下当前节点和其父亲节点的位置，因为若cur为parnet的右节点，那么根据二叉搜索树的性质可以得知，parent节点对应的值还是比cur的值小，因此还需继续向上遍历，直到cur为parent的左节点。因为这是parent的值才比cur大，我们将其赋值给node节点，并返回迭代器本身。

	Self operator++()
	{
		if (_node->_right)
		{
			// 右不为空，中序下一个访问的节点是右子树的最左(最小)节点
			Node* min = _node->_right;
			while (min->_left)
			{
				min = min->_left;
			}

			_node = min;
		}
		else
		{
			// 右为空，访问祖先里面孩子是父亲左的那个祖先
			Node* cur = _node;
			Node* parent = cur->_parent;

			while ( parent &&  cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			
			_node = parent;
		}

		return *this;
	}

1.2.3.3 前置- -

• • 的逻辑与++大致类似。

若当前节点的左子树不为空，则找其左子树中的最右节点。

若当前节点的左子树为空，则向上搜索，若cur为parent的左节点则继续向上搜索，若cur为parent的右节点则搜索完毕退出循环，将parent节点赋值给node，返回Self

需要注意的是，若操作元素是end（）时，我们若要对其进行--，但end（）迭代器指向的是nullptr，因此这种情况要单独讨论，我们知道- - end到达的是map的最后一个元素

但nullptr我们无法找到其元素，因此这也是为何我们在实现迭代器类到时候，定义了一个成员变量root，用于记录根节点的位置，这样便可以通过这个成员变量遍历map找到最后一个位置并返回。

	Self operator--()
	{
		if (_node == nullptr)
		{
			//即迭代器为end()的位置，此时进行--end()即为最后应该位置,因此需要_root节点记录根从而                    
              进行遍历
			Node* rightMost = _root;
			while (rightMost->_right)
			{
				rightMost = rightMost->_right;
			}
			_node = rightMost;
		}
		else if (_node->_left)
		{
			Node* max = _node->_left;
			while (max->_right)
			{
				max = max->_right;
			}
			_node = max;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}

1.2.3.4 * / -> / != / ==

这三者相对好理解，因此放在一块讲

* 自然是解引用

重载 " * " 我们只需返回其数据即可，而此处百年体现出来泛型编程的思想，若是普通迭代器iterator，此处返回的则是T& ，而若是const迭代器const_iterator则需要返回const T&，因此我们将返回参数设为模板参数之一的Ref，这样就可以在模板实例化时候提供传T& 或者是从const T& 来分别生成对应的迭代器

	Ref operator*()
	{
		return _node->_data;
	}

-> 的重载则是返回节点中数据的地址

这是为什么呢？因为在调用重载的 -> 时候其实是使用了两次 ->

it->first //it.operator->() ->first

因此我们返回的是数据的地址，同样的根据返回值的不同会生成不同的迭代器，因此为什么将返回值设为模板参数之一的Ptr，根据模板实例化时候传入的参数生成对应的迭代器。

	Ptr operator->()
	{
		return &_node->_data;
	}

!= 和 ==我们只需比较节点的地址即可

	bool operator!=(const Self& s) const
	{
		return _node != s._node;
	}
	bool operator==(const Self& s) const
	{
		return _node == s._node;
	}

1.2.3.5 将迭代器封装进红黑树

如此一来，RBTreeIterator这个类我们已经大致模拟出了迭代器的功能，而后便是将其封装进红黑树的结构中

class RBTree
{
public:
	using Node = RBTreeNode<T>;

    //通过模板实例化出不同的类，模拟迭代器
	using Iterator = RBTreeIterator<T, T&, T*>;
	using ConstIterator = RBTreeIterator<T, const T&, const T*>;
        
    。。。
private:
	Node* _root = nullptr;
}

1.3 封装set

由于在复用红黑树框架的时候，我们已经将大致的功能实现好了，如今只需实例化利用红黑树的模板实例化出对应的节点即可。

namespace myset
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& K)
			{
				return K;
			}
		};
	public:
        //封装红黑树的迭代器
		using iterator = typename RBTree<K, const K, SetKeyOfT>::Iterator;
		using const_iterator = typename RBTree<K, const K, SetKeyOfT>::ConstIterator;

		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		const_iterator begin() const
		{
			return _t.begin();
		}
		const_iterator end() const
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const K& k)
		{
			return _t.Insert(k);
		}
	private:
		RBTree<K, const K, SetKeyOfT> _t;
	};
}

1.4 封装map

map比set要多一个功能，即 [ ] 索引功能。

要实现这个功能，我们就需要再map类中重载 [ ]

这里就需要复习一下我们再之前博客中介绍的map功能了

当map中没有对应的键名时候，[ ] 的功能便充当了插入的功能，而若其中已有对应的键名时，其便充当了修改的功能。

那么如何实现呢，先前介绍map的博客也提到过了，使用insert。我们先前实现的insert功能返回值为bool类型，无法满足现在的需求。使用我们要将其返回类型设为pair< iterator , bool > 类型。这样吧能很好的满足需求

当插入失败时候，说明已存在相应的键名，我们的pair类型便返回对应的迭代器位置，以及false，若插入成功则返回插入元素的位置以及true。

在map中实现operator [ ] 的时候我们只需要定义一个pair< iterator , bool > 的变量ret，调用insert函数传入值。若并返回ret.first->second

ret.first指的是插入的元素的所在位置，其是一个迭代器，再调用ret.first->second这里的->便是我们在迭代器类中重载的运算符，目的是取出pair类型的second元素，也可以理解为键值。最后再传引用返回，这样重载的 [ ] 便可以实现修改数据的功能。

namespace mymap
{
	template<class K,class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		using iterator = typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator ;
		using const_iterator =typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator ;
		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		const_iterator begin() const
		{
			return _t.begin();
		}
		const_iterator end() const
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const pair<K,V>& kv)
		{
			return _t.Insert(kv);
		}
		V& operator[](const K& k)
		{
			pair<iterator, bool> ret = insert({ k,V() });
			return ret.first->second;
		}
	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};
}

2. 遇到的问题与经验总结

map和set的封装可以算是目前最难的知识点了，在实现的过程中，我也遭遇了许多困境，其中涉及了众多的知识点，我将其罗列出来并进行总结

2.1 权限放大

以上我在定义RBRreeNode节点的时候，在其初始化函数中我并没有加上const保护，所以出现了以下的报错

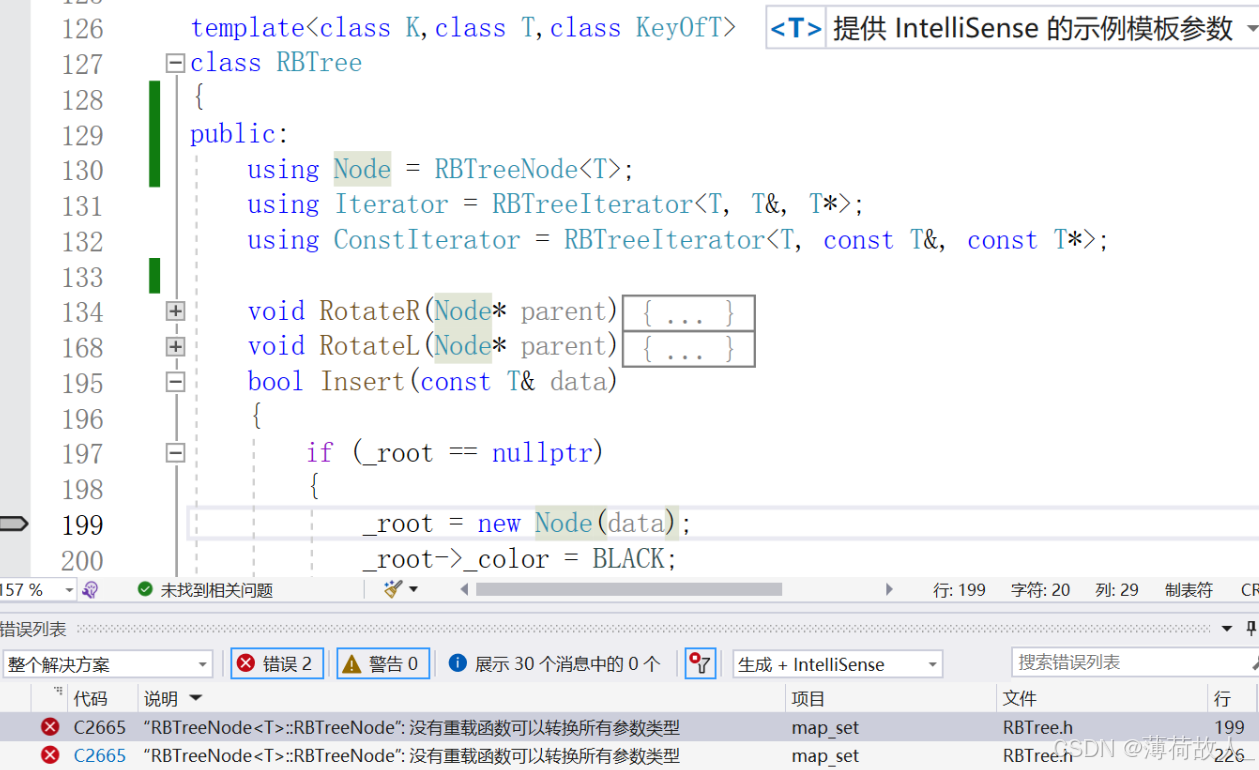
而在实现Insert函数时候，这个地方的data是const修饰的，传入给Node的时候，也是const的，所以Node的构造函数也要是const的接受，不然就会存在权限放大的问题

​​​​​​​ ​​​​​​​ ​​​​​​​

2.2 大量报错

在编写长代码的时候一定要写好一个功能模块就编译一下，否则在最后一股运行就会出现大量的报错。

以至于我一个报错改好之后再次运行突然多了100个报错。。。

所以我们一定要勤测试。

2.3 熟练度不足

初次实现的时候还是磕磕绊绊，需要时不时看一眼源码，并且一开始再这里我卡了很长的一段时间，不过感慨的是，没想到自己从一个c语言不会的菜鸟到现在可以模拟实现了红黑树，以及用来封装map_set,其实写这两篇博客的时候是我抗拒心理最严重的时候，就是因为难，因为不熟练

但其实老话说得好，当你觉得难道时候就在走上坡路的时候，报错了不要怕，要敢于面对，并纠正总结错误，其实生活也是一样，当我们处于人生的低谷时，希望大家都能振作起来，我相信上天不会亏待每一个努力的人的。

祝 前程似锦！

3.源码

RBTree.h

#pragma once
#include<iostream>
#include<vector>
using namespace std;

enum Color
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Color _color;

	RBTreeNode(const T& data)
		:_data(data)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{}

};
template<class T,class Ref,class Ptr>
struct RBTreeIterator
{
	using Node = RBTreeNode<T>;
	using Self = RBTreeIterator<T, Ref, Ptr>;

	Node* _node;
	Node* _root;

	RBTreeIterator(Node* node,Node* root)
		:_node(node)
		,_root(root)
	{}

	Self operator++()
	{
		if (_node->_right)
		{
			// 右不为空，中序下一个访问的节点是右子树的最左(最小)节点
			Node* min = _node->_right;
			while (min->_left)
			{
				min = min->_left;
			}

			_node = min;
		}
		else
		{
			// 右为空，访问祖先里面孩子是父亲左的那个祖先
			Node* cur = _node;
			Node* parent = cur->_parent;

			while ( parent &&  cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			
			_node = parent;
		}

		return *this;
	}
	Self operator--()
	{
		if (_node == nullptr)
		{
			//即迭代器为end()的位置，此时进行--end()即为最后应该位置,因此需要_root节点记录根从而进行遍历
			Node* rightMost = _root;
			while (rightMost->_right)
			{
				rightMost = rightMost->_right;
			}
			_node = rightMost;
		}
		else if (_node->_left)
		{
			Node* max = _node->_left;
			while (max->_right)
			{
				max = max->_right;
			}
			_node = max;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return &_node->_data;
	}
	bool operator!=(const Self& s) const
	{
		return _node != s._node;
	}
	bool operator==(const Self& s) const
	{
		return _node == s._node;
	}
};


template<class K,class T,class KeyOfT>
class RBTree
{
public:
	using Node = RBTreeNode<T>;
	using Iterator = RBTreeIterator<T, T&, T*>;
	using ConstIterator = RBTreeIterator<T, const T&, const T*>;

	void RotateR(Node* parent)
	{
		Node* SubLNode = parent->_left;
		Node* SubLRNode = SubLNode->_right;

		parent->_left = SubLRNode;
		SubLNode->_right = parent;

		//定义PPNode保存parent的父亲节点，避免其被后续操作覆盖导致avl断开
		Node* PPNode = parent->_parent;

		parent->_parent = SubLNode;
		//防止parent为头节点，导致该操作造成空指针的解引用
		if (SubLRNode)
			SubLRNode->_parent = parent;

		if (PPNode == nullptr)
		{
			_root = SubLNode;
			SubLNode->_parent = nullptr;
		}
		else
		{
			if (PPNode->_left == parent)
			{
				PPNode->_left = SubLNode;
			}
			else
			{
				PPNode->_right = SubLNode;
			}
			SubLNode->_parent = PPNode;
		}
	}
	void RotateL(Node* parent)
	{
		Node* SubRNode = parent->_right;
		Node* SubRLNode = SubRNode->_left;
		Node* PPNode = parent->_parent;

		SubRNode->_left = parent;
		parent->_parent = SubRNode;

		parent->_right = SubRLNode;
		if (SubRLNode)
			SubRLNode->_parent = parent;

		if (PPNode == nullptr)
		{
			_root = SubRNode;
			SubRNode->_parent = nullptr;
		}
		else
		{
			if (PPNode->_left == parent)
				PPNode->_left = SubRNode;
			else
				PPNode->_right = SubRNode;
			SubRNode->_parent = PPNode;
		}
	}
	pair<Iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_color = BLACK;

			return pair<Iterator, bool>(Iterator(_root, _root), true);
		}

		KeyOfT kot;
		Node* parent = _root;
		Node* cur = _root;
		while (cur)
		{
			if (kot(data) < kot(cur->_data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(data) > kot(cur->_data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//走隐式类型准换
				//相当于pair<Iterator,bool>(Iterator(cur, _root),false)
				return { Iterator(cur, _root), false };
			}
		}

		//找到节点位置,连接起来
		cur = new Node(data);
		cur->_parent = parent;
		cur->_color = RED;

		//记录插入位置，用于返回值
		//防止cur向上变色丢失插入位置
		Node* newnode = cur;
		if (kot(data) < kot(parent->_data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		
		//父亲节点为红，出现了连续的红色节点，需要进行处理
		//循环处理，直到头节点或父节点为黑
		while (parent && parent->_color == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				//    g
				//  p   u
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_color == RED)//舅舅存在且为红
				{
					parent->_color = uncle->_color = BLACK;
					grandfather->_color = RED;
					
					//继续向上更新
					cur = grandfather;
					parent = grandfather->_parent;
				}
				else//舅舅不存在或舅舅为黑
				{
					//     g
					//   p   u
					//c
					//单旋+变色
					if (parent->_left == cur)
					{
						RotateR(grandfather);
						parent->_color = BLACK;
						grandfather->_color = RED;
					}
					//     g
					//   p   u
					//     c
					//双旋+变色
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_color = BLACK;
						grandfather->_color = RED;
					}
				}

			}
			else
			{
				//    g
				//  u   p
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_color == RED)//舅舅存在且为红
				{
					parent->_color = uncle->_color = BLACK;
					grandfather->_color = RED;

					//继续向上更新
					cur = grandfather;
					parent = grandfather->_parent;
				}
				else//舅舅不存在或舅舅为黑
				{
					//     g
					//   u   p
					//		   c
					//单旋+变色
					if (parent->_right == cur)
					{
						RotateL(grandfather);
						parent->_color = BLACK;
						grandfather->_color = RED;
					}
					//     g
					//   u   p
					//     c
					//双旋+变色
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_color = BLACK;
						grandfather->_color = RED;
					}
				}
			}

		}

		//保证了根节点一定为黑
		_root->_color = BLACK;
		return pair<Iterator,bool>(Iterator(newnode,_root),true);
	}
	bool Check()
	{
		if (_root == nullptr)
			return true;
		if (_root->_color == RED)
			return false;

		int refNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_color == BLACK)
			{
				refNum++;
			}
			cur = cur->_left;
		}

		return  _Check(_root, 0, refNum);
	}
	Iterator begin()
	{
		Node* cur = _root;
		while (cur->_left)
		{
			cur = cur->_left;
		}

		//调用Iterator这个类的构造函数产生新的迭代器位置并返回
		return Iterator(cur,_root);
	}
	Iterator end()
	{
		return Iterator(nullptr,_root);
	}
	ConstIterator begin() const
	{
		Node* cur = _root;
		while (cur->_left)
		{
			cur = cur->_left;
		}

		return ConstIterator(cur,_root);
	}
	ConstIterator end() const
	{
		return ConstIterator(nullptr,_root);
	}
private:
	bool _Check(Node* root, int blackNum, int refNum)
	{
		if (root == nullptr)
		{
			//一条路径走完了
			if (refNum != blackNum)
			{
				cout << "存在黑色结点的数量不相等的路径" << endl;
				return false;
			}

			return true;
		}
		
		//检查孩子不方便，因为孩子有两个，所以反过来检查父亲
		if (root->_color == RED && root->_parent->_color == RED)
		{
			cout << "存在连续的红色结点" << endl;
			return false;
		}
		
		if (root->_color == BLACK)
		{
			blackNum++;
		}

		return _Check(root->_left, blackNum, refNum)
			&& _Check(root->_right, blackNum, refNum);
	}
	Node* _root = nullptr;
};

mymap.h

#pragma once
#include"RBTree.h"

namespace mymap
{
	template<class K,class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		using iterator = typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator ;
		using const_iterator =typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator ;
		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		const_iterator begin() const
		{
			return _t.begin();
		}
		const_iterator end() const
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const pair<K,V>& kv)
		{
			return _t.Insert(kv);
		}
		V& operator[](const K& k)
		{
			pair<iterator, bool> ret = insert({ k,V() });
			return ret.first->second;
		}
	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};
}

myset.h

#pragma once
#include"RBTree.h"

namespace myset
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& K)
			{
				return K;
			}
		};
	public:
		using iterator = typename RBTree<K, const K, SetKeyOfT>::Iterator;
		using const_iterator = typename RBTree<K, const K, SetKeyOfT>::ConstIterator;

		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		const_iterator begin() const
		{
			return _t.begin();
		}
		const_iterator end() const
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const K& k)
		{
			return _t.Insert(k);
		}
	private:
		RBTree<K, const K, SetKeyOfT> _t;
	};
}