精确算法\] 高斯消元法求线性方程组 ## 线性方程组 考虑线性方程组, 已知 A ∈ R n , n , b ∈ R n A\\in \\mathbb{R}\^{n,n},b\\in \\mathbb{R}\^n A∈Rn,n,b∈Rn, 求未知 x ∈ R n x\\in \\mathbb{R}\^n x∈Rn A 1 , 1 x 1 + A 1 , 2 x 2 + ⋯ + A 1 , n x n = b 1 , A_{1,1} x_1 +A_{1,2}x_2+\\cdots +A_{1,n} x_n = b_1, A1,1x1+A1,2x2+⋯+A1,nxn=b1, A 2 , 1 x 1 + A 2 , 2 x 2 + ⋯ + A 2 , n x n = b 2 , A_{2,1} x_1 +A_{2,2}x_2 +\\cdots +A_{2,n} x_n = b_2, A2,1x1+A2,2x2+⋯+A2,nxn=b2, ⋯ \\cdots ⋯ A n , 1 x 1 + A n , 2 x 2 + ⋯ + A n , n x n = b n , A_{n,1} x_1 +A_{n,2}x_2 +\\cdots +A_{n,n} x_n = b_n, An,1x1+An,2x2+⋯+An,nxn=bn, 也可以写为矩阵乘法的形式, A x = b Ax=b Ax=b ## 化为上三角 * 第 1 轮: A i , 1 : n = A i , 1 : n − A i , 1 A 1 , 1 A 1 , 1 : n , i = 2 , ⋯ , n A_{i,1:n} = A_{i,1:n}- \\frac{A_{i,1}}{A_{1,1}} A_{1,1:n}, i=2,\\cdots,n Ai,1:n=Ai,1:n−A1,1Ai,1A1,1:n,i=2,⋯,n * 第 2 轮: A i , 2 : n = A i , 2 : n − A i , 2 A 2 , 2 A 2 , 2 : n , i = 3 , ⋯ , n A_{i,2:n} = A_{i,2:n}- \\frac{A_{i,2}}{A_{2,2}} A_{2,2:n}, i=3,\\cdots,n Ai,2:n=Ai,2:n−A2,2Ai,2A2,2:n,i=3,⋯,n ⋯ \\cdots ⋯ * 第 k 轮: A i , k : n = A i , k : n − A i , k A k , k A k , k : n , i = k + 1 , ⋯ , n A_{i,k:n} = A_{i,k:n}- \\frac{A_{i,k}}{A_{k,k}} A_{k,k:n}, i=k+1,\\cdots,n Ai,k:n=Ai,k:n−Ak,kAi,kAk,k:n,i=k+1,⋯,n * 第n-1 轮 A i , n − 1 : n = A i , n − 1 : n − A i , n − 1 A n − 1 , n − 1 A n , n − 1 : n , i = n A_{i,n-1:n} = A_{i,n-1:n} - \\frac{A_{i, n-1}}{A_{n-1,n-1}} A_{n,n-1:n}, i=n Ai,n−1:n=Ai,n−1:n−An−1,n−1Ai,n−1An,n−1:n,i=n ## 化为对角 * 第 1 轮: A i , 2 : n = A i , 2 : n − A i , n A n , n A n , 2 : n , i = 1 , ⋯ , n − 1 A_{i,2:n} = A_{i,2:n}- \\frac{A_{i,n}}{A_{n,n}} A_{n,2:n}, i=1,\\cdots,n-1 Ai,2:n=Ai,2:n−An,nAi,nAn,2:n,i=1,⋯,n−1 * 第 2 轮: A i , 2 : n − 1 = A i , 2 : n − 1 − A i , n − 1 A n − 1 , n − 1 A n − 1 , 2 : n − 1 , i = 1 , ⋯ , n − 2 A_{i,2:n-1} = A_{i,2:n-1}- \\frac{A_{i,n-1}}{A_{n-1,n-1}} A_{n-1,2:n-1}, i=1,\\cdots,n-2 Ai,2:n−1=Ai,2:n−1−An−1,n−1Ai,n−1An−1,2:n−1,i=1,⋯,n−2 ⋯ \\cdots ⋯ * 第 k 轮: A i , 2 : n − k + 1 = A i , 2 : n − k + 1 − A i , n − k + 1 A n − k + 1 , n − k + 1 A n − k + 1 , 2 : n − k + 1 , i = 1 , ⋯ , n − k + 1 A_{i,2:n-k+1} = A_{i,2:n-k+1}- \\frac{A_{i,n-k+1}}{A_{n-k+1,n-k+1}} A_{n-k+1,2:n-k+1}, i=1,\\cdots,n-k+1 Ai,2:n−k+1=Ai,2:n−k+1−An−k+1,n−k+1Ai,n−k+1An−k+1,2:n−k+1,i=1,⋯,n−k+1 * 第n-1 轮 A i , 2 = A i , 2 − A i , 2 A 2 , 2 A 2 , 2 , i = 1 A_{i,2} = A_{i,2} - \\frac{A_{i, 2}}{A_{2,2}} A_{2,2}, i=1 Ai,2=Ai,2−A2,2Ai,2A2,2,i=1 ## 美化数据格式 ```julia using DataFrames function pm(A,b) m,n=size(A); z=[] for i=1:n z=[z; "a$i"] end z=[z; "b"] println(DataFrame([A b],z)) end ``` ## 高斯消元法程序 ```julia function LEsol(A,b,SHOW=false) """ SHOW 默认为 false 不输出解题步骤, 可以选填 true 输出解题步骤 """ n=length(b); A=copy(A); b=copy(b) if SHOW pm(A,b) end if SHOW println("化为上三角") end for i=1:n-1 for j=i+1:n c=A[j,i]/A[i,i] b[j]=b[j]-b[i]*c A[j,i:n]=A[j,i:n]-A[i,i:n]*c end if SHOW pm(A,b) end end if SHOW println("化为对角") end for i=n:-1:2 for j=1:i-1 c=A[j,i]/A[i,i] b[j]=b[j]-b[i]*c A[j,i:n]=A[j,i:n]-A[i,i:n]*c end if SHOW pm(A,b) end end x=copy(b) for j=1:n x[j]=b[j]/A[j,j]; end return(x) end ``` ## 举例 ```julia n=3; A=ones(Rational,n,n) b=ones(Rational,n) for i=1:n-1 A[i,i]=2.0; A[i,i+1]=1.0; A[i+1,i]=1.0; b[i]=i+0.0 end A[n,n]=2.0; b[n]=n; x=LEsol(A,b,true) ``` ## 求解结果 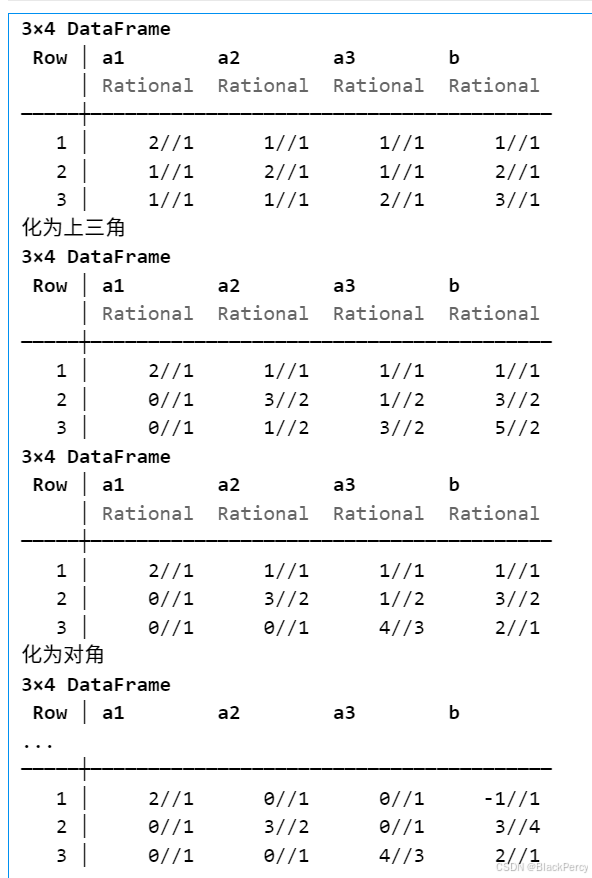
相关推荐
撩妹小狗3 天前
科赫雪花--Python--数学原理--turtle绘图张3蜂3 天前
线性代数与AI的关系AI科技星3 天前
物理世界的几何建构:论统一场论的本体论革命与概念生成super_lzb3 天前
【线性代数】矩阵第一讲:矩阵与矩阵的运算newbiai3 天前
TikTok矩阵账号引流怎么解决效率低成本高?逆境不可逃3 天前
【从零入门23种设计模式08】结构型之组合模式(含电商业务场景)有为少年4 天前
Monarch矩阵:从设计直觉到数学推导与实际应用壹通GEO5 天前
AI-GEO内容矩阵:打造永不枯竭的流量池逆境不可逃6 天前
LeetCode 热题 100 之 73.矩阵置零(含图解)AI科技星7 天前
时空的几何本源与物理现象的建构:论统一场论的宇宙二元论与观察者中心范式