封装红黑树模拟实现map和set

muzi_liii2025-03-29 15:12

文章目录

红黑树如何做到封装两个容器的

map是key/value的搜索场景，set是key的搜索场景，这两个容器的底层，竟然是一致的，这是为什么呢，其实底层的红黑树用了一个巧妙的泛型思想来实现的，红黑树在实现key和key/value的搜索场景时不是写死的，而是由红黑树的第二个模板参数决定结点中存储的数据类型，若红黑树的第二个模板参数传的是key，那就是set的搜索场景，若是键值对，也就是pair<k,v>，那么就是key/value的搜索场景，这样既可以实现key搜索，场景的set，也可以实现key/value场景的map

以下的内容主要是模拟实现几个比较关键的接口

模拟实现map和set的结构

由刚刚的解释我们已经了解到，红黑树为了兼容这两个容器，它不是写死的，而是通过第二个模板参数来决定的，那么用它来模拟实现map和set的结构的代码如下：

cpp 复制代码 
//RBTree.h
#pragma once
#include<iostream>
using namespace std;

enum Colour
{
	RED,
	BLACK
};
template<class T> //该模板参数T决定结点中要存储的数据类型
struct RBTNode
{
	T _date;
	RBTNode<T>* _left;
	RBTNode<T>* _right;
	RBTNode<T>* _parent;
	Colour _col;

	RBTNode(const T& date)
		:_date(date)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{ }
};
template<class K, class T> //若第二个模板参数是key则说明是set容器，若是pair则说明是map容器
class RBTree
{
	typedef RBTNode<T> Node;
public:
	//....
private:
	Node* _root = nullptr;
};

//map.h
#include"RBTree.h"

template<class K, class V>
class map
{
public:
	// ....
private:
	RBTree<K, pair<K,V>> _rbtree; //键值对传给红黑树的结点，进行存储
};

//set.h
#include"RBTree.h"

template<class K>
class set
{
public:
	//...
private:
	RBTree<K, K> _rbtree;//这里的set需要传两次key
};

红黑树的第二个模板参数T已经控制了红黑树结点中存储的数据类型，为什么还要传第一个模板参数key呢，尤其是set，传的两个模板参数都是一样的。我们要注意，在map和set使用find/erase函数时，这两个函数的参数只需要key关键字来进行查找和删除，所以第一个模板参数是传给find/erase等函数作为形参的类型。对于set而言两个参数都是一样的，但对于map而言就完全不一样了，map在insert时是pair对象，但find/ease时是key对象，所以set为了与map兼容，set就需要传两个一样的模板参数

模拟实现map和set的插入函数

map和set的插入函数不是自己自身完成实现的，而是复用了红黑树的插入函数 ，所以在实现map和set的插入函数时，我们得先模拟实现红黑树的insert函数。那么在实现红黑树的插入函数时，我们得解决一个问题，因为红黑树的第二个模板参数是个泛型T，这就导致了，不知道插入的是key还是pair<k,v>，那么insert内部进行插入逻辑比较时，就没办法进行比较，因为pair是默认支持的是key和value一起参与比较的，但是在比较逻辑中我们只需要key参与比较，为解决该问题，我们可以在map和set层分别实现一个MapOfKey和SetOfKey的仿函数传给红黑树的第三个模板参数RbtreeOfT，然后RBTree通过RbtreeOfT仿函数取出T类型对象中的key，再进行比较，具体代码如下：

cpp 复制代码 
//RBTree.h
enum Colour
{
	RED,
	BLACK
};
template<class T> //该模板参数T决定结点中要存储的数据类型
struct RBTNode
{
	T _date;
	RBTNode<T>* _left;
	RBTNode<T>* _right;
	RBTNode<T>* _parent;
	Colour _col;

	RBTNode(const T& date)
		:_date(date)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{ }
};
template<class K, class T,class RBTreeOfKey> //若第二个模板参数是key则说明是set容器，若是pair则说明是map容器
class RBTree
{
	typedef RBTNode<T> Node;
public:
	//进行红黑树的插入方式，只是在此基础上加了个仿函数取关键值进行比较
	bool insert(const T& date)
	{
		if (_root == nullptr)
		{
			_root = new Node(date);
			_root->_col = BLACK;
			return true;
		}
		else
		{
			RBTreeOfKey kot;//创建一个仿函数对象，取key
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				
				if (kot(cur->_date) > kot(date))
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (kot(cur->_date) < kot(date))
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(date);
			cur->_col = RED;
			if (kot(parent->_date) > kot(date))
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}
			cur->_parent = parent;

			while (parent && parent->_col == RED)
			{
				Node* grandfather = parent->_parent;
				if (parent == grandfather->_left)
				{
					Node* uncle = grandfather->_right;
					if (uncle && uncle->_col == RED)
					{
						grandfather->_col = RED;
						parent->_col = uncle->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}
					else
					{
						if (cur == parent->_left)
						{
							//右单旋
							RotateR(grandfather);
							grandfather->_col = RED;
							parent->_col = BLACK;
							break;
						}
						else
						{
							//左右双旋
							RotateL(parent);
							RotateR(grandfather);
							grandfather->_col = RED;
							cur->_col = BLACK;
							break;
						}
					}
				}
				else
				{
					Node* uncle = grandfather->_left;
					if (uncle && uncle->_col == RED)
					{
						grandfather->_col = RED;
						parent->_col = uncle->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}
					else
					{
						if (cur == parent->_right)
						{
							//左单旋
							RotateL(grandfather);
							grandfather->_col = RED;
							parent->_col = BLACK;

							break;
						}
						else
						{
							//右左双旋
							RotateR(parent);
							RotateL(grandfather);
							grandfather->_col = RED;
							cur->_col = BLACK;
							break;
						}
					}
				}
			}
			_root->_col = BLACK;
			return true;
		}
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		Node* pparent = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;
		if (pparent == nullptr)
		{
			_root = subL;
			subL->_parent = pparent;
		}
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = subL;
				subL->_parent = pparent;
			}
			else
			{
				pparent->_right = subL;
				subL->_parent = pparent;
			}
		}
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		Node* pparent = parent->_parent;
		subR->_left = parent;
		parent->_parent = subR;
		if (pparent == nullptr)
		{
			_root = subR;
			subR->_parent = pparent;
		}
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = subR;
			}
			else
			{
				pparent->_right = subR;
			}
			subR->_parent = pparent;
		}
	}
private:

	Node* _root = nullptr;
};

//map.h
template<class K, class V>
class map
{
	struct MapOfKey
	{
		//该仿函数返回pair中的key
		const K& operator()(const pair<K, V>& kv)
		{
			return kv.first;
		}
	};
public:
	bool insert(const pair<K, V>& kv)
	{
		return _rbtree.insert(kv);
	}
private:
	RBTree<K, pair<K,V>,MapOfKey> _rbtree;
};

//set.h
template<class K>
class set
{
	struct SetOfKey
	{
		//该仿函数直接返回key
		const K& operator()(const K& key)
		{
			return key;
		}
	};
public:
	bool insert(const K& key)
	{
		return _rbtree.insert(key);
	}
private:
	RBTree<K, K,SetOfKey> _rbtree;
};

从代码中就可以看到，实现map和set的插入函数很简单，就是对红黑树的插入函数进行复用而已

模拟实现map和set的iterator(迭代器)

iterator的模拟实现，其实很简单，就是用一个类型来封装结点的指针，再通过重载运算符实现迭代器像指针一样访问的行为

模拟实现iterator的难点，就是实现operator++和operator--这两个函数重载，在学习map和set的时候我们就知道，map和set的迭代器走的是中序遍历，也就是左->根->右，那么也就意味着begin()函数返回的是中序的第一个结点

迭代器++的核心逻辑不是看全局，而是看局部，它只考虑当前结点在走中序遍历时要访问的下一个结点，所以，对于operator++的实现，我们可以分三种情况进行分析：

  • 当迭代器指向的结点的右子树不为空时。那就说明当前结点的左子树以及当前结点已经访问完了，所以此时迭代器要访问的下一个结点就是它右子树走中序的第一个结点，也就是右子树的最左结点

    从图中可以看到，当it指向的结点的右子树不为空，说明它的左子树以及当前结点已经访问完了，因为走的是中序遍历，所以it要访问的下一个结点就是右子树的最左结点，所以it就遍历到了图中的15结点
  • 当迭代器指向的结点右子为空且迭代器指向的当前的结点在父结点的左时，那么说明左子树已经访问完了，此时迭代器要访问的下一个结点就是当前结点的父结点

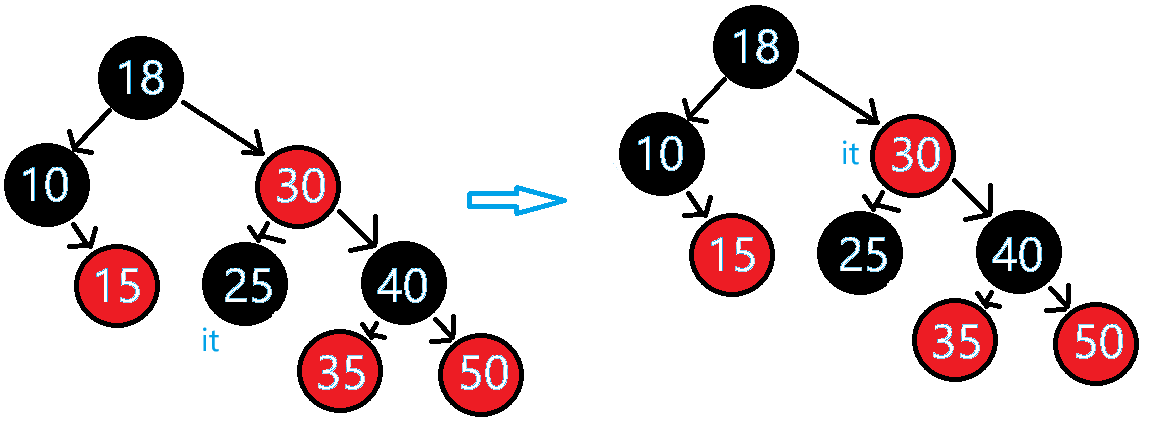
从图中可以看到，it访问的当前结点的右子树为空，且在父结点的左，那么通过中序遍历的逻辑思路，it要访问的下一个结点就是父结点30

  • 若迭代器指向的当前结点的右子树为空且迭代器指向的当前的结点在父结点的右时，意味着当前结点所在的子树已经访问完了，连带着父结点也访问完了，那么迭代器要访问的下一个结点需要继续往父结点的祖先中去找，直到找的的结点是在祖先左边的那个结点，该结点的父结点就是要访问的下一个结点

    图中，迭代器指向的结点的右子树为空，且该结点位于父结点的右，根据中序遍历的逻辑，说明结点10和结点15已经访问完了，那么就需要往上找要访问的下一个结点，往上找之后发现结点10位于祖先的左边，那么要访问的下一个结点即使结点10的父结点，也就是结点18

迭代器中end()函数的实现我们可以直接返回空就可以了，我们可以根据上面的图看到，当访问到最后的50结点时，根据operator++函数的实现，迭代器会往上找结点是在祖先左边的结点，如果若找不到，就会走到根结点的父结点，根的父结点为空，就说明迭代器遍历完了，所以end()函数直接返回一个空的迭代器即可

operator--的实现，与++完全类似，就是在实现时需要将迭代器放置到树的最右边，再根据右->根->左的逻辑，对树进行遍历。那么问题来了，由于我们需要提前将迭代器放置在数的最右结点，那么就需要从根遍历开始找最右结点，所以在迭代器的类中，我们还需要再加一个成员变量来存储根结点

iterator的代码实现如下：

cpp 复制代码 
//RBTree.h
template<class T,class Ref,class Ptr>
struct RBTreeIterator
{
	typedef RBTNode<T> Node;
	typedef RBTreeIterator<T, Ref, Ptr> Self;
	Node* _node;
	Node* _root;
	RBTreeIterator(Node* node,Node* root)
		:_node(node)
		,_root(root)
	{ }

	Ref operator*()
	{
		return _node->_date;
	}
	Ptr operator->()
	{
		return &_node->_date;
	}

	Self& operator++()
	{
		if (_node->_right)//右子树不为空
		{
			Node* moreleft = _node->_right;
			while (moreleft->_left)//找右子树的最左结点
			{
				moreleft = moreleft->_left;
			}
			_node = moreleft;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent->_right == cur)
			{
				//说明该结点的右子树为空且位于父结点的右
				//那么就需要往上找，找到位于祖先左的结点
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}

	Self& operator--()
	{
		if (_node == nullptr)//end()
		{
			//--end(),特殊处理，走到中序最后一个结点，整棵树的最右结点
			Node* moreright = _root;
			while (moreright && moreright->_right)
			{
				moreright = moreright->_right;
			}
			_node = moreright;
		}
		else
		{
			if (_node->_left)
			{
				Node* moreright = _node->_left;
				while (moreright->_right)
				{
					moreright = moreright->_right;
				}
				_node = moreright;
			}
			else
			{
				Node* cur = _node;
				Node* parent = cur->_parent;
				while (parent && parent->_left == cur)
				{
					cur = parent;
					parent = parent->_parent;
				}
				_node = parent;
			}
		}
		return *this;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}
};

template<class K, class T,class RBTreeOfKey> //若第二个模板参数是key则说明是set容器，若是pair则说明是map容器
class RBTree
{
	typedef RBTNode<T> Node;
	
public:
	typedef RBTreeIterator<T, T&, T*> Iterator;
	typedef RBTreeIterator<T, const T&, const T*> ConstIterator;

	Iterator Begin()
	{
		Node* moreleft = _root;
		while (moreleft && moreleft->_left)
		{
			moreleft = moreleft->_left;
		}
		return Iterator(moreleft, _root);
	}
	Iterator End()
	{
		return Iterator(nullptr, _root);
	}

	ConstIterator Begin() const
	{
		Node* moreleft = _root;
		while (moreleft && moreleft->_left)
		{
			moreleft = moreleft->_left;
		}
		return ConstIterator(moreleft, _root);
	}
	ConstIterator End() const 
	{
		return ConstIterator(nullptr, _root);
	}
private:
	Node* _root = nullptr;
};

//map.h
template<class K, class V>
class map
{
	struct MapOfKey
	{
		//该仿函数返回pair中的key
		const K& operator()(const pair<K, V>& kv)
		{
			return kv.first;
		}
	};
public:
	typedef typename RBTree<K, pair<const K, V>, MapOfKey>::Iterator iterator;
	typedef typename RBTree<K, pair<const K, V>, MapOfKey>::ConstIterator const_iterator;
	iterator begin()
	{
		return _rbtree.Begin();
	}
	iterator end()
	{
		return _rbtree.End();
	}
	const_iterator begin() const
	{
		return _rbtree.Begin();
	}
	const_iterator end() const
	{
		return _rbtree.End();
	}
	bool insert(const pair<K, V>& kv)
	{
		return _rbtree.insert(kv);
	}
private:
	RBTree<K, pair<const K,V>,MapOfKey> _rbtree;
};

//set.h
template<class K>
class set
{
	struct SetOfKey
	{
		//该仿函数直接返回key
		const K& operator()(const K& key)
		{
			return key;
		}
	};
public:
	typedef typename RBTree< K,const K, SetOfKey>::Iterator iterator;
	typedef typename RBTree< K,const K, SetOfKey>::ConstIterator const_iterator;
	iterator begin()
	{
		return _rbtree.Begin();
	}
	iterator end()
	{
		return _rbtree.End();
	}
	const_iterator begin() const
	{
		return _rbtree.Begin();
	}
	const_iterator end() const
	{
		return _rbtree.End();
	}
	bool insert(const K& key)
	{
		return _rbtree.insert(key);
	}
private:
	RBTree<K,const K,SetOfKey> _rbtree;
};

还要注意的是，set的iterator不支持修改，我们可以把set的第二个模板参数改成const K即可；而map的iterator不支持修改key但支持修改value，我们可以把map的第二个模板参数paie的第一个参数改成const K即可

模拟实现map的[]

map支持方括号主要需要修改insert的返回值即可，将insert 的返回值修改成：

cpp 复制代码 
pair<iterator,bool> insert(const T& date)

将insert的返回值该成了pair。pair的第二个参数是bool是因为插入右成功也有失败，第二个参数是一个指向要插入的结点的迭代器，当插入成功时，迭代器指向新插入的值的结点的迭代器，插入失败时，迭代器指向已经存在的值的结点的迭代器，说明迭代器始终会指向我们需要插入的那个值的迭代器。所以使得insert函数具有插入和查找的功能，又因为map实现方括号的返回值是value的引用，所以map的方括号具有插入+修改，查找+修改的功能

具体代码实现如下：

cpp 复制代码 
//RBTree.h
pair<Iterator,bool> insert(const T& date)
{
	if (_root == nullptr)
	{
		_root = new Node(date);
		_root->_col = BLACK;
		return make_pair(Iterator(_root, _root), true);
	}
	else
	{
		RBTreeOfKey kot;//创建一个仿函数对象，取key
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			
			if (kot(cur->_date) > kot(date))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(cur->_date) < kot(date))
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//说明插入失败，迭代器指向已经存在的结点
				return make_pair(Iterator(cur, _root), false);
			}
		}
		cur = new Node(date);
		Node* newnode = cur; //由于cur可能会发生改变，所以需要提前记录，便于返回插入的结点
		cur->_col = RED;
		if (kot(parent->_date) > kot(date))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)
				{
					grandfather->_col = RED;
					parent->_col = uncle->_col = BLACK;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_left)
					{
						//右单旋
						RotateR(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
						break;
					}
					else
					{
						//左右双旋
						RotateL(parent);
						RotateR(grandfather);
						grandfather->_col = RED;
						cur->_col = BLACK;
						break;
					}
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					grandfather->_col = RED;
					parent->_col = uncle->_col = BLACK;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_right)
					{
						//左单旋
						RotateL(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;

						break;
					}
					else
					{
						//右左双旋
						RotateR(parent);
						RotateL(grandfather);
						grandfather->_col = RED;
						cur->_col = BLACK;
						break;
					}
				}
			}
		}
		_root->_col = BLACK;
		return make_pair(Iterator(newnode, _root), true);
	}
}

//map.h
V& operator[](const K& key)
{
	pair<iterator, bool> ret = _rbtree.insert(make_pair(key, V()));
	return ret.first->second;
}

因为返回值的pair的迭代器始终指向我们所需要的结点，所以直接返回该迭代器的value值即可

相关推荐
basketball61641 分钟前
C++ STL常用算法之常用排序算法
c++·算法·排序算法
moz与京43 分钟前
[附C++，JS，Python题解] Leetcode 面试150题（10）——轮转数组
c++·python·leetcode
晚雾也有归处3 小时前
链表（C++）
数据结构·c++·链表
勘察加熊人3 小时前
c++实现录音系统
开发语言·c++
李余博睿（新疆）4 小时前
青少年软件编程（C语言）等级考试试卷（三级）
c++
看到我，请让我去学习5 小时前
C语言快速入门-C语言基础知识
c语言·开发语言·c++·vscode
悄悄敲敲敲5 小时前
C++第13届蓝桥杯省b组习题笔记
c++·笔记·算法·蓝桥杯
Non importa6 小时前
【初阶数据结构】线性表之双链表
c语言·开发语言·数据结构·c++·考研·链表·学习方法
学习同学6 小时前
C++初阶知识复习 （31~45）
开发语言·c++
A1-296 小时前
C++的四种类型转换
开发语言·c++
热门推荐
01【笔记】MJ Prompt02DeepSeek各版本说明与优缺点分析03从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑04uniApp使用XR-Frame创建3D场景(3)光源投影的运用。05RAG 实践- Ollama+RagFlow 部署本地知识库06如何在WPS和Word/Excel中直接使用DeepSeek功能07【通信中间件】Fdbus HelloWorld实例08苍穹外卖面试总结09DeepSeek R1本地化部署 Ollama + Chatbox 打造最强 AI 工具10HTML项目一键打包工具：HTML2EXE 最新版