1. 基础绘制

箱线图 是一种用于展示一组数据的五数概括（最小值 、第一四分位数 、中位数 、第三四分位数 和最大值）的图表。

它的几何形态主要由以下几个部分构成：

中位数 （Median）：位于箱体中间的横线，表示数据的中间值，将数据分为上下两部分。
四分位数 （Quartiles）：第一四分位数（Q1）位于箱体下边缘，表示数据中有 25% 的值低于此数；第三四分位数（Q3）位于箱体上边缘，表示数据中有 75% 的值低于此数。
箱体（Box）：由 Q1 和 Q3 构成，其高度表示数据的中间 50% 的分布范围，反映了数据的集中趋势和离散程度。
触须（Whiskers）：从箱体延伸出的两条线，通常表示数据的正常范围。其长度一般为 1.5 倍的四分位距（IQR = Q3 - Q1），超出此范围的数据点被视为异常值。
异常值 （Outliers）：用单独的点标记，表示那些偏离正常范围的数据点，可能需要进一步分析其成因

箱线图的几何形态与数据分布有着密切的关系。例如，

箱体越窄，说明数据的集中程度越高；
触须越短，说明数据的离散程度越小；
异常值的分布情况则可以提示数据中是否存在异常情况或特殊规律。

下面的示例，我们构造一组学生成绩的数据，然后用箱线图来展示成绩的分布情况。

python 复制代码

import plotly.graph_objects as go
import numpy as np

# 生成示例数据
np.random.seed(10)
scores = np.random.randint(1, 100, 100)

# 绘制单变量箱线图
fig = go.Figure(
    data=[
        go.Box(
            y=scores,
            boxpoints="outliers",
        )
    ]
)
fig.update_layout(title="学生考试成绩箱线图", yaxis_title="成绩")
fig.show()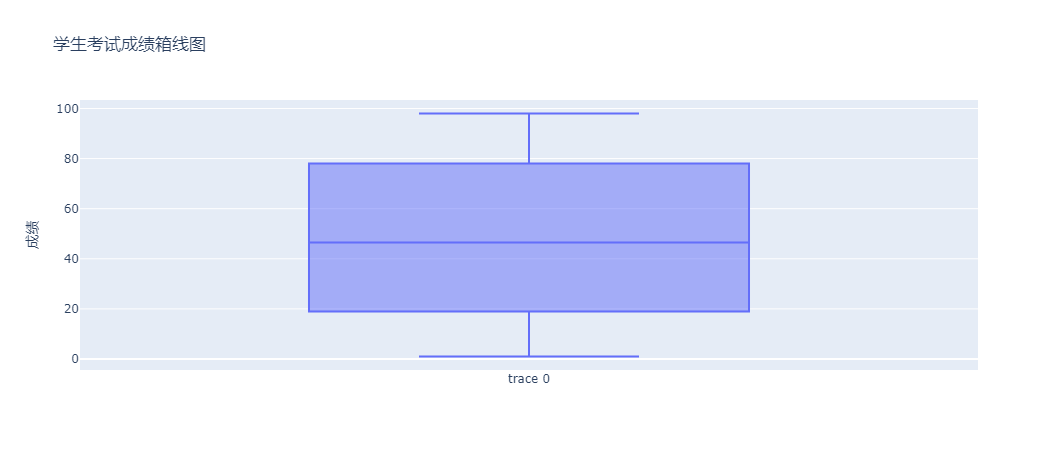

上图中，箱体范围：从 Q1 到 Q3，表示数据的中间 50% 的分布范围。箱体的高度越小，说明数据越集中。

如果有异常值的话，会用蓝色的圆点标记，表示超出正常范围的数据点。

这些异常值可能是数据录入错误、特殊事件影响或其他原因导致的。

比如，我们给变量scores中添加一些异常的数值，再看看箱线图的变化。

python 复制代码

scores = np.append(scores, [-100, 200])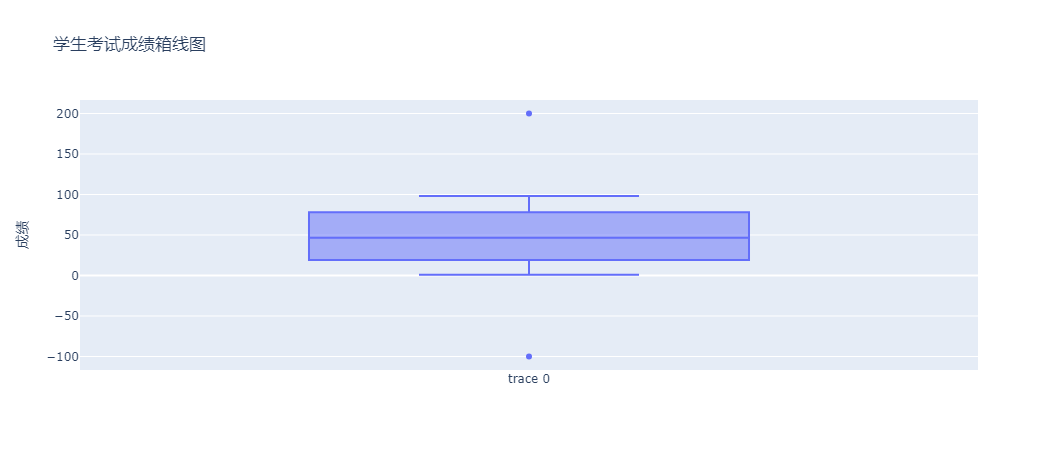

图中多了2个蓝色的圆点，就是后面添加的两个异常值。

2. 分析应用

2.1. 异常值识别

异常值是数据分析中需要特别关注的部分。它们可能会影响统计分析的结果，甚至误导决策。

箱线图提供了一种直观且有效的方法来识别异常值。

异常值通常是通过四分位距（IQR）来判定的。具体规则如下：

小于 $Q1 - 1.5 \\times IQR$ 的数据点被视为下异常值。
大于 $Q3 + 1.5 \\times IQR$ 的数据点被视为上异常值。

Plotly的交互式功能可以让我们更方便地分析异常值。

通过设置boxpoints='all'，我们可以将所有数据点显示出来，并通过颜色或其他样式来区分正常值和异常值。

python 复制代码

import plotly.graph_objects as go
import numpy as np

# 生成示例数据
np.random.seed(10)
scores = np.random.randint(1, 100, 100)
scores = np.append(scores, [-100, 200])

fig = go.Figure(
    data=[
        go.Box(
            y=scores,
            boxpoints="all",
            jitter=0.3,
            pointpos=-1.8,
            marker_color="rgba(0, 0, 255, 0.7)",
            line_color="black",
            notched=True,
        )
    ]
)
fig.update_layout(title="学生考试成绩箱线图（高亮异常值）", yaxis_title="成绩")
fig.show()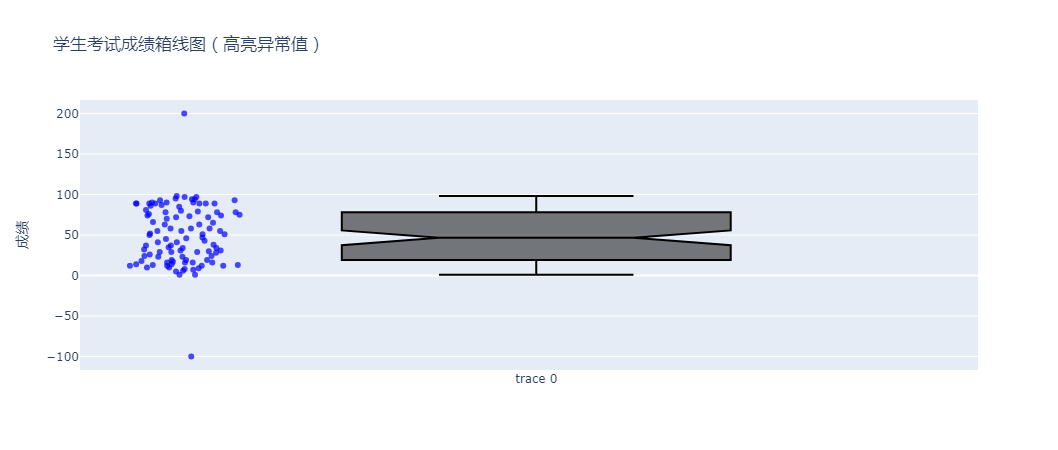

在上述代码中， jitter参数用于调整数据点的抖动程度，避免数据点重叠；

pointpos参数用于控制数据点的水平位置。

通过这种方式，我们可以清晰地看到哪些数据点是异常值。

在识别出异常值后，一般需要根据具体情况选择合适的处理方法：

删除：如果异常值是由于数据录入错误或不可信的测量结果导致的，可以直接将其删除。
修正：如果异常值可能是真实存在的，但数值有误，可以根据业务逻辑或参考其他数据进行修正。
保留：在某些情况下，异常值可能具有重要的业务意义，如特殊事件的影响，此时应保留异常值并进行进一步分析。

2.2. 多组数据箱线图

箱线图不仅可以用于单变量的分析，还可以用于多组数据的对比分析。

通过将不同组的数据绘制在同一张箱线图上，我们可以直观地比较它们的分布特征和差异。

假设我们有一组包含多个分类变量的数据，例如不同班级学生的考试成绩。

python 复制代码

# 示例数据：不同班级学生的考试成绩
data = {
    "Class A": [85, 90, 78, 92, 88, 76, 89, 95, 67, 83],
    "Class B": [82, 87, 79, 91, 85, 75, 88, 93, 77, 84],
    "Class C": [88, 93, 81, 95, 86, 78, 90, 94, 82, 87],
}

fig = go.Figure()
colors = ["blue", "green", "red"]
for class_name, scores in data.items():
    fig.add_trace(
        go.Box(
            y=scores,
            name=class_name,
            boxpoints="outliers",
            line_color="black",
            fillcolor=colors.pop(),
        )
    )

fig.update_layout(
    title="不同班级学生考试成绩对比",
    yaxis_title="成绩",
    xaxis_title="班级",
    boxgap=0.3,
)  # 调整箱线图之间的间距
fig.show()

通过分析分组箱线图，我们可以发现不同班级学生成绩的差异情况。

3. 总结

箱线图作为探索性数据分析中的重要工具，不仅能够帮助我们快速把握数据的分布特征，还能有效识别异常值，促进数据清洗与预处理。

在实际应用中，建议：

优先清洗数据中的极端异常值，避免误导分析结论。
在业务报告中，充分利用箱线图的直观性，传递数据分布与组间差异信息，辅助决策制定。

『Plotly实战指南』--箱线图绘制与应用

1. 基础绘制

2. 分析应用

2.1. 异常值识别

2.2. 多组数据箱线图

3. 总结