股神降临，用LSTM预测股票价格

当人工智能遇见金融市场

股票市场如同一个巨大的信息海洋，无数投资者在其中寻找规律。传统分析方法依赖技术指标与基本面数据，但随着人工智能的发展，一种名为 LSTM（长短期记忆网络） 的深度学习模型，正在为预测股票价格提供新的可能性。本文将以苹果公司（AAPL）的股价为例，手把手教你如何在JupyterLab中搭建LSTM模型，并解释其背后的科学逻辑。即使你没有任何编程经验，也能跟随这篇教程理解核心思想。

LSTM为什么适合预测股价？

1.1 时间序列的"记忆困境"

假设你每天记录气温，想预测明天的温度。最直接的方法是参考最近几天的数据，但极端天气（如寒潮）可能与一个月前的天气模式相关。传统模型难以捕捉这种长期依赖关系，而LSTM通过独特的"门控机制"（输入门、遗忘门、输出门），能自主决定记住或遗忘哪些信息。

1.2 股价预测的特殊挑战

股票价格具有高噪声 （受突发事件影响）、非平稳性 （统计特性随时间变化）和非线性（多个因素复杂交互）的特点。LSTM的优势在于：

能处理时间跨度长的依赖关系
对噪声数据有一定鲁棒性
可自动提取时间序列中的深层特征

1.3 环境准备

首先，确保你已经安装了必要的Python库。你可以使用以下命令来安装所需的库：

复制代码

pip install numpy pandas matplotlib tensorflow scikit-learn yfinance

numpy 和 pandas 用于数据处理。
matplotlib 用于数据可视化。
tensorflow 是深度学习框架，包含LSTM模型。
scikit-learn 用于数据预处理。
yfinance 用于获取股票数据。

数据准备

2.1 获取股票数据

我们使用yfinance库获取苹果公司2010-2025年的历史数据。选择收盘价（Close）作为核心指标，因为它反映每日交易最终共识。

kotlin 复制代码

import yfinance as yf
data = yf.download('AAPL', start='2010-01-01', end='2025-01-01')

2.2 数据预处理三部曲

归一化处理：将价格缩放到0-1区间。这能加速模型收敛，避免大数值主导计算。

ini 复制代码

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(data[['Close']])

时间窗口构建：用过去60天的数据预测第61天。这相当于教模型识别"价格走势模式"。

scss 复制代码

def create_dataset(data, window=60):
    X, y = [], []
    for i in range(len(data)-window-1):
        X.append(data[i:i+window, 0])
        y.append(data[i+window, 0])
    return np.array(X), np.array(y)

维度调整：将数据重塑为LSTM需要的三维格式（样本数, 时间步长, 特征数）。
ini 复制代码
```
X_train = X_train.reshape(X_train.shape[0], 60, 1)
```

构建LSTM模型

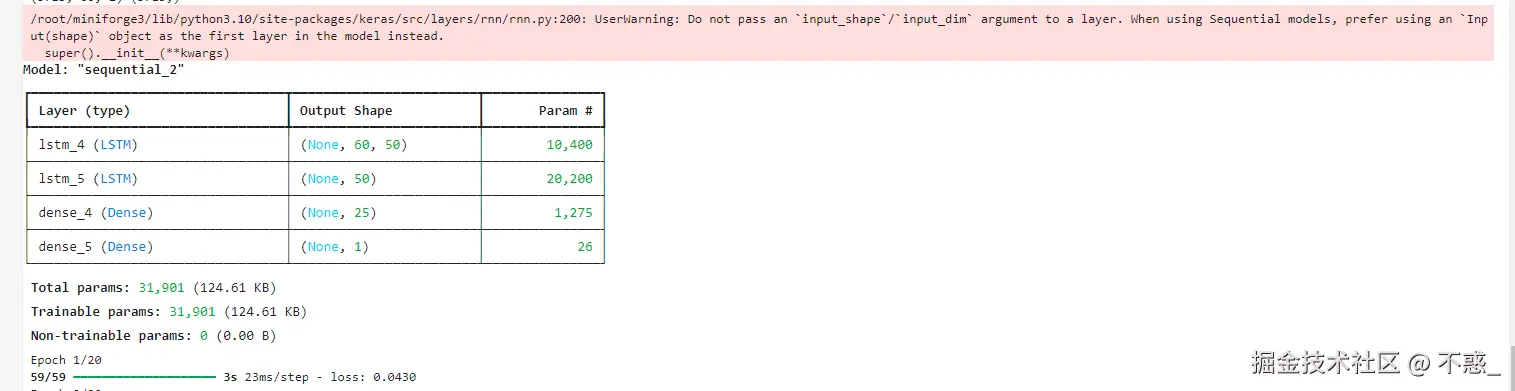
3.1 模型架构解析

第一层LSTM：50个神经元，返回完整序列供下一层使用
第二层LSTM：进一步提取特征，仅返回最终输出
全连接层：将输出映射到预测值

ini 复制代码

model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(60, 1)))
model.add(LSTM(50))
model.add(Dense(1))

3.2 模型训练要点

使用Adam优化器和均方误差损失函数：

Epochs：遍历数据集的次数，并非越大越好（可能过拟合）
Batch Size：每次参数更新使用的样本数，影响训练速度和内存占用

ini 复制代码

model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=20, batch_size=64)

四、预测效果可视化：眼见为实

4.1 训练集拟合效果

虽然预测曲线（橙色）能紧跟实际价格（蓝色），但要警惕过拟合------模型可能只是记住了训练数据，而非学习到通用规律。

4.2 未来30天预测

预测结果呈现平缓上升趋势，这反映模型的两个特性：

对近期趋势的延续性判断
对噪声的平滑处理能力

ini 复制代码

# 预测未来30天价格
future_steps = 30
last_60_days = scaled_data[-time_step:]  # 获取最后60天的数据

# 初始化输入（三维结构）
X_test = last_60_days.reshape(1, time_step, 1)  # 形状 (1, 60, 1)

future_predictions = []



for _ in range(future_steps):
    # 预测下一个时间步
    pred = model.predict(X_test)  # 输出形状 (1, 1)
    future_predictions.append(pred[0, 0])
    
    # 调整预测值维度并拼接到输入序列
    pred_3d = pred.reshape(1, 1, 1)  # 调整为 (1, 1, 1)
    X_test = np.concatenate([X_test[:, 1:, :], pred_3d], axis=1)  # 形状保持 (1, 60, 1)

五、理想与现实的差距

5.1 模型的局限性

黑天鹅事件：新冠疫情等突发事件无法预测
市场有效性：公开信息已反映在股价中
交易成本：预测准确率需超过手续费才有利可图

预测未来，不如理解当下

通过实践，我们不仅学会了一个LSTM模型的搭建方法，更重要的是理解到：在金融市场中，预测的终极价值不在于精准猜中价格，而是通过建模过程洞察市场运作的规律。当你在JupyterLab中看到那条蜿蜒的预测曲线时，它不仅是代码运行的产物，更是人类智慧与机器学习的交响乐章。或许真正的投资智慧，就藏在这种人机协作的探索过程中。

（提示：完整代码如下：）

ini 复制代码

import numpy as np

import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from sklearn.preprocessing import MinMaxScaler

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM

# 获取股票数据
ticker = 'AAPL'
data = yf.download(ticker, start='2010-01-01', end='2025-01-01')

# 查看数据
print(data.head())

# 选择收盘价列
df = data[['Close']]

# 可视化收盘价
plt.figure(figsize=(14,5))

plt.plot(df['Close'])

plt.title(f'{ticker} Stock Price')
plt.xlabel('Date')
plt.ylabel('Price (USD)')
plt.show()

# 归一化
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(df)

# 查看归一化后的数据
print(scaled_data[:5])

# 创建训练数据集
def create_dataset(data, time_step=60):
    X, y = [], []
    for i in range(len(data) - time_step - 1):
        X.append(data[i:(i + time_step), 0])

        y.append(data[i + time_step, 0])
    return np.array(X), np.array(y)

time_step = 60
X_train, y_train = create_dataset(scaled_data, time_step)


# 重塑输入数据为 [samples, time steps, features]
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1], 1)

print(X_train.shape, y_train.shape)

# 构建LSTM模型
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(time_step, 1)))
model.add(LSTM(50, return_sequences=False))
model.add(Dense(25))
model.add(Dense(1))

# 编译模型
model.compile(optimizer='adam', loss='mean_squared_error')

# 查看模型结构
model.summary()


# 训练模型

model.fit(X_train, y_train, batch_size=64, epochs=20)

# 预测训练集
train_predict = model.predict(X_train)

# 反归一化
train_predict = scaler.inverse_transform(train_predict)

y_train = scaler.inverse_transform(y_train.reshape(-1, 1))

# 可视化预测结果
plt.figure(figsize=(14,5))
plt.plot(y_train, label='Actual Price')
plt.plot(train_predict, label='Predicted Price')
plt.title(f'{ticker} Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Price (USD)')
plt.legend()
plt.show()

# 预测未来30天价格
future_steps = 30
last_60_days = scaled_data[-time_step:]  # 获取最后60天的数据

# 初始化输入（三维结构）
X_test = last_60_days.reshape(1, time_step, 1)  # 形状 (1, 60, 1)

future_predictions = []

for _ in range(future_steps):
    # 预测下一个时间步
    pred = model.predict(X_test)  # 输出形状 (1, 1)
    future_predictions.append(pred[0, 0])
    
    # 调整预测值维度并拼接到输入序列
    pred_3d = pred.reshape(1, 1, 1)  # 调整为 (1, 1, 1)
    X_test = np.concatenate([X_test[:, 1:, :], pred_3d], axis=1)  # 形状保持 (1, 60, 1)


# 反归一化
future_predictions = scaler.inverse_transform(np.array(future_predictions).reshape(-1, 1))



# 可视化
plt.figure(figsize=(14,5))
plt.plot(future_predictions, label='Future Predictions')
plt.title(f'{ticker} Future Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Price (USD)')
plt.legend()
plt.show()