决策树剪枝：平衡模型复杂性与泛化能力

在机器学习的世界里，决策树 是一种简单而强大的算法，但它的 "任性生长" 却常常让数据科学家陷入 "过拟合的困境"。

想象一下，一棵决策树如果无限生长，它可能会完美地拟合训练集中的每一个数据点，但当面对新的数据时，却可能表现得像一个"陌生人"------预测完全失效。

这种现象背后的原因在于模型过于复杂，对训练数据的噪声和细节过度拟合，而失去了对新数据的泛化能力。

而剪枝，正是为了解决这一问题而诞生的。

它的核心目标是降低模型的复杂度，让决策树在训练数据和新数据之间找到一个平衡点，从而提升模型的泛化性能。

剪枝的策略主要分为两大流派：预剪枝 和后剪枝。

这两种策略各有优劣，本文中我们将深入探讨它们的原理和应用。

1. 核心概念

1.1. 过拟合

所谓过拟合，就是未剪枝的决策树在训练集上会进行极其复杂的划分，每一个数据点都可能被单独划分到一个区域中。

这种划分虽然在训练集上表现很好，但增加了模型的自由度。

高自由度减少了偏差但增加了方差，使得模型对训练数据的小变化非常敏感，并且在新数据上容易出错。

这就是偏差-方差权衡的关键。

1.2. 剪枝

剪枝的作用机制主要体现在对节点的合并上。

一种是自底向上的合并策略，从叶子节点开始，逐步向上合并那些对模型性能提升不明显的节点；

另一种是直接修剪子树，一次性去掉那些对整体分类效果贡献较小的子树。

在剪枝时，需重新评估信息增益和基尼系数这两个指标，以决定是否合并节点或修剪子树。

这些指标原本用于决策树生长过程中的节点分裂评估。

2. 预剪枝：防患于未然

2.1. 实现原理

预剪枝通过在决策树生长过程中设置一些限制条件，提前终止某些分支的生长。

深度限制 是一种常见的预剪枝方法，通过设置 max_depth 阈值，限制决策树的最大深度，防止树过度生长。

样本量阈值 也是一个重要的参数，min_samples_split 规定了节点分裂所需的最小样本数，min_samples_leaf 则规定了叶子节点所需的最小样本数。

当节点中的样本数小于这些阈值时，节点将不再分裂。

信息增益阈值则是从数学标准的角度出发，当节点分裂带来的信息增益小于某个阈值时，提前终止分裂。

2.2. 实现示例

下面通过构造一些随机的测试数据来演示预剪枝的效果。

首先看看不做预剪枝的效果：

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score

# 生成一个分类数据集
X, y = make_classification(
    n_samples=1000,
    n_features=10,
    n_informative=5,
    n_redundant=0,
    n_clusters_per_class=1,
    random_state=42,
)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 创建一个没有任何限制的决策树分类器
clf = DecisionTreeClassifier(random_state=42)

# 在训练集上训练模型
clf.fit(X_train, y_train)

# 在训练集和测试集上进行预测
y_train_pred = clf.predict(X_train)
y_test_pred = clf.predict(X_test)

# 计算训练集和测试集的准确率
train_accuracy = accuracy_score(y_train, y_train_pred)
test_accuracy = accuracy_score(y_test, y_test_pred)

print(f"训练集准确率: {train_accuracy}")
print(f"测试集准确率: {test_accuracy}")

## 运行结果：
'''
训练集准确率: 1.0
测试集准确率: 0.935
'''

不进行预剪枝 ，在训练集上准确率100%，测试集上准确率93.5%。

把训练后的决策树绘制出来，可以看出，分支非常多。

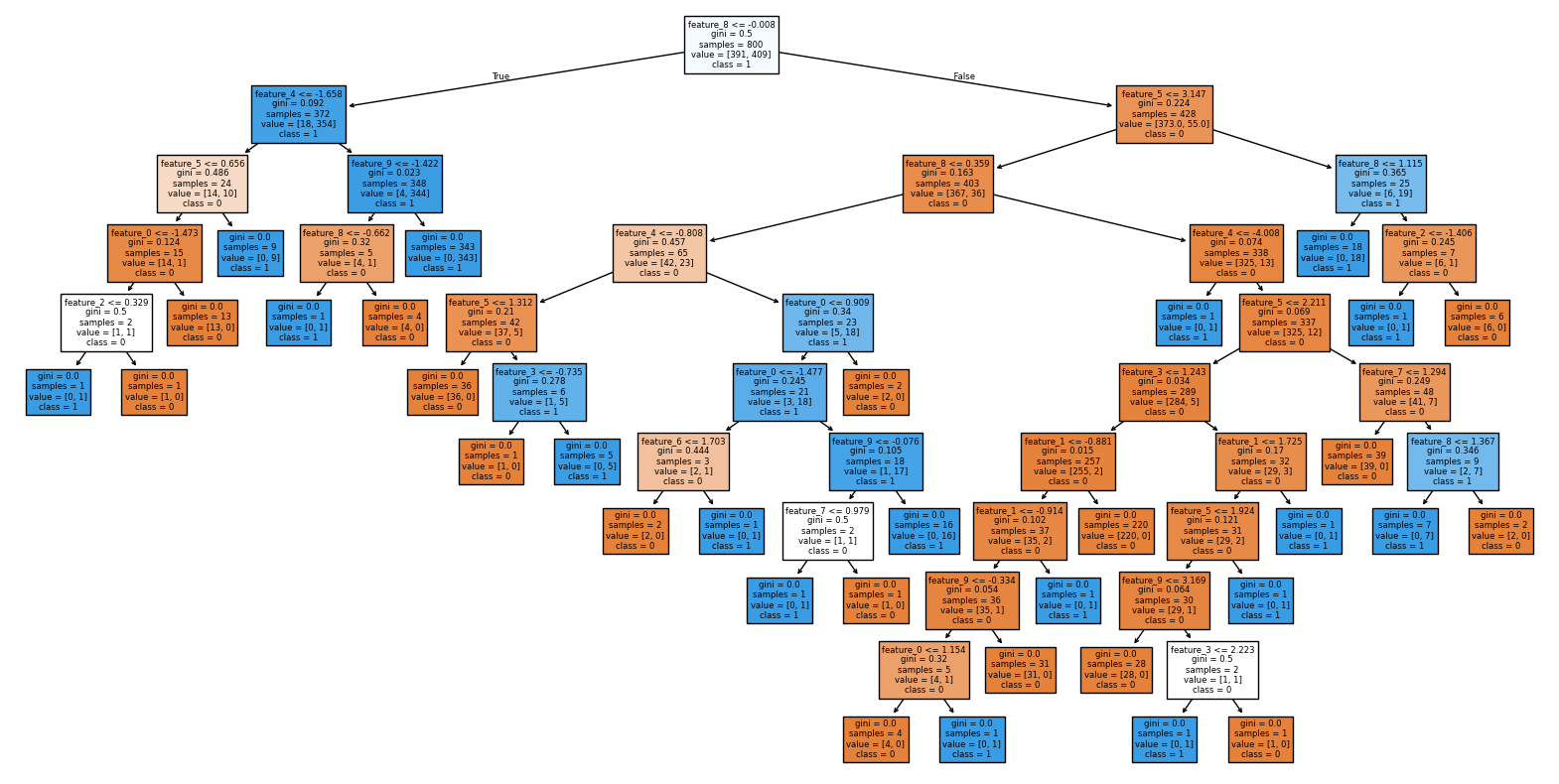
接下来，看看使用预剪枝 的效果，我们通过深度限制 和样本量阈值 参数来实现预剪枝。

代码很简单，只需要修改一行：

# 创建一个没有任何限制的决策树分类器
clf = DecisionTreeClassifier(random_state=42,
                             max_depth=3,
                             min_samples_split=5)

运行之后的结果：

训练集准确率: 0.95125
测试集准确率: 0.955

从准确率上来看，虽然训练集准确率有所降低，但是在测试集上的表现比之前更好，说明泛化能力有提高。

把预剪枝之后的决策树绘制出来，可以看出，分支减少了很多，决策树更加清晰。

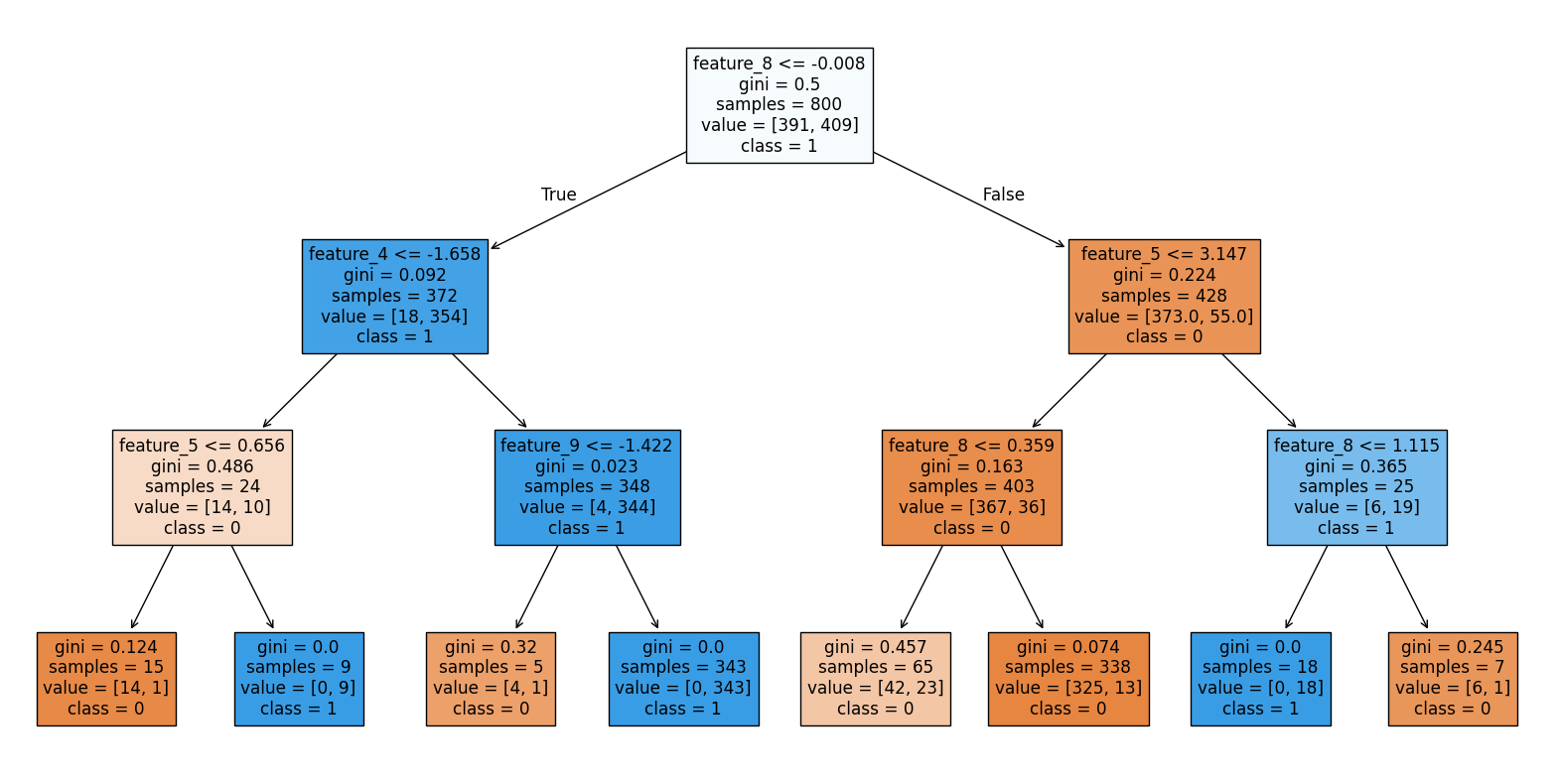
3. 后剪枝：精雕细琢

3.1. 实现原理

后剪枝是在决策树完全生长之后，对树进行剪枝操作。

错误率降低剪枝 （REP）是一种基于验证集的迭代优化算法，它通过不断地剪枝和评估验证集上的错误率，选择错误率最低的剪枝结果。

悲观剪枝 （PEP）则是从统计置信度的角度进行理论推导，通过计算剪枝前后模型在验证集上的性能变化，判断是否应该进行剪枝。

成本复杂度剪枝 （CCP）引入了一个参数 α，通过控制 α 的值来选择要剪枝的子树，α 越大，剪枝越彻底。

3.2. 实现示例

后剪枝是在决策树构建完成后，对树进行修剪以避免过拟合的方法。

在scikit-learn中，可以使用成本复杂度剪枝（Cost Complexity Pruning）来实现后剪枝，它通过控制一个复杂度参数ccp_alpha来完成。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt


# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 计算不同 ccp_alpha 值下的剪枝结果
clf = DecisionTreeClassifier(random_state=42)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

# 存储不同 ccp_alpha 值下的模型
clfs = []
for ccp_alpha in ccp_alphas:
    clf = DecisionTreeClassifier(random_state=42, ccp_alpha=ccp_alpha)
    clf.fit(X_train, y_train)
    clfs.append(clf)

# 移除最后一个模型（因为 ccp_alpha 最大时树为空）
clfs = clfs[:-1]
ccp_alphas = ccp_alphas[:-1]

# 计算不同模型在训练集和测试集上的准确率
train_scores = [clf.score(X_train, y_train) for clf in clfs]
test_scores = [clf.score(X_test, y_test) for clf in clfs]

# 找到测试集准确率最高时的 ccp_alpha 值
best_index = test_scores.index(max(test_scores))
best_ccp_alpha = ccp_alphas[best_index]

# 绘制不同 ccp_alpha 值下训练集和测试集的准确率变化图
fig, ax = plt.subplots()
ax.set_xlabel("alpha值")
ax.set_ylabel("准确率")
ax.set_title("训练集和测试集上的准确率和alpha值")
ax.plot(ccp_alphas, train_scores, marker='o', label="训练集", drawstyle="steps-post")
ax.plot(ccp_alphas, test_scores, marker='o', label="测试集", drawstyle="steps-post")
ax.legend()
plt.show()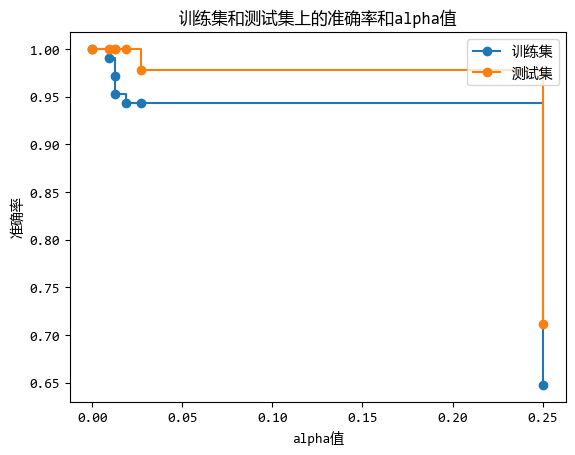

从图中可以看出，ccp_alpha参数设置在0.01附近时，训练集和测试集的准确率都很高。

4. 预剪枝 vs 后剪枝

这两种剪枝方式各有优缺点，它们的比较见下表：

以下是一个对比预剪枝和后剪枝优缺点及应用场景的表格：

	预剪枝	后剪枝
定义	在决策树生长过程中，提前停止树的生长以防止过拟合	在决策树完全生长后，通过剪枝来简化模型，提高泛化能力
优点	1. 计算效率高 ：在树生长过程中进行剪枝，减少了计算量。 2. 防止过拟合 ：通过限制树的生长，有效避免过拟合。 3. 实现简单：参数设置相对直观，易于理解和实现。	1. 模型性能更优 ：在完全生长的树上进行剪枝，能更好地保留有用信息。 2. 灵活性高：可以根据验证集的性能动态调整剪枝策略。
缺点	1. 可能欠拟合 ：过早停止树的生长，可能剪掉一些有用的分支，导致模型欠拟合。 2. 参数敏感：剪枝参数（如深度限制、样本量阈值等）的选择对模型性能影响较大，需要经验调整。	1. 计算复杂度高 ：需要对完全生长的树进行评估和剪枝，计算量较大。 2. 参数选择困难：剪枝参数（如α值）的选择需要多次尝试和验证，增加了调参难度。
应用场景	1. 数据规模较小 ：当数据集较小时，预剪枝可以减少计算量，同时避免过拟合。 2. 对计算效率要求高 ：在需要快速得到模型的情况下，预剪枝是一个不错的选择。 3. 初步探索性分析：在初步探索数据特征时，预剪枝可以快速得到一个大致的模型。	1. 数据规模较大 ：当数据集较大时，后剪枝可以在完全生长的树上进行更精细的剪枝，得到更优的模型。 2. 对模型性能要求高 ：在需要高精度模型的情况下，后剪枝能更好地平衡复杂度和泛化能力。 3. 集成学习：在集成学习方法（如随机森林）中，后剪枝可以提高单个决策树的性能，从而提升整体集成模型的性能。

5. 总结

决策树剪枝是一门在"奥卡姆剃刀"与预测能力之间寻找平衡的艺术。

预剪枝和后剪枝各有优劣，选择哪种策略取决于具体的应用场景和需求。

通过深入理解剪枝的原理和方法，我们可以更好地控制决策树的复杂度，提升模型的泛化能力。

在机器学习的道路上，剪枝只是众多优化手段中的一种，但它却是帮助我们避免过拟合、提升模型性能的重要工具。