深度解析强化学习：原理、算法与实战

- [0. 前言](#0. 前言)
- [1. 强化学习基础](#1. 强化学习基础)
- - [1.1 基本概念](#1.1 基本概念)
  - [1.2 马尔科夫决策过程](#1.2 马尔科夫决策过程)
  - [1.3 目标函数](#1.3 目标函数)
  - [1.4 智能体学习过程](#1.4 智能体学习过程)
- [2. 计算状态值](#2. 计算状态值)
- [3. 计算状态-动作值](#3. 计算状态-动作值)
- [4. Q 学习](#4. Q 学习)
- - [4.1 Q 值](#4.1 Q 值)
  - [4.2 使用 Q 学习进行 frozen lake 游戏](#4.2 使用 Q 学习进行 frozen lake 游戏)
  - [4.3. frozen lake 问题](#4.3. frozen lake 问题)
  - [4.4 实现 Q 学习](#4.4 实现 Q 学习)
- 小结
- 系列链接

0. 前言

强化学习 (Reinforcement learning, RL) 是一种基于行为和心理学的学习形式，试图复制生物通过奖励学习的方式，类似于使用某种形式的奖励(如食物或赞美)训练宠物，强化学习建模对于理解高级意识和人类如何进行学习具有重要作用。本文首先介绍强化学习的基本原理，包括马尔可夫决策过程、价值函数、探索-利用问题等，然后介绍经典的强化学习算法，最后实现在游戏中模拟强化学习算法。

1. 强化学习基础

1.1 基本概念

强化学习 (Reinforcement learning, RL) 是机器学习中的一个重要领域，其核心思想在于最大化智能体在相应环境中得到的累计奖励，重点研究智能体应该如何在给定环境状态下执行动作来最大化累积奖励，从而学习能够令智能体完成目标任务的最佳策略。智能体 (agent) 在每个时刻可以与环境 (environment) 交互，交互过程如下所示：

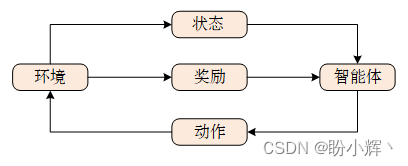
每次交互，都可以得到一个具有多维特征的观察 (observation)，根据观察可以得到状态 (state)，智能体根据状态选择相应的动作 (action)，环境会对 agent 的不同动作给予不同奖励 (reward)，从状态到动作的映射函数称为策略 (policy)。通过重复执行此过程，就可以得到令累计奖励最大化的最佳策略。

例如，在象棋对战中，计算机是一个已经学习或正在学习如何下棋的智能体，游戏的规则设置构成环境，移动棋子(执行动作)后，棋盘中棋子的位置(状态)发生了变化，游戏结束时，智能体根据游戏结果获得奖励，智能体的目标是最大化奖励。

在智能体 (agent1) 与人类进行游戏过程中，它可以进行的游戏是有限的(取决于人类水平)，这可能会成为智能体的学习瓶颈。但是，如果 agent1 (正在学习如何游戏的智能体)可以与 agent2 对战（另一个正在学习的智能体或者一个已经能够出色进行游戏的棋类软件)，从理论上讲，这些智能体就可以无限制的相互博弈，从而最大限度地提高智能体学习玩好游戏的机会。这样，通过在多次游戏上互相博弈，智能体有可能学习如何很好地解决游戏中的不同场景/状态。

1.2 马尔科夫决策过程

智能体从环境初始状态开始，根据策略模型采样某一动作，环境在动作的影响下，会从原状态改变为新状态，同时给予智能体奖励。以上过程不断重复直到达到游戏的终止状态，这个过程也称为轨迹 (trajectory)，一个过程称为一个回合 (episode)。环境的当前状态通常取决于多个历史状态，计算非常复杂，为了简化计算流程，我们通常假设当前时间戳上的状态仅仅受上一状态的影响，这种性质称为马尔科夫性 (Markov Property)，具有马尔科夫性的序列称为马尔科夫过程 (Markov Process)。

如果我们将执行的动作也考虑进状态转移概率，同样应用马尔科夫假设，当前状态只与上一状态和上一状态上执行的动作相关，则我们把状态和动作的有序序列叫做马尔科夫决策过程 (Markov Decision Process, MDP)。当智能体只能观察到环境的部分状态时，称为部分可观察马尔可夫决策过程 (Partially Observable Markov Decision Process , POMDP)

1.3 目标函数

智能体每次在与环境进行交互时，都会得到一个奖励，一次交互轨迹的累计奖励称为总回报 (return)，但在某些环境中的奖励是十分稀疏的，例如在棋牌类游戏中，前面的动作奖励均为 0，只有游戏结束时才有表示输赢的奖励。为了权衡近期奖励与长期奖励，引入折扣率来令奖励随时间衰减。

由于环境状态转移和策略具有一定的随机性，即使使用同样的策略模型作用域同一环境，也可能产生截然不同的轨迹序列，因此强化学习的目标是最大化期望回报。

1.4 智能体学习过程

通常，智能体的学习过程如下：

最初，智能体在给定状态下采取随机动作
智能体将它在游戏中的各种状态下所采取的动作存储在内存中
然后，智能体将各种状态下的动作结果与奖励相关联
在进行多次游戏之后，智能体可以通过重播其经验将一个状态中的动作与潜在奖励相关联

2. 计算状态值

接下来，量化在给定状态下采取动作所对应的值问题，为了理解如何量化一个状态的值，定义环境和目标如下：

环境是一个两行三列的网格，智能体从 start 单元格开始，如果智能体到达右下角的网格单元格，则表示目标实现，智能体得到 +1 的分数奖励；如果智能体到达其他单元格，将无法得到奖励，或者说奖励为 0。智能体可以通过向右、向左、底部或向上移动来执行动作，具体取决于动作的可行性，例如，智能体在起始网格单元格中只能向右或向下移动。

利用这些信息，我们可以计算一个单元格的值(即智能体在所处的状态)。假设从一个单元格移动到另一个单元格需要耗费一定能量，我们使用折扣因子 γ γ γ 表示负责从一个单元格移动到另一个单元格所花费的能量。此外，引入 γ γ γ 可以使智能体更快的进行学习。接下来形式化贝尔曼方程，用于计算单元格的值；

v a l u e o f a c t i o n t a k e n i n a s t a t e = r e w a r d o f m o v i n g t o t h e n e x t c e l l + γ × v a l u e o f t h e b e s t p o s s i b l e a c t i o n i n n e x t s t a t e \begin{aligned} value\ of\ action\ taken\ in\ a\ state&=reward\ of\ moving\ to\ the\ next\ cell + \\ &\gamma\times value\ of\ the\ best\ possible\ action\ in\ next\ state \end{aligned} value of action taken in a state=reward of moving to the next cell+γ×value of the best possible action in next state

根据以上等式，一旦确定了某一状态下的最佳动作，就可以计算所有单元格的值，设 γ γ γ 值为 0.9 0.9 0.9 ( γ γ γ 通常在 0.9 和 0.99 之间)：

V 22 = R 23 + γ × V 23 = 1 + γ × 0 = 1 V 13 = R 23 + γ × V 23 = 1 + γ × 0 = 1 V 21 = R 22 + γ × V 22 = 0 + γ × 1 = 0.9 V 12 = R 13 + γ × V 13 = 1 + γ × 1 = 0.9 V 11 = R 12 + γ × V 12 = 1 + γ × 0.9 = 0.81 V_{22}=R_{23}+\gamma\times V_{23}=1+\gamma\times 0=1 \\ V_{13}=R_{23}+\gamma\times V_{23}=1+\gamma\times 0=1 \\ V_{21}=R_{22}+\gamma\times V_{22}=0+\gamma\times 1=0.9 \\ V_{12}=R_{13}+\gamma\times V_{13}=1+\gamma\times 1= 0.9\\ V_{11}=R_{12}+\gamma\times V_{12}=1+\gamma\times 0.9=0.81 V22=R23+γ×V23=1+γ×0=1V13=R23+γ×V23=1+γ×0=1V21=R22+γ×V22=0+γ×1=0.9V12=R13+γ×V13=1+γ×1=0.9V11=R12+γ×V12=1+γ×0.9=0.81

从以上计算中，我们可以了解如何计算给定单元格(状态)中的值，当给定该状态下的最佳动作时。对于本节所用的简单示例，计算方法如下：

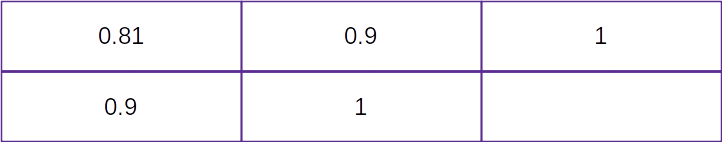
得到这些值后，我们期望智能体能够遵循值增加的路径采取动作。了解了如何计算状态值后，在下一节中，我们将了解如何计算与状态-动作组合相关的值。

3. 计算状态-动作值

在上一节中，我们假设能够预先了解智能体如何获取最优动作，但这在实际场景中并不现实。在本节中，我们将学习如何确定与状态-动作组合对应的值。

如下图所示，单元格中的每个子单元格代表在该单元格中采取动作的值。最初，各种动作的单元格值如下：

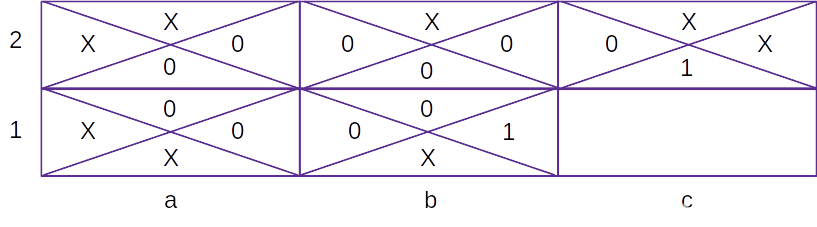
在上图中，如果智能体从 b1 单元格向右移动或从 c2 单元格向下移动，则 b1/c2 单元格的值为 1，而其他动作的值为 0；X 表示该动作不可行，因此没有与之相关联的值。在四次迭代过程中，给定状态下采取不同动作更新单元格值如下：

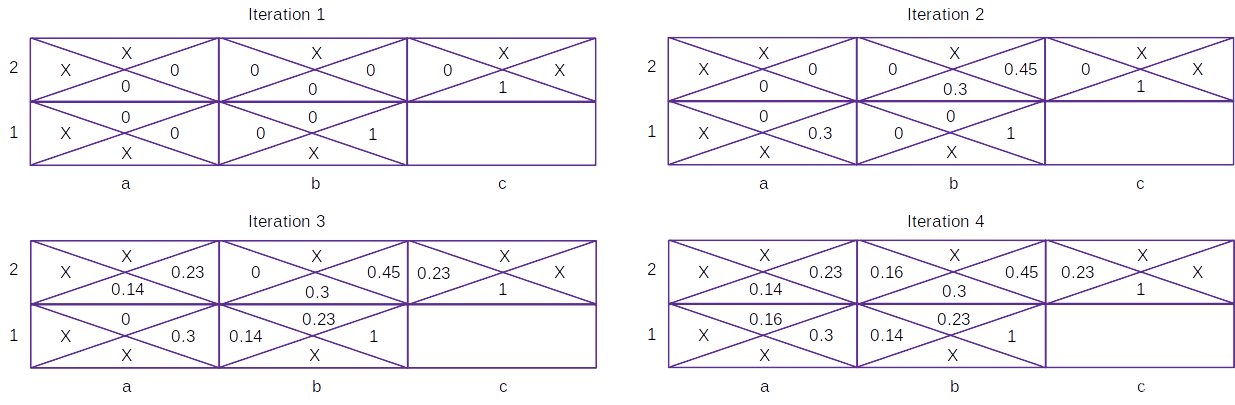
经过多次迭代，以获取使每个单元格的值最大化的最佳操作。

接下来，我们介绍如何计算第二个表 (Iteration2) 中的单元格值。以第二个表中第一行、第二列采取向下动作为例，得到的值为 0.3，当智能体采取向下行动时，它有 1/3 的机会在下一个状态下采取最优动作。因此，采取向下行动的值如下：

v a l u e o f t a k i n g d o w n w a r d a c t i o n = i m m e d i a t e r e w a r d + γ × ( 1 / 3 × 0 + 1 / 3 × 0 + 1 / 3 × 1 ) = 0 + 0.9 × 1 / 3 = 0.3 \begin{aligned} value\ of\ taking\ downward\ action &=immediate\ reward+ \gamma\times (1/3\times 0+1/3\times 0+1/3\times 1)\\ &=0+0.9\times 1/3\\ &=0.3 \end{aligned} value of taking downward action=immediate reward+γ×(1/3×0+1/3×0+1/3×1)=0+0.9×1/3=0.3

以类似的方式，我们可以获得在不同单元格中采取不同可能动作的值。

4. Q 学习

我们已经学习了如何计算所有组合的状态-动作值。从理论上讲，计算了所需要的各种状态-动作值后，就可以确定在每个状态下将采取的动作，但在复杂情况下(例如玩视频游戏)，获取状态信息并不容易。为了能够方便的获取正在进行的游戏的预定义环境，可以使用 OpenAI 的 Gym 环境，使用 Gym 环境可以获取给定当前状态下采取动作后的下一状态信息。虽然，我们一直希望选择最优路径，但在某些情况下，智能体可能会陷入局部最小值。

在本节中，我们将首先介绍 Q 值，学习利用 Q-learning 计算给定状态下动作的值，并介绍如何利用 Gym 环境进行各种游戏。为了避免智能体陷入局部最小值，我们将利用探索-开发技术。

4.1 Q 值

Q 学习 (Q-learning) 中的 Q 值 (Q-value) 表示动作的质量，计算方法如下：

v a l u e o f a c t i o n t a k e n i n a s t a t e = r e w a r d o f m o v i n g t o t h e n e x t c e l l + γ × v a l u e o f t h e b e s t p o s s i b l e a c t i o n i n n e x t s t a t e value\ of\ action\ taken\ in\ a\ state=reward\ of\ moving\ to\ the\ next\ cell + \gamma\times value\ of\ the\ best\ possible\ action\ in\ next\ state value of action taken in a state=reward of moving to the next cell+γ×value of the best possible action in next state

网络需要不断更新给定状态下的状态-动作值，直到达到收敛状态，因此，可以改写以上公式：

v a l u e o f a c t i o n t a k e n i n a s t a t e = V a l u e o f a c t i o n t a k e n i n a s t a t e + 1 × ( r e w a r d o f m o v i n g t o t h e n e x t c e l l + γ × V a l u e o f t h e b e s t p o s s i b l e a c t i o n i n n e x t s t a t e − V a l u e o f a c t i o n t a k e n i n a s t a t e ) \begin{aligned} value\ of\ action\ taken\ in\ a\ state &= Value\ of\ action\ taken\ in\ a\ state + \\ & 1\times (reward\ of\ moving\ to\ the\ next\ cell+\\ & \gamma\times Value\ of\ the\ best\ possible\ action\ in\ next\ state-\\ & Value\ of\ action\ taken\ in\ a\ state) \end{aligned} value of action taken in a state=Value of action taken in a state+1×(reward of moving to the next cell+γ×Value of the best possible action in next state−Value of action taken in a state)

在以上等式中，将 1 替换为学习率，以便可以更稳定的更新在某个状态下采取的动作的值：

v a l u e o f a c t i o n t a k e n i n a s t a t e = V a l u e o f a c t i o n t a k e n i n a s t a t e + l e a r n i n g r a t e × ( r e w a r d o f m o v i n g t o t h e n e x t c e l l + γ × V a l u e o f t h e b e s t p o s s i b l e a c t i o n i n n e x t s t a t e − V a l u e o f a c t i o n t a k e n i n a s t a t e ) \begin{aligned} value\ of\ action\ taken\ in\ a\ state &= Value\ of\ action\ taken\ in\ a\ state + \\ & learning\ rate\times (reward\ of\ moving\ to\ the\ next\ cell+\\ & \gamma\times Value\ of\ the\ best\ possible\ action\ in\ next\ state-\\ & Value\ of\ action\ taken\ in\ a\ state) \end{aligned} value of action taken in a state=Value of action taken in a state+learning rate×(reward of moving to the next cell+γ×Value of the best possible action in next state−Value of action taken in a state)

4.2 使用 Q 学习进行 frozen lake 游戏

目前强化学习 (Reinforcement learning, RL) 是三类方式的组合，包括试错、动态规划和蒙特卡罗模拟。基于此，Chris Watkins 在 1996 年提出了 Q-learning，Q-learning 已经成为 RL 的基础，并经常作为 RL 中的 Hello world。Q-learning 通过赋予智能体量化已知状态下给定动作的质量的能力来工作。通过测量给定动作的质量，智能体可以轻松地选择解决给定问题的正确动作序列。智能体仍然需要试错摸索，以推导动作或状态的质量。

4.3. frozen lake 问题

我们首先构建一个 Q-learning 智能体，解决 OpenAI Gym 中的基本问题------frozen lake 问题。OpenAI Gym 是一个开源项目，封装了数百个不同的问题环境，范围从经典Atari游戏到基本控制问题。

为 Q-learning 智能体构建的 frozen lake 环境如下所示，该环境是一个 4x4 的方格网格，表示一个冻结的湖，湖的一些区域被冰固定并且可以安全地穿过，而其他区域不稳定，并有洞会导致智能体跌落并死亡，以此完成智能体回合。

frozen lake 问题的目标是智能体通过上下左右的操作来穿越网格。当智能体到达右下角时，表示回合完成并获得奖励，如果智能体掉进湖中的一个洞，同样表示回合结束，智能体得到负奖励。使用 OpenAI Gym 使得构建 RL 智能体和环境进行测试变得更加容易。

接下来，使用 Gym 创建环境。可以选择数百种不同的环境，只需将名称传递给 gym.make() 函数即可创建一个环境。然后，我们查询环境以获取动作和状态空间的大小，表示可用的离散值数量，frozen lake 环境中行动和状态空间都使用离散值。而在其它一些环境中，我们可能使用连续值表示动作和状态空间：

python 复制代码

import numpy as np
import gym
import random

env = gym.make("FrozenLake-v1", render_mode="rgb_array")
action_size = env.action_space.n
state_size = env.observation_space.n
print(action_size, state_size)

4.4 实现 Q 学习

(1) 在 Q 学习中，智能体将其知识或学习情况封装在 Q 表中，该表的维度、列和行由状态和可用动作定义。创建此表以表示智能体的知识，使用 np.zeros 构建此表，以创建 action_size 和 state_size 值大小的数组，结果是一个值数组，其中每一行表示状态，每个行上的列表示该状态下的动作质量：

python 复制代码

Q = np.zeros((state_size, action_size))
print(Q)

(2) 定义超参数，智能体穿过湖泊的每次旅程都被定义为一回合。total_episodes 超参数设置智能体将采取的总回合数，max_steps 值定义智能体在单个回合中可以采取的最大步数，学习率类似于深度学习中的学习率，gamma 是一个折扣因子，控制未来奖励对智能体的重要性，最后的超参数组控制智能体的探索：

python 复制代码

total_episodes = 50000       # Total episodes
learning_rate = 0.7          # Learning rate
max_steps = 99               # Max steps per episode
gamma = 0.95                 # Discounting rate

# Exploration parameters
epsilon = 1.0                 # Exploration rate
max_epsilon = 1.0             # Exploration probability at start
min_epsilon = 0.01            # Minimum exploration probability 
decay_rate = 0.005            # Exponential decay rate for exploration prob

Q 学习中的一个关键点是探索和利用之间的权衡，当智能体开始训练时，能够利用的知识很低，在 Q 表中所有元素都为零，这种情况下，智能体通常依赖于随机选择动作。随着知识的增加，智能体可以使用 Q 表中的值确定下一个最佳动作，但如果智能体的知识不完整，始终选择最佳动作可能会无法得到解决方案。因此，引入超参数 epsilon 控制智能体探索的概率。

(3) 定义 choose_action() 函数来权衡探索和利用。在函数中，生成一个随机均匀值并与 epsilon 进行比较，如果该值小于 epsilon，则智能体从动作空间中随机选择一个动作并返回，否则，智能体选择当前状态的最大质量动作并返回。随着智能体在环境中进行训练，epsilon 值将随时间减小，以表示智能体对探索的需求减少：

python 复制代码

def choose_action(state):
    if random.uniform(0, 1) > epsilon:
        return np.argmax(Q[state,:])  
    else:
        return env.action_space.sample()

(4) 智能体通过 Q 函数计算的知识累积来学习。Q 函数中的项表示当前的 Q 值、奖励和折扣因子 gamma，这种学习方法封装在 learn 函数中，该函数应用 Q 函数：

python 复制代码

def learn(reward, state, action, new_state):
    # Update Q(s,a):= Q(s,a) + lr [R(s,a) + gamma * max Q(s',a') - Q(s,a)]
    # qtable[new_state,:] : all the actions we can take from new state
    Q[state, action] = Q[state, action] + learning_rate * (reward + gamma * np.max(Q[new_state, :]) - Q[state, action])

(5) 训练智能体的代码分为两个循环，第一个循环遍历回合数，第二个循环遍历每一步。在每一步中，智能体使用 choose_action 函数选择下一个动作，然后通过调用 env.step(action) 执行动作。调用 step 函数的输出用于通过调用 learn 函数更新智能体在 Q 表中的知识。然后，检查确认回合是否完成以及智能体是否掉进了洞或到达了终点。随着智能体在回合上循环，epsilon 值会减小，表示智能体随着时间的推移减少了探索的需要：

python 复制代码

rewards = []
epsilon = 1.0

# 2 For life or until learning is stopped
for episode in range(total_episodes):
    # Reset the environment
    state = env.reset()
    state = state[0]
    step = 0
    done = False
    total_rewards = 0
    
    for step in range(max_steps):  
        action = choose_action(state)    

        #excute the action
        new_state, reward, done, info, _ = env.step(action)

        learn(reward, state, action, new_state)
        
        total_rewards += reward        
        # Our new state is state
        state = new_state
        
        # If done (if we're dead) : finish episode
        if done == True: 
            break

    # Reduce epsilon (because we need less and less exploration)
    epsilon = min_epsilon + (max_epsilon - min_epsilon)*np.exp(-decay_rate*episode) 
    rewards.append(total_rewards)
    

print ("Score over time: " +  str(sum(rewards)/total_episodes))
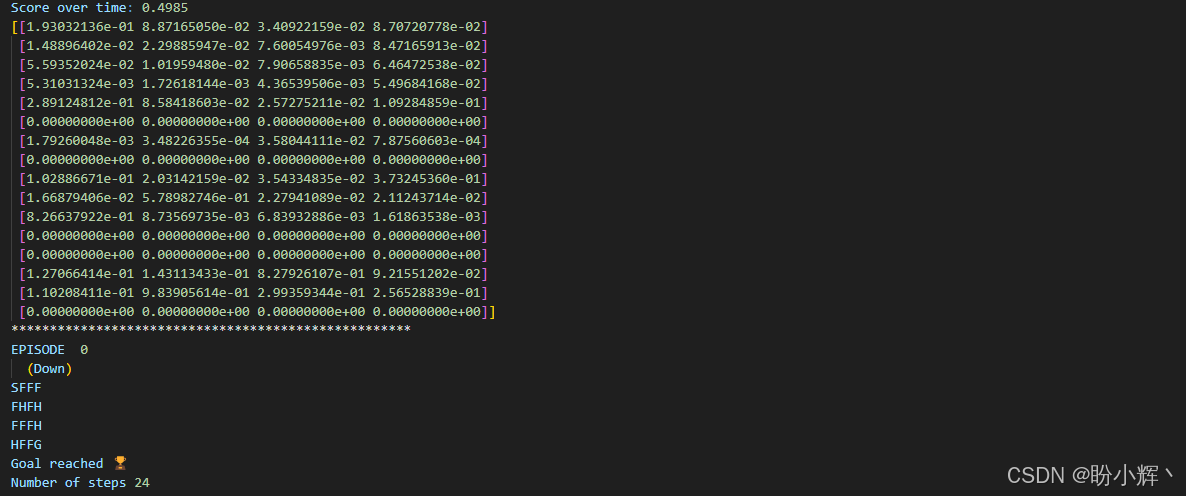
print(Q)

(6) 在本节中，我们训练智能体在一定数量的回合中运行，而不考虑性能的改进。智能体训练完成后，通过在环境中运行智能体进行模拟进行测试：

python 复制代码

env.reset()

for episode in range(5):
    state = env.reset()
    state = state[0]
    steps = 0
    done = False
    print("****************************************************")
    print("EPISODE ", episode)

    for step in range(max_steps):
        
        # Take the action (index) that have the maximum expected future reward given that state
        action = np.argmax(Q[state,:])
        
        new_state, reward, done, info, _ = env.step(action)
        
        if done:
            # Here, we decide to only print the last state (to see if our agent is on the goal or fall into an hole)
            env.render()
            if new_state == 15:
                print("Goal reached 🏆")
            else:
                print("Aaaah ☠️")
            
            # We print the number of step it took.
            print("Number of steps", step)
            
            break
        state = new_state
env.close()

在五个回合中运行经过训练的智能体的输出结果如下所示。从结果可以看出，智能体通常能够在最大允许的步数内解决环境。如果想回尝试改进智能体解决问题的速度，可以通过修改超参数，并重新运行。

小结

强化学习 (Reinforcement learning, RL) 的工作原理是让智能体观察环境的状态。对环境的观察或视图通常称为当前状态，智能体根据观察到的状态做出预测或动作。然后，基于该动作，环境根据给定状态提供奖励。它能够解决具有不确定性和复杂性的问题，并在动态环境下实现自主学习和决策能力。

系列链接

进化深度学习
 生命模拟及其应用
 生命模拟与进化论
 遗传算法（Genetic Algorithm）详解与实现
 遗传算法中常用遗传算子
 遗传算法框架DEAP
DEAP框架初体验
 使用遗传算法解决N皇后问题
 使用遗传算法解决旅行商问题
 使用遗传算法重建图像
 遗传编程详解与实现
 粒子群优化详解与实现
 协同进化详解与实现
 进化策略详解与实现
 差分进化详解与实现
 神经网络超参数优化
 使用随机搜索自动超参数优化
 使用网格搜索自动超参数优化
 使用粒子群优化自动超参数优化
 使用进化策略自动超参数优化
 使用差分搜索自动超参数优化
 使用Numpy构建神经网络
 利用遗传算法优化深度学习模型
 在Keras中应用神经进化优化
 使用Keras构建卷积神经网络
 编码卷积神经网络架构
 进化卷积神经网络
 卷积自编码器详解与实现
 编码卷积自编码器架构
 使用遗传算法优化自编码器模型
 变分自编码器详解与实现
 生成对抗网络详解与实现
 WGAN详解与实现
 编码WGAN
使用遗传算法优化生成对抗网络
 NEAT详解与实现
 NEAT初体验
 使用NEAT进行图像分类
 物种分化在进化拓扑中的作用