引言
在电学中,偶极子是一个非常重要且有趣的概念。它由两个电荷(一个正电荷和一个负电荷)组成,并且这两个电荷具有相同的大小和相反的符号。偶极子的电场分布具有独特的特点,能够帮助我们深入理解电场的性质。今天,我们将通过 Python 来可视化偶极子的电场,帮助大家更直观地理解这一物理现象。
什么是偶极子?
偶极子是由一对大小相等、符号相反的电荷组成的系统。常见的偶极子模型是两个电荷之间保持一定的距离,电荷大小相等,符号相反。偶极子的电场通常可以用来描述许多物理现象,例如分子间的相互作用。
偶极子电场的一个重要特征是:它在距离偶极子较远的地方表现出类似于单一电荷的电场,但随着距离的增大,偶极子的影响会逐渐减弱,并且电场的形状也会发生变化。
偶极子电场的公式
偶极子产生的电场可以通过以下公式来表示:$$\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi \epsilon_0} \left( \frac{1}{r^3} \right) \left[ 3(\mathbf{p} \cdot \hat{r})\hat{r} - \mathbf{p} \right]$$
其中:
- \(\mathbf{E}(\mathbf{r})\) 是在某个位置 \(\mathbf{r}\) 上的电场强度。
- \(\mathbf{p}\) 是偶极矩,表示偶极子的大小和方向,\(\mathbf{p} = q \cdot d\),其中 q 是电荷的大小,d 是电荷间的距离。
- \(\hat{r}\) 是从偶极子指向观察点的单位向量。
- \(\epsilon_0\) 是真空中的电常数。
- r 是从偶极子到观察点的距离。
通过这个公式,电场强度不仅与距离有关,还与偶极子的方向和电荷的排列方式密切相关。
使用 Python 绘制偶极子电场
接下来,我们将用 Python 进行偶极子电场的可视化。为了简化,我们将使用 matplotlib 来绘制电场线,并通过 numpy 进行数值计算。
安装所需库
首先,确保你安装了 matplotlib 和 numpy 这两个库。如果没有安装,可以通过以下命令进行安装:
pip install matplotlib numpy编写代码进行电场计算和可视化
# coding=utf-8
import matplotlib
matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt
# 定义常量
epsilon_0 = 8.85e-12 # 真空电常数,单位:C^2/(N·m^2)
q = 1e-9 # 电荷大小,单位:C
d = 1e-2 # 电荷间距,单位:m
# 计算偶极矩
p = q * d # 偶极矩
# 计算电场的函数
def electric_field(x, y):
# 计算距离原点的坐标
r = np.sqrt(x ** 2 + y ** 2)
if r == 0:
return np.array([0, 0]) # 避免除以零
# 计算电场
r_hat = np.array([x, y]) / r # 单位向量
r_cube = r ** 3
term1 = (3 * np.dot(p, r_hat) * r_hat) / r_cube
term2 = p / r_cube
E = (1 / (4 * np.pi * epsilon_0)) * (term1 - term2)
return E
# 创建网格
x_vals = np.linspace(-1, 1, 20) # x坐标范围
y_vals = np.linspace(-1, 1, 20) # y坐标范围
X, Y = np.meshgrid(x_vals, y_vals)
# 计算每个网格点的电场
Ex, Ey = np.zeros(X.shape), np.zeros(Y.shape)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
E = electric_field(X[i, j], Y[i, j])
Ex[i, j], Ey[i, j] = E[0], E[1]
# 绘制电场线
plt.figure(figsize=(6, 6))
plt.streamplot(X, Y, Ex, Ey, color='b', linewidth=1)
plt.title("Visualization of the electric field of a dipole")
plt.xlabel("X")
plt.ylabel("Y")
plt.grid(True)
plt.axis("equal")
plt.savefig('electric.png')代码解析
- 电场计算 :electric_field 函数计算了偶极子在某一点的电场强度。我们根据偶极子的电场公式进行计算,得到电场的分量 \(E_x\) 和 \(E_y\)。
- 网格生成:使用 np.meshgrid 创建一个网格,表示我们要在其中计算电场的空间区域。
- 电场计算与绘制:通过遍历网格上的每个点,计算电场并通过 plt.streamplot 绘制电场线。streamplot 会根据电场的方向和大小绘制电场线,帮助我们直观地观察电场的分布。
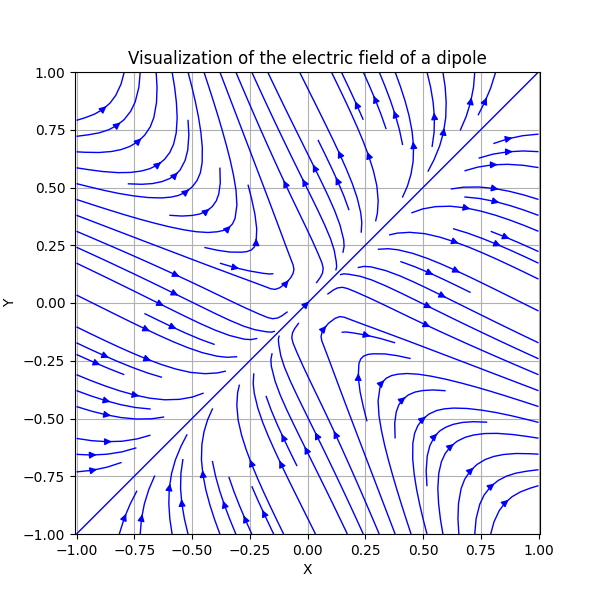
结果展示
运行上述代码后,你将看到一个图像,显示偶极子周围的电场线。你会发现,电场线在偶极子附近呈现出对称分布,并且朝向偶极子的正负电荷分布情况。通过可视化,我们能够更好地理解偶极子电场的结构和变化。
总结
通过这篇文章,我们不仅学到了偶极子的基本概念,还通过 Python 实现了偶极子电场的可视化。可视化让我们更加直观地理解了偶极子的电场分布,并且帮助我们加深了对电场力学的理解。希望这篇文章能够激发大家对电场、分子电磁学以及 Python 编程的兴趣,欢迎大家留言讨论并分享自己的想法!