多变量决策树：机器学习中的“多面手”

在机器学习的广阔领域中，决策树一直是一种备受青睐的算法。它以其直观、易于理解和解释的特点，广泛应用于分类和回归任务。

然而，随着数据复杂性的不断增加，传统决策树的局限性逐渐显现。

本文将深入探讨多变量决策树这一强大的工具，它不仅克服了传统决策树的瓶颈，还为处理复杂数据提供了新的思路。

1. 基本概念

1.1. 传统决策树的局限性

传统决策树通过单一分割特征来构建模型，在每个节点，它选择一个特征进行划分，将数据分为多个子集。

这种方法虽然简单直观，但在处理多变量数据时存在明显的瓶颈。

当数据中存在多个相关特征时，单一分割特征的方法可能无法充分利用这些特征之间的复杂关系，从而导致模型的预测精度受限。

比如，在金融风险评估、医疗诊断、图像识别等领域，数据中往往包含多个相关特征。

为了更好地捕捉这些特征之间的复杂关系，多变量决策树应运而生，它通过综合考虑多个变量来构建模型，能够更准确地反映数据的真实结构。

1.2. 多变量决策树结构

多变量决策树 是一种扩展的决策树算法，它在每个节点上考虑多个特征的组合，而不是单一特征。

在结构上，多变量决策树与传统决策树类似，由根节点、内部节点和叶节点组成，

不同之处在于，多变量决策树的每个节点可以同时考虑多个特征的组合来进行划分。

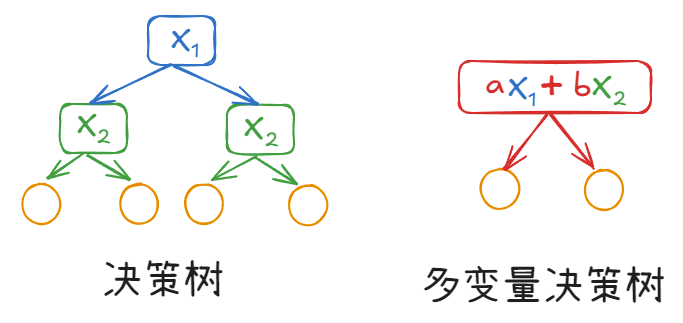
比如，在一个二元分类任务中，一个节点可能会根据特征 X_1 和 X_2 的线性组合 aX_1 + bX_2 \\(来进行划分，而不是单独考虑\\) X_1 \\(或者\\) X_2 。

此外，多变量决策树模型的训练步骤和决策树一样，也是：

1. 特征选择：通常通过优化一个目标函数（如信息增益、基尼不纯度等）来确定最优的特征组合
2. 节点划分：在节点划分时，考虑多个特征的组合
3. 树的剪枝：为了避免过拟合，剪枝技术（如预剪枝和后剪枝）也被广泛应用

2. 主要作用和优势

多变量决策树的作用和优势主要包括：

2.1. 处理复杂数据关系

多变量决策树能够更好地处理数据中多个特征之间的复杂关系。

在实际应用中，数据中的特征往往不是独立的，而是相互关联的。

例如，在金融风险评估中，客户的收入、信用记录和消费习惯等多个因素共同影响其违约风险，多变量决策树通过综合考虑这些因素，能够更准确地预测违约风险。

2.2. 提高模型可预测性

通过捕捉多个特征之间的复杂关系，多变量决策树能够显著提高模型的预测能力。

在处理多变量数据时，多变量决策树的预测准确率通常高于传统决策树。

例如，在一个医疗诊断任务中，多变量决策树能够更准确地预测疾病的发生概率。

2.3. 可解释性强

多变量决策树保留了传统决策树的可解释性，它的树结构清晰地展示了决策过程，使用户能够理解模型的决策依据。

例如，在医疗诊断中，医生可以通过多变量决策树的结构，了解哪些因素对疾病的诊断起到了关键作用，从而更好地与患者沟通。

2.4. 灵活性，高效性和鲁棒性

多变量决策树在处理不同类型数据（如连续型、离散型、混合型数据）时表现出良好的灵活性。

它能够适应各种复杂的数据环境，同时在训练和预测过程中保持较高的效率。

此外，多变量决策树对噪声数据和异常值具有较强的鲁棒性，能够更好地应对数据质量问题。

3. 使用示例

scikit-learn库中没有直接支持多变量决策树 ，但是可以基于scikit-learn来实现类似的功能。

下面基于scikit-learn库简单实现了一个多变量决策树 模型（MultivariateDecisionTree）。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score


class MultivariateDecisionTree:
    def __init__(self, max_depth=5):
        self.max_depth = max_depth

    def fit(self, X, y):
        self.tree = self._grow_tree(X, y, depth=0)

    def _grow_tree(self, X, y, depth):
        n_samples, n_features = X.shape
        n_labels = len(np.unique(y))

        # 停止条件
        if depth == self.max_depth or n_labels == 1:
            return np.bincount(y).argmax()

        best_gain = -1
        best_split = None
        for _ in range(10):  # 随机尝试一些线性组合
            weights = np.random.randn(n_features)
            thresholds = np.linspace(np.min(np.dot(X, weights)), np.max(np.dot(X, weights)), 10)
            for threshold in thresholds:
                left_indices = np.dot(X, weights) < threshold
                right_indices = ~left_indices
                if len(left_indices) == 0 or len(right_indices) == 0:
                    continue
                gain = self._information_gain(y, y[left_indices], y[right_indices])
                if gain > best_gain:
                    best_gain = gain
                    best_split = (weights, threshold)

        if best_gain == -1:
            return np.bincount(y).argmax()

        weights, threshold = best_split
        left_indices = np.dot(X, weights) < threshold
        right_indices = ~left_indices
        left_subtree = self._grow_tree(X[left_indices], y[left_indices], depth + 1)
        right_subtree = self._grow_tree(X[right_indices], y[right_indices], depth + 1)

        return (weights, threshold, left_subtree, right_subtree)

    def _information_gain(self, parent, left, right):
        p = len(left) / len(parent)
        return self._gini_impurity(parent) - p * self._gini_impurity(left) - (1 - p) * self._gini_impurity(right)

    def _gini_impurity(self, y):
        classes, counts = np.unique(y, return_counts=True)
        impurity = 1
        for count in counts:
            probability = count / len(y)
            impurity -= probability ** 2
        return impurity

    def predict(self, X):
        return np.array([self._traverse_tree(x, self.tree) for x in X])

    def _traverse_tree(self, x, node):
        if isinstance(node, (int, np.integer)):
            return node
        weights, threshold, left_subtree, right_subtree = node
        if np.dot(x, weights) < threshold:
            return self._traverse_tree(x, left_subtree)
        else:
            return self._traverse_tree(x, right_subtree)

然后使用MultivariateDecisionTree来对比传统的决策树模型。

测试数据生成一些关联性比较强的数据，也就是更适合MultivariateDecisionTree模型来处理的数据。

# 生成一个具有特征交互的数据集
def generate_complex_dataset(n_samples=1000, n_features=20):
    X = np.random.randn(n_samples, n_features)
    # 定义更复杂的规则，涉及多个特征的非线性组合
    y = ((X[:, 0] * X[:, 1] + X[:, 2] * X[:, 3]) * np.cos(X[:, 4]) + np.sin(X[:, 5]) * X[:, 6]) > 0
    y = y.astype(int)
    return X, y


# 生成数据集
X, y = generate_complex_dataset()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 传统决策树模型
single_tree = DecisionTreeClassifier(random_state=42)
single_tree.fit(X_train, y_train)
single_tree_pred = single_tree.predict(X_test)
single_tree_accuracy = accuracy_score(y_test, single_tree_pred)

# 多变量决策树模型
multi_tree = MultivariateDecisionTree(max_depth=5)
multi_tree.fit(X_train, y_train)
multi_tree_pred = multi_tree.predict(X_test)
multi_tree_accuracy = accuracy_score(y_test, multi_tree_pred)

# 输出结果
print(f"传统决策树的准确率: {single_tree_accuracy:.4f}")
print(f"多变量决策树的准确率: {multi_tree_accuracy:.4f}")

## 运行结果：
'''
传统决策树的准确率: 0.5000
多变量决策树的准确率: 0.5950
'''

从运行结果来看，多变量决策树的准确率要好一些。

注意：上面代码中的测试数据是随机生成的，你尝试的时候可能准确率和上面的不一样。

4. 总结

总之，多变量决策树作为一种强大的机器学习工具，为处理复杂数据提供了新的思路。

它能够更好地处理复杂数据关系，提高模型的预测能力，同时保持良好的可解释性，在金融、医疗、工业等多个领域具有广泛的应用前景。

不过，需要注意 的是，尽管多变量决策树具有许多优势，但它也面临一些挑战。

首先，多变量决策树的计算复杂度较高，尤其是在处理高维数据时；

其次，模型的选择和调优需要更多的专业知识和经验；

此外，数据质量问题（如噪声、缺失值等）也会影响多变量决策树的性能。