Android 视图转换工具 Matrix

我们在使用 Android Canvas 绘制各种图案或者 bitmap 时，如果需要旋转或平移图案，可能会这样用：

kotlin 复制代码

canvas.save()
canvas.translate(xxx)
canvas.scale(xxx)
canvas.rotate(xxx)
canvas.restore()

用过的同学应该很熟悉这种写法，这是最常见的 Canvas 转换方式，而它本质上就是用 Matrix 来实现的。

Matrix 是什么

Matrix 本质上是一个 3x3 的矩阵

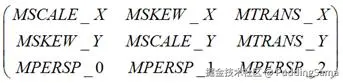
java 复制代码

    public static final int MSCALE_X = 0;   //!< use with getValues/setValues
    public static final int MSKEW_X  = 1;   //!< use with getValues/setValues
    public static final int MTRANS_X = 2;   //!< use with getValues/setValues
    public static final int MSKEW_Y  = 3;   //!< use with getValues/setValues
    public static final int MSCALE_Y = 4;   //!< use with getValues/setValues
    public static final int MTRANS_Y = 5;   //!< use with getValues/setValues
    public static final int MPERSP_0 = 6;   //!< use with getValues/setValues
    public static final int MPERSP_1 = 7;   //!< use with getValues/setValues
    public static final int MPERSP_2 = 8;   //!< use with getValues/setValues

根据这几个名称我们大概也能知道它们分别代表的功能：

缩放（Scale）
对应 MSCALE_X 与 MSCALE_Y
位移（Translate）
对应 MTRANS_X 与 MTRANS_Y
错切（Skew）
对应 MSKEW_X 与 MSKEW_Y
旋转（Rotate）
旋转没有专门的数值来计算，Matrix 会通过计算缩放与错切来处理旋转。

对应 Matrix 的方法分别是：

scss 复制代码

xxxScale()
xxxTranslate()
xxxSkew()
xxxRotate()

每种转换分别有 set、pre、post 三种变种，下面我们用一个demo演示下。

Matrix 简单应用

kotlin 复制代码

  override fun onDraw(canvas: Canvas) {
    super.onDraw(canvas)
    canvas.drawColor(Color.WHITE)
    canvas.drawBitmap(bitmap, matrix, paint)
  }

比如这段代码，绘制一个 bitmap，并传了一个默认的 Matrix，即没有任何转换的 Matrix，效果如下

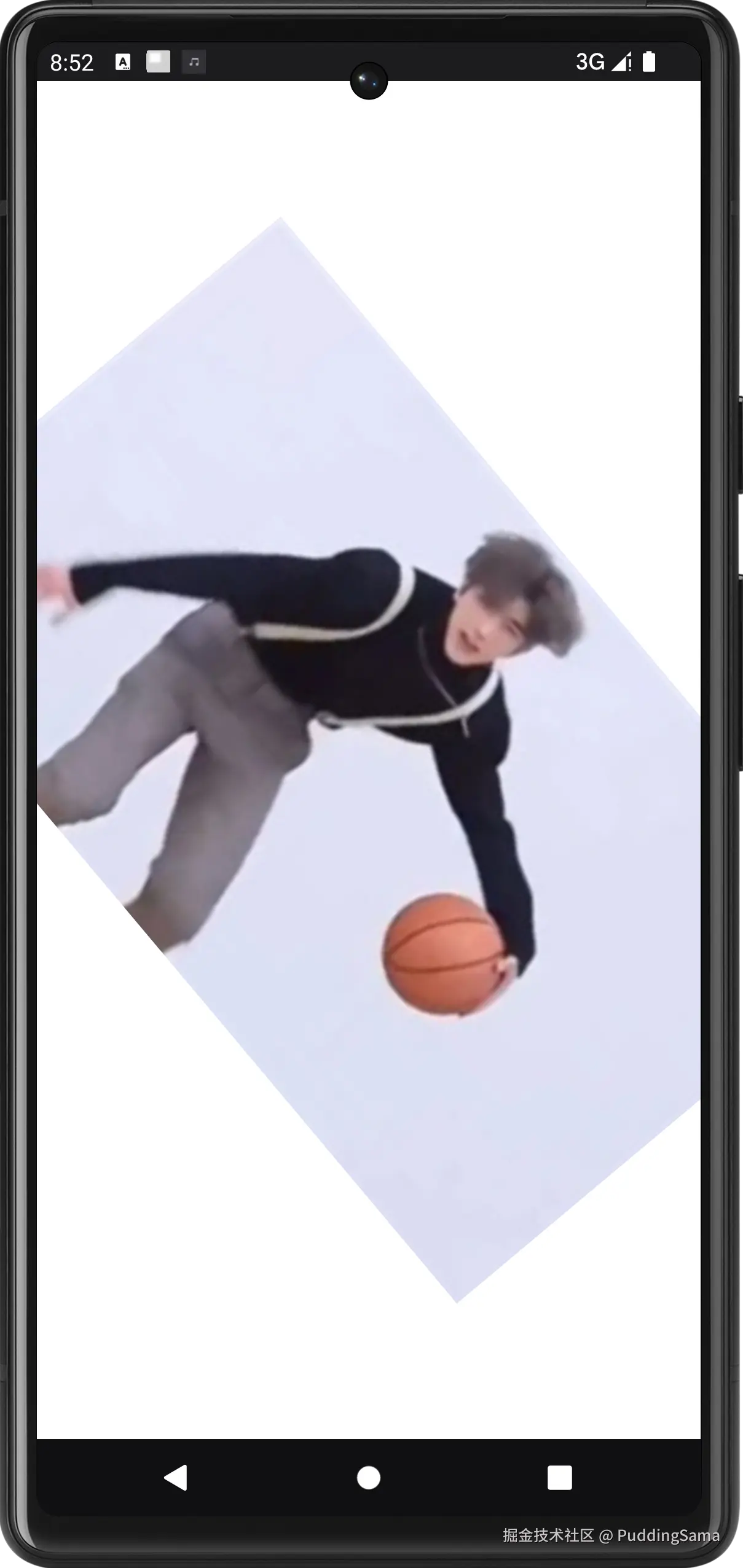
现在我们来实现一个效果，将图片居中、放大、旋转50度，看看如何实现，首先看代码：

kotlin 复制代码

override fun onDraw(canvas: Canvas) {
  super.onDraw(canvas)
  canvas.drawColor(Color.WHITE)
  matrix.postTranslate(width / 2f - bitmap.width / 2f, height / 2f - bitmap.height / 2f)
  matrix.postScale(2f, 2f, width / 2f, height / 2f)
  matrix.postRotate(50f, width / 2f, height / 2f)
  canvas.drawBitmap(bitmap, matrix, paint)
}

主要分三部：

将图片移动到屏幕中心点
从屏幕中心点放大2倍
沿中心点旋转 50 度

这几种转换是比较常见的，多数人应该都用过,Android View 也提供了相关的方法setTranslation、setScale、setRotation,大家应该都不陌生。细心的人可能会发现，我这边转化使用的方法都是 post开头，而 Matrix 提供了三种方式，分别是 set、post、pre，它们有什么区别，该怎么用呢？

Matrix set/post/pre 的区别

set

set 方法用于直接设置矩阵的值，它会丢弃矩阵之前的所有变换信息，将矩阵重置为新的变换矩阵。从线性代数的角度看，这相当于用一个新的矩阵完全替换原矩阵，而不涉及矩阵乘法。

kotlin 复制代码

matrix.postTranslate(width / 2f - bitmap.width / 2f, height / 2f - bitmap.height / 2f)
matrix.postScale(2f, 2f, width / 2f, height / 2f)
matrix.setTranslate(100f,100f)
matrix.postRotate(50f, width / 2f, height / 2f)

比如这段代码，实际生效的只有3、4行，set 之前的操作都会被覆盖。

post

post 方法用于在已有变换之后添加新的变换。从线性代数的角度看，这相当于将新的变换矩阵后乘到原矩阵上。假设原矩阵为 A，新的变换矩阵为 B，那么最终的变换矩阵 C=A×B。

kotlin 复制代码

matrix.postTranslate(width / 2f - bitmap.width / 2f, height / 2f - bitmap.height / 2f)
matrix.postScale(2f, 2f, width / 2f, height / 2f)

比如这段代码的执行顺序，会先执行 translate 然后执行 scale。

pre

pre 方法用于在已有变换之前添加新的变换。从线性代数的角度看，这相当于将新的变换矩阵前乘到原矩阵上。假设原矩阵为 A，新的变换矩阵为 B，那么最终的变换矩阵 C = B x A。

kotlin 复制代码

matrix.preTranslate(width / 2f - bitmap.width / 2f, height / 2f - bitmap.height / 2f)
matrix.postScale(2f, 2f, width / 2f, height / 2f)

比如这段代码，会先执行 scale 再执行 translate。

其实 pre 与 post 的差异就是矩阵乘法顺序的问题。区别于普通乘法AxB=BxA，矩阵的乘法是不支持这种交换定律的。所以它们执行的顺序不同会导致结果的不同。

关于矩阵算法大家可从其他途径了解，不了解其实也不影响对这些 API 的理解，只需要知道它们之间的差异就行。

总结：如果需要复合变换，在多数情况建议都使用post,原因很简单，就是这种方式比较符合思维习惯，其转换顺序是按照代码顺序一步一步地处理。而 pre 是倒着执行，不容易思考，更不推荐pre与post混用，会很容易被绕晕。

3D 转换

前面我们介绍了 Matrix 的 translate、scale、rotate 方法，这些一般是用来做平面转换。而 skew 方法--斜切，一般用来做 3D 转换，不过这个方法提供的是转换的原子能力，不是我们正常理解的转换。如：沿某个zhou旋转多少度，skew 是不能直接做到的。在 Android 里做 3D 转换一般使用 Camera，注意这个Camera可不是android.hardwar.Camera 而是 android.graphics.Camera，camera 提供了更符合现实习惯的 API。

比如,之前绘制的图片，如果要沿底边旋转50度，可以这样处理

kotlin 复制代码

override fun onDraw(canvas: Canvas) {
    canvas.drawRect(0f, 0f, bitmap.width.toFloat(), bitmap.height.toFloat(), paint)
    camera.rotateX(50f)
    camera.getMatrix(matrix)
    matrix.preTranslate(-bitmap.width / 2f, -bitmap.height.toFloat())
    matrix.postTranslate(bitmap.width / 2f, bitmap.height.toFloat())
    canvas.drawBitmap(bitmap, matrix, paint)
  }

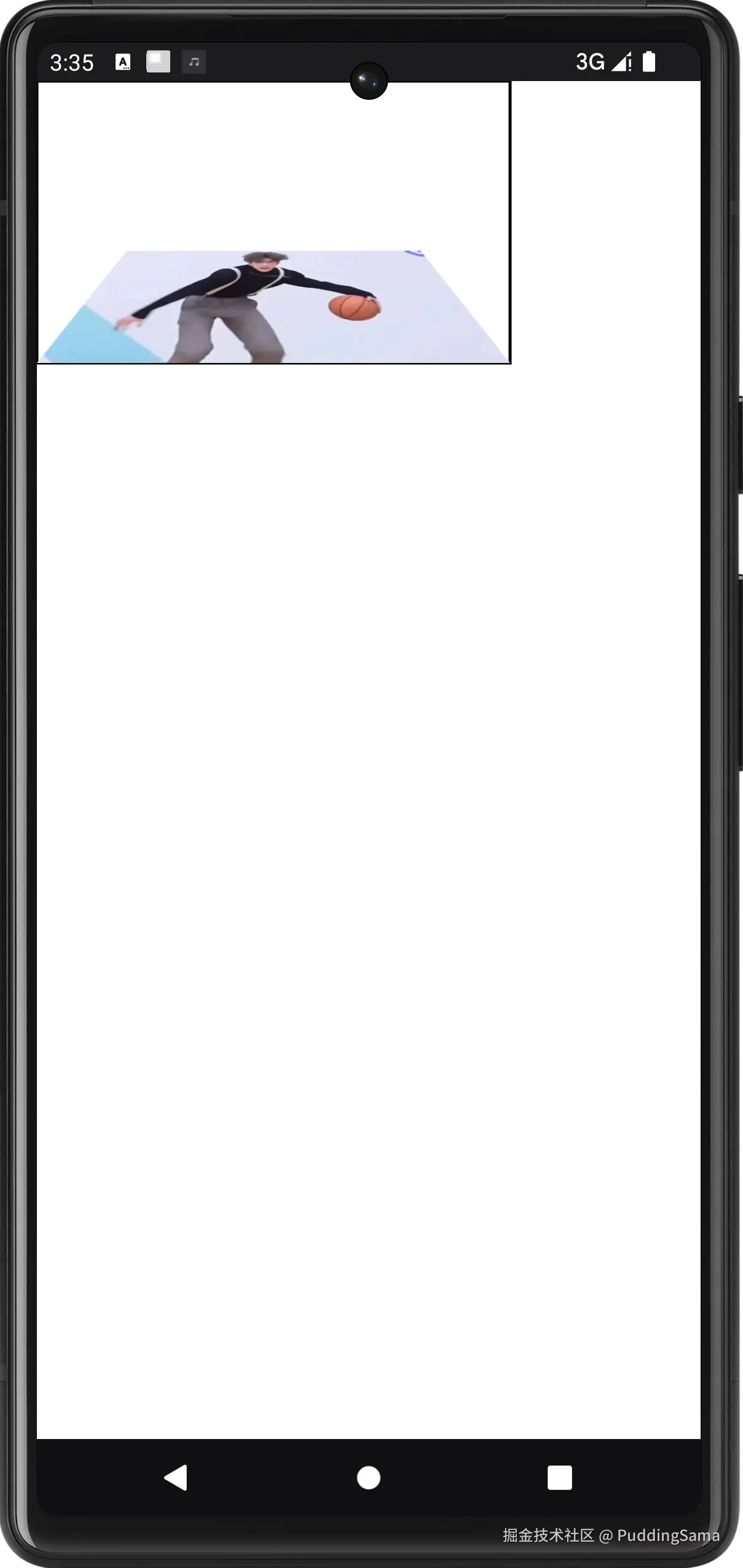
代码比较简单，camera.rotateX(50f)是沿X轴旋转 50°

arduino 复制代码

matrix.preTranslate(-bitmap.width / 2f, -bitmap.height.toFloat())
matrix.postTranslate(bitmap.width / 2f, bitmap.height.toFloat())

这两行是移动画布的位置。诶，之前不是说尽量不要pre``post混用吗，怎么这边就这样用了。这其实是 Camera 旋转的一个固定用法，比较简单。原因是 Camera的位置是在原点的 Z 轴，所以在旋转之前需要先将需要旋转的位置移动到 Camera 的正面位置，旋转之后再还原。我们用图来简单描述下：

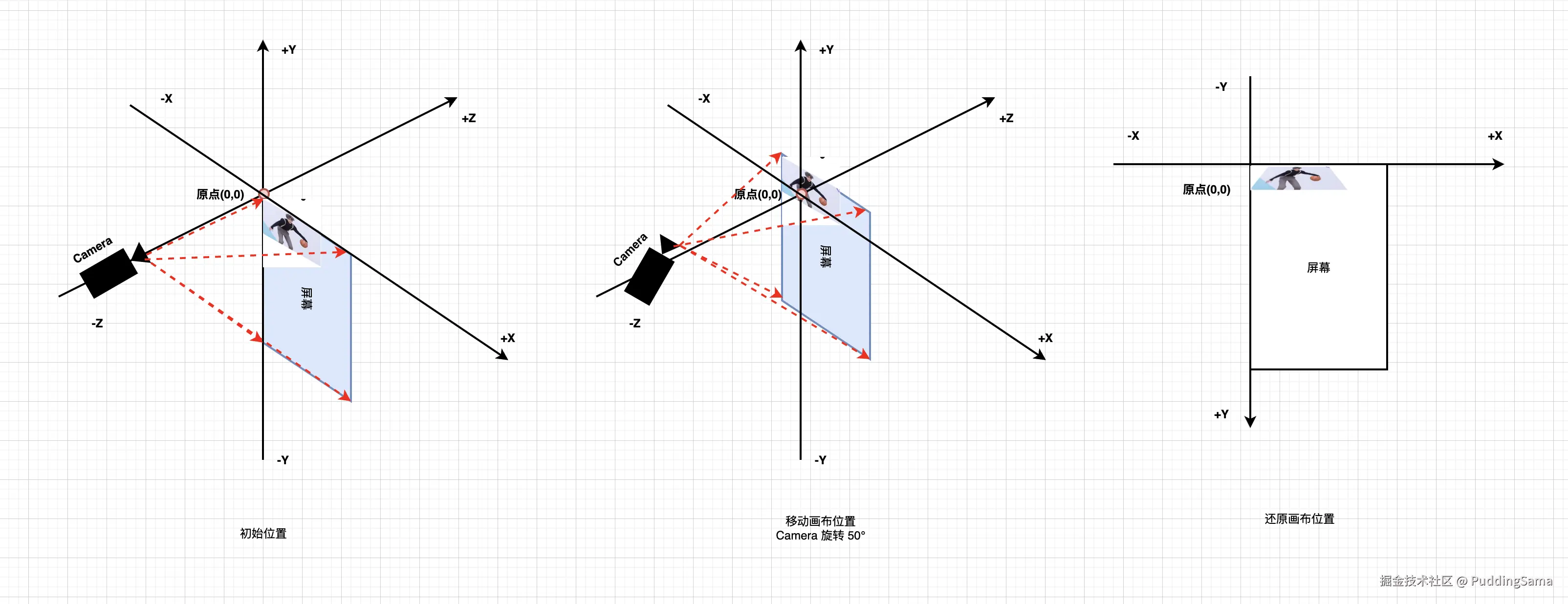
根据这个图示应该就比较明了上面代码的运行逻辑了吧。

其他常用方法

转换点

kotlin 复制代码

/**
 * Apply this matrix to the array of 2D points, and write the transformed points back into the
 * array
 *
 * @param pts The array [x0, y0, x1, y1, ...] of points to transform.
 */
public void mapPoints(float[] pts) {
    mapPoints(pts, 0, pts, 0, pts.length >> 1);
}

转换 Rect

（一般用来处理位移和缩放，因为 Rect 描述的始终是一个正矩形。所以如果 Matrix 中有旋转，最终还是会得到一个标准 Rect）

kotlin 复制代码

/**
 * Apply this matrix to the src rectangle, and write the transformed rectangle into dst. This is
 * accomplished by transforming the 4 corners of src, and then setting dst to the bounds of
 * those points.
 *
 * @param dst Where the transformed rectangle is written.
 * @param src The original rectangle to be transformed.
 * @return the result of calling rectStaysRect()
 */
public boolean mapRect(RectF dst, RectF src) {
    if (dst == null || src == null) {
        throw new NullPointerException();
    }
    return nMapRect(native_instance, dst, src);
}

这两个方法应用场景都比较广，通常应用场景出现在处理缩放上。比如，需要将相机的画面等比例缩放到屏幕上，因为相机的分辨率与屏幕不同，所以就需要缩放，这时候就可以用到

逆矩阵

kotlin 复制代码

/**
 * If this matrix can be inverted, return true and if inverse is not null, set inverse to be the
 * inverse of this matrix. If this matrix cannot be inverted, ignore inverse and return false.
 */
public boolean invert(Matrix inverse) {
    return nInvert(native_instance, inverse.native_instance);
}

逆矩阵顾名思义，则是会得到一个相反的矩阵，在需要处理一些还原转换时会比较常用。

结尾

到这里关于 Matrix 常用的内容就讲完了，希望对大家有用，有疑问也可以在评论区讨论。