[Python] 递推(讲解 + 刷题)

递推目录

递推理解
刷题部分

递推理解

递推是一种算法 --或者说解题思路 , 是靠找到后项(即将要求 的)与前项(已经求出 的或者初始的 )之间的关系, 从而把旧的后项变成新的前项, 继续求新的后项 的方法, 适用于一切有规律的数列.

刷题部分

1.斐波那契数列

题目描述

给出数列1, 1, 2, 3, 5, 8, ...，可以看出从第三个数开始，每一个数都是前两个数的和 ，这样的数列叫斐波那契数列，请问第n个数是多少？

输入输出描述

input:

一个正整数n

output:

输出斐波那契数列的第n个数

AC代码

python 复制代码

n = int(input())
# 生成全1列表, 大小n + 1
ls = [1 for i in range(n + 1)]  

# 从第3个数开始, 重复算到第n个数
for i in range(3, n): 
    # 根据递推关系, 计算当前数字
    ls[i] = ls[i - 1] + ls[i - 2]
    
print(ls[n])

2.跳格子

题目描述

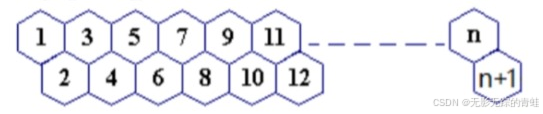
如图有编号为1到n+1的格子地图，跳格子游戏规则限制，只能从数字小的格子跳到数字大的相邻格子，请问在如图所示的格子地图中，从给定起点a和终点b，从a跳到b有多少种方案？

输入描述

输入两个正整数a，b，表示起点和终点位置(a < b)。

输出描述

输出一个正整数，表示从a跳到b有多少种方案。

样例输入输出

input:

复制代码

1 14

output:

复制代码

AC代码

python 复制代码

# 改装版斐波那契数列, 初始值是1和2
a, b = [int(i) for i in input().split()]
n = b - a
dp = [0 for i in range(1, n + 5)]
dp[1], dp[2] = 1, 2
for i in range(3, n + 1):
    dp[i] = dp[i - 1] + dp[i - 2]
print(dp[n])

3.病毒繁殖

题目描述

某种病毒具有很强的繁殖能力，从病毒粒子出生后的第5分钟开始，每分钟可以复制出一个新的病毒粒子 ，新出生的病毒粒子从第5分钟开始，也可以每分钟复制出一个新的病毒粒子。

举例来说，第1分钟时有一个病毒粒子，此病毒粒子从第5分钟开始复制新的病毒粒子，因此第5分钟时的病毒数量为2个；第6分钟时有复制出新的病毒粒子，因此第6分钟的病毒数量为3个；以此类推，第7分钟时病毒粒子数为4；第8分钟时病毒粒子数为5；第9分钟时，第5分钟复制出的病毒粒子开始复制新的病毒粒子，因此第9分钟时的病毒总数为7；第10分钟时，第6分钟复制出的病毒粒子开始复制新的病毒粒子，因此第10分钟时的病毒粒子总数为10.

计算病毒粒子总数，已知第一分钟时出生了一个病毒粒子，假设所有的病毒粒子不会自动死亡，请计算第N分钟时病毒粒子总数。

例如：前10分钟病毒粒子的总数分别为1, 1, 1, 1, 2, 3, 4, 5, 7, 10。

输入描述

输入正整数N（0<N≤30），表示时间

输出描述

输出第N分钟时，病毒粒子的总数

样例输入输出

input:

复制代码

output:

复制代码

AC代码

python 复制代码

n = int(input())
ls = [0 for i in range(n + 10)]
for i in range(1, 5):
	ls[i] = 1
	for i in range(4, n + 1):
		ls[i] = ls[i - 1] + ls[i - 4]
print(ls)