【25软考网工】第二章（8）差错控制、奇偶校验、CRC、海明码

|----------|---------------------------------------------|----------------------------|--------|
| 知识点 | 核心内容 | 考试重点/易混淆点 | 难度系数 |
| 差错控制基础 | 数据传输中错误不可避免，需采用差错控制方法。 | 差错控制的必要性。 | 🌟 |
| 差错控制方法 | 减错：接收方知道有错误，要求重传。纠错：接收方知道并纠正错误。 | 减错与纠错的区别与应用。 | 🌟🌟 |
| 差错控制核心原理 | 传k位数据，加入r位冗余，通过特定算法定义，接收方计算对比。 | 冗余加入与算法定义的理解。 | 🌟🌟🌟 |
| 减错与纠错的比较 | 减错应用更广，因为纠错开销大。 | 纠错的开销大，实际应用中减错重传更常用。 | 🌟🌟🌟 |
| 奇偶校验 | 常用的减错方法，能检出奇数位错，不能检出偶数位错。 | 奇偶校验的原理与限制。 | 🌟🌟 |
| 奇偶校验原理 | 在七位ASCII码后增加一位，形成八位，确保1的个数为奇数（奇校验）或偶数（偶校验）。 | 奇校验与偶校验的区别。 | 🌟🌟🌟 |
| 奇偶校验举例 | 奇校验：确保整个码字中1的个数为奇数；偶校验：确保1的个数为偶数。 | 如何根据数据计算校验位。 | 🌟🌟 |
| 奇偶校验练习题 | 选择题：关于一位奇校验的正确叙述是"若有奇数个数据位出错，可以检出来，但无法纠正"。 | 注意描述中的"所有奇数位"与"奇数个数据位"的区别。 | 🌟🌟🌟 |
| RAID 5应用 | 采用奇偶校验实现数据冗余保护，每个RAID组至少配三块硬盘。 | RAID 5的冗余实现方式与硬盘配置。 | 🌟🌟 |

二、差错控制------CRC循环冗余校验码

1. 循环冗余校验码计算

1）例题1

生成多项式:G(X)=X^4+X+1

信息码字: 10111

计算步骤:

判断校验位数: 生成多项式的最高次方是4，所以校验位是4位。
补齐数据位后面的0: 数据位后面补4个0，得到101110000。
提取生成多项式的系数:G(X)=1X^4+0X^3+0X^2+1X^1+1X^0= 10011
异或运算（模2余，即相同为0不同为1）: 用补齐后的数据位（第二步）除以生成多项式的系数（第三步），余数为CRC校验码，余数不够前面补0。

答案: D. 1100

2.循环冗余校验码总结

检错与纠错: CRC只能检错，不能纠错。只有海明码可以纠错

检错能力: 具有很强的检错能力，且容易用硬件实现，广泛用于局域网。

检测不到的概率: CRC有可能有差错而检测不到，概率约1/256。

生成多项式的特性:

若G(x)包含的项数大于1，则可以检测单个错。

若G(x)含有因子x+1，则可检测出所有奇数个错。

结论: 具有r个校验位的多项式能检测出所有长度小于等于r的突发性差错。
常用生成多项式:

CRC-CCITT:G(X)=X^16+X^12+X^5+1

CRC-16:G(X)=X^16+X^15+X^2+1

CRC-12：G(X)=G(X)=X^12+X^11+X^3+X^2+X+1

CRC-32:G(X)=X^32+X^26+X^23+X^22+X^16+X^12+X^10+X^3+X^2+X+1

其中 CRC-32多用于局域网中。

1）例题1

生成多项式:G(X) = X^16 + X^15+ X^2 + 1
校验码位数: 最高次方是16，所以校验码是16位。
接收端发现错误采取的措施: CRC只能检错，不能纠错，所以采取的措施是自动请求重发。
答案: C. 重新生成数据, D. 自动请求重发

2）例题2

生成多项式:X^5 + X^3 + 1
传输数据: 10101110
校验码位数: 最高次方是5，所以校验码是5位。
答案: A. 01000

3）例题3

生成多项式:G(x)=X^3+X^2+1
接收方收到的码字: 校验位是3位，接收方收到的码字最后三位是校验位。在数据位后补3个0，接收方接收到的码子后三位为检验位001，数据位为101101，补0后为101101 000
生成多项式的系数为1101
进行异或运算：101101 000除以1101
错误选项分析:
- A. 生成多项式各项系数提取正确。
- B. 收发双方应使用相同的生成多项式，正确。
- C. 校验位判断正确。
- D. 接收方认为收到的信息没有出现错误，错误。因为接收方需要计算CRC校验码010并与收到的校验码001比较，不一致则说明出现错误。
答案: D. 接收方认为收到的信息是没有出现错误的。

知识小结

|-----------------|----------------------------------------------------------------------------------------------------------|---------------------------|----------|
| 知识点 | 核心内容 | 考试重点/易混淆点 | 难度系数 |
| CRC（循环冗余校验）基本概念 | CRC是差错控制中的一种方法，用于校验数据传输过程中的错误。 | CRC的定义和作用。 | 🌟 |
| CRC计算步骤 | 1. 判断校验位位数（与生成多项式最高次方相关）。 2. 补全数据位后面的零（与校验位位数相同）。 3. 提取生成多项式的系数。 4. 用第二步的结果除以第三步的结果，进行异或运算，得到余数即为CRC校验码。 | 每一步的具体操作和注意事项，特别是异或运算的理解。 | 🌟🌟🌟 |
| CRC校验码的应用 | 在数据末尾加入CRC校验码，接收方通过相同生成多项式计算CRC，对比发送方的CRC校验码以检测错误。 | CRC校验码在数据传输中的作用和如何使用。 | 🌟 |
| CRC的特性与局限性 | 具有很强的检错能力，但不能纠错。容易用硬件实现，广泛应用于局域网。可能存在检测不到的错误，概率约为二百五十六分之一。 | CRC的检错能力、应用场景和检测不到的错误概率。 | 🌟🌟 |
| 生成多项式的特性 | 生成多项式不是随便的，需要有一定特性才能检测出各种错误。项数大于一可以检测出单个错。有x+1因子可以检测出所有奇数个错。 | 生成多项式的特性和作用。 | 🌟🌟🌟 |
| 校验位与生成多项式的关系 | 校验位的位数与生成多项式的最高次方相关，决定了CRC校验码的长度和检错能力。 | 校验位和生成多项式最高次方的关系。 | 🌟🌟 |
| CRC练习题解析 | 通过具体题目展示CRC计算过程，包括判断校验位位数、补零、提取系数、进行异或运算等步骤。 | 练习题中的关键步骤和易错点。 | 🌟🌟🌟🌟 |

三、差错控制------海明码

1. 海明码的概念

海明码: 通过冗余数据位来检测和纠正差错的编码方式。
特点: 海明码能够纠正错误，而其他如奇偶校验、CRC等只能检错，不能纠错。

1）海明距离

海明距离（码距）: 一个码字要变成另一个码字时必须改变的最小位数，即两个码字之间不同的比特数。

例题说明

例子: 假设有两个码字"10101 00"和"10110 11"，它们之间只有最后两位不同，因此它们的海明距离是2。但如果比较"10101"和"00110"，则有三位不同，海明距离就是3。

2）题型(通信工程师2022年10月第28题)

题目解析

审题过程: 题目要求计算两个码字"10101"和"00110"的码距，即找出它们之间不同二进制码元的个数。
解题思路: 逐位比较两个码字，统计不同位的数量。
选项分析: A.1 B.2 C.3 D.4，通过比较可知，两个码字有三位不同。
答案: C（3）
考点: 海明距离的计算方法，即两个码字之间不同二进制码元的个数。
易错点: 可能误将海明距离与码字的长度或其他概念混淆。

2. 海明码的原理与海明不等式

1）海明码的原理

定义: 在数据中间加入几个校验码，让码距均匀拉大。

特点: 当某一位出错时，会引起几个校验位的值发生变化，从而可以判断出具体哪一个数据位出了问题。

对比CRC: CRC校验码是在数据末尾添加，而海明码是在数据中间添加校验码。

2）海明不等式（重点）

校验位与信息位关系: 校验码个数为k，可以表示2^k个信息，其中1个信息用来表示"没有错误"，剩余的2^k - 1个信息用来表示数据中存在的错误。

不等式内容: 如果满足2^k−1⩾m+k（m为信息位，m+k为编码后的总长度），则在理论上k个校验码就可以判断是哪一位出现了问题。

重要性: 海明不等式是海明码能够检测出哪一位出错误的前提条件，即校验位个数k和信息位m要满足此不等式。

3. 海明码的编码方法

1）第2i位是校验位

海明码定义: 海明码是一种错误校正码，用于检测并纠正数据传输中的错误。
校验位位置: 在海明码中，第2^i（i=0,1,2,3...）位是校验位，其余位存放数据。例如，1,2,4,8位是校验位。
数据位位置: 除校验位外的其他位置用于存放数据，如3,5,6,7,9,10,11等位置。

2）例题

题目解析

首先，将传送信息1001011放在数据位上，即3,5,6,7,9,10,11位置。2^i即1、2、4、8保留作为校验位
接着，确定每个校验位。将每个数据位拆分成校验位相加（2的次方和）。例如，3,5,7,9,11位包含1，因此第一位校验位由3,5,7,9,11位的数据生成。
默认采用偶校验方式。若这些位中1的个数为奇数，则校验位填1；若为偶数，则填0。如第1位校验位由3,5,7,9,11位生成，10101有3个1，则第一位校验位为1。
类似地，求出其他校验位。如第2位校验位由3、6、7、10、11生成。10111，则第2位校验位为0。

错误检测与纠正:

假设传输中第六位出错，由0变为1。
接收端按照同样规则计算校验位时，会发现2和4号位的奇偶性不对。
由于2和4号位对应的数值是4和2，它们的和是6，因此可以立即确认错在6号位。
结果: 通过海明码的编码方法，我们可以有效地检测并纠正数据传输中的一位错误。

编码结果: 如图所示，最终得到的海明码为101100100111，其中1,2,4,8位为校验位，其余为数据位。
错误检测: 如果6号位出错，通过校验位的计算可以迅速定位并纠正错误。

4. 海明码纠错原理及应用

1）海明码基本概念

海明码定义: 海明码是一种纠错码，通过为数据位增加校验位，实现错误的检测和纠正。
海明距离: 一对有效码字之间的海明距离是指一个码字要变成另一个码字时必须改变的最小位数，即两个码字之间不同的比特数。

2）例题1

题目解析

审题过程: 题目要求计算信息位为6位时，为纠正1位错误至少需要增加的校验位数。
解题思路: 应用海明不等式2^k−1≥m+k，其中m为数据位，k为校验位。代入m=6，求解k的最小值。
计算过程:
- 当k=3时，2^3−1=7<6+3，不满足条件。
- 当k=4时，2^4−1=15≥6+4，满足条件。
答案: 至少需要增加4位校验位，选项B正确。
考点: 海明不等式的应用。

3）例题2

2^k−1≥m+k，其中m为数据位，k为校验位。代入m=32，求解k的最小值。最后得到K=6符合要求。选D
P1、P2、P3、P4对应为1、2、4、8校验位。
依次从右向左编号0、1、2^13、14，D5编号为10=8+2对应为P4、P2.选B

4）例题3

题目解析

审题过程: 题目要求计算信息位长度为7时，为纠正单个错误至少需要添加的校验位数。
解题思路: 同样应用海明不等式，代入m=7，求解k的最小值。
计算过程:
- 通过尝试或计算，得出k应大于等于4。
答案: 至少需要添加4位校验位，选项C正确。
考点: 海明不等式的应用及计算。

5）例题4

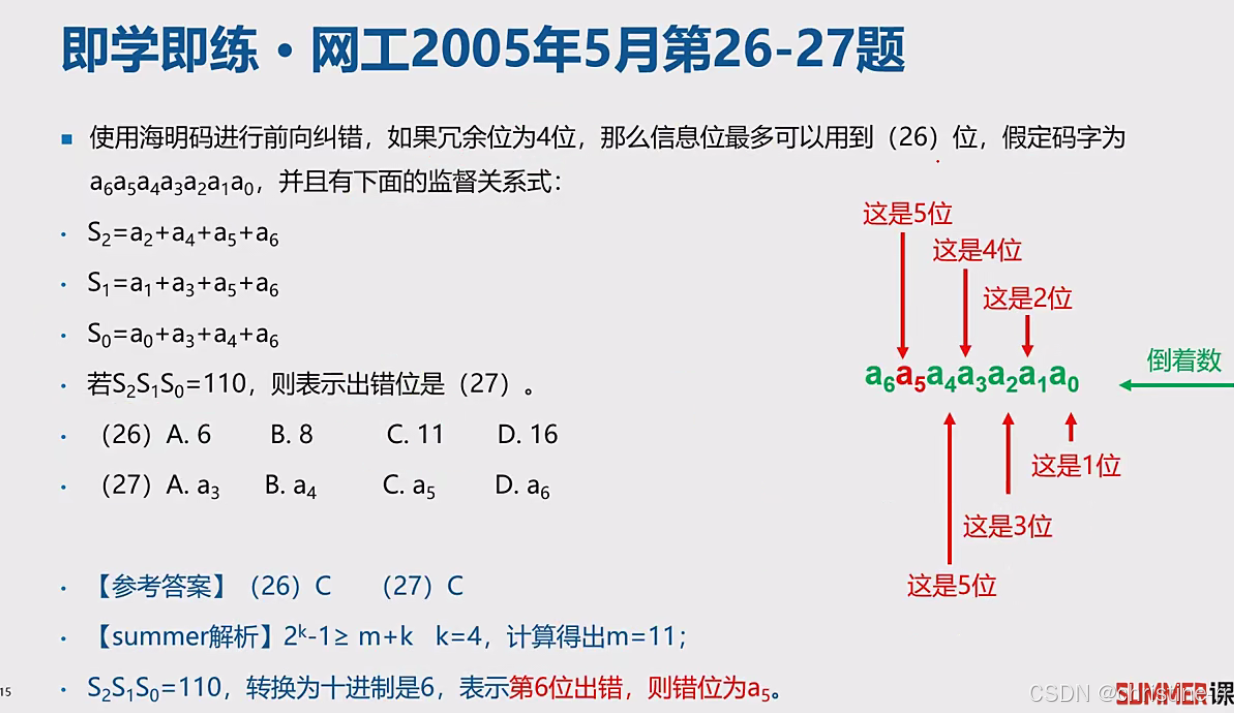
题目解析

审题过程: 题目给出冗余位（校验位）为4位，要求计算信息位最多可以用到多少位。
解题思路: 应用海明不等式，但此次需求解的是信息位m的最大值。已知k=4，代入求解m。
计算过程:
- 2^4−1−4=11，因此信息位最多可以用到11位。
答案: 信息位最多可以用到11位，选项C正确。
S1S2S3=110，转换为二进制位6，表示第六位出错，为a5,选项C正确。
考点: 海明不等式的变形应用及计算。

6）例题5

题目解析

审题过程: 题目给出7位码片，其中4位数据位，3位校验位，以及监督关系式，要求根据收到的错误码字进行纠错。
解题思路:
- 首先将收到的码字与7位码片对应，注意倒序对应。
- 然后根据监督关系式计算校验位的值，并转换为十进制数定位错误位。
计算过程:
- 收到的码字1000101对应X7X6X5X4X3X2X1X，监督关系式计算得C2C1C0=101，转换为十进制数为5，表示倒向第5位出错。
- 纠正后码字为1010101。
答案: 纠错后的码字是1010101，选项C正确。
考点: 海明码的错误定位与纠正方法。
注意: 此题涉及偶校验的理解和应用，以及十进制与二进制的转换。

方法二（正向算）

知识小结

|---------|-----------------------------------------|-----------------|--------|
| 知识点 | 核心内容 | 考试重点/易混淆点 | 难度系数 |
| 海明码 | 通过融余数据位来检测和纠正错误的编码 | 海明码的概念和原理 | ⭐⭐⭐⭐⭐ |
| 海明距离/码距 | 两个码字之间不同的比特数 | 海明距离的计算和含义 | ⭐⭐ |
| 海明不等式 | 2^k - 1 >= m + k，其中k是校验位，m是信息位 | 不等式的理解和应用，是考试重点 | ⭐⭐⭐⭐⭐ |
| 海明码编码方法 | 在数据中间加入校验码，让码距均匀拉大，通过校验位的变化判断错误位置 | 编码方法复杂，是难点 | ⭐⭐⭐⭐⭐⭐ |
| 海明码纠错原理 | 当某一位出现错误时，会引起几个校验位的值发生变化，根据变化的校验位判断错误位置 | 纠错原理的理解 | ⭐⭐⭐⭐ |
| 海明码练习题 | 包括海明距离的计算、海明不等式的应用、海明码编码和纠错等 | 练习题的解答和技巧 | ⭐⭐⭐ |
| 海明码效率 | 海明码虽然能纠错，但效率不高，校验码占比较大 | 海明码的优缺点评价 | ⭐⭐ |