重新开始学Threejs，了解一下里面的一些高级几何体

有段时间没有看Threejs了，上次看这部分内容还是在上家公司，后来经历了裁员，然后两个月的找工作，接着再适应新工作再到现在，已经过了大半年了，弄的自己把刚学没多久的一些皮毛也忘了个一干二净，没办法只能从头开始在学一遍，刚开始还是蛮顺利的，毕竟以前学过一遍，这次简单看看，敲敲代码就能想起来个大概，但是在看几何体的时候发现，几何体居然还分什么高级几何体，原本以为几何体就那几样东西，现在看来还是自己太年轻了，那么我们就来看看这些高级几何体究竟高级在哪

ConvexGeometry

这个几何体叫凸包几何体，也就是专门用来创建凸包的，可能有人第一次听说凸包这个名词，这里解释下，我们可以想象空间当中存在若干的点，而能够把这些点完全包围住的几何体我们就称之为凸包，类似于我们路边看到的一块石头，任意石头都是有几处尖锐的棱角的，这些棱角就相当于是点，而这个石头就是包围这些点的凸包，所以我们想要创建一个凸包几何体的话，首先就要创建点

var points = []
for (let index = 0; index < 30; index++) {
    var randomx = -15+Math.round(Math.random()*30)
    var randomy = -10+Math.round(Math.random()*25)
    var randomz = -15+Math.round(Math.random()*25)
    points.push(new THREE.Vector3(randomx,randomy,randomz))
}

这里创建了一个顶点数组，数组里面随机放进去了30个顶点，有了这些顶点后下一步就是创建ConvexGeometry类，这里注意的是，Threejs的标准库里面是不包含ConvexGeometry的，需要额外导入文件才能使用

import { ConvexGeometry } from "three/examples/jsm/geometries/ConvexGeometry";
...
var convexGeo = new ConvexGeometry(points)

创建ConvexGeometry很方便，它的构造函数内只需要一个顶点数组即可，现在有了几何体，那么我们就要给它加上点皮肤，为了看的明显一些，这里使用MeshStandardMaterial材质创建一个带金属质感的皮肤

const vexmaterial = new THREE.MeshStandardMaterial({
    color: 0x9400d3,
    wireframe: false,
    roughness:0.5,
    metalness:0.5
});

最后将它添加到场景中，我们就能看到创建好了的凸包了

const convexMesh = new THREE.Mesh(convexGeo, vexmaterial);
scene.add(convexMesh);

这个几何体理解起来不困难，接下去看下一个

LatheGeometry

这个几何体用来创建一些轴对称图形，有人叫它是榫卯体，要创建一个榫卯体需要四个参数

export class LatheGeometry extends BufferGeometry {
    constructor(points?: Vector2[], segments?: number, phiStart?: number, phiLength?: number);
}

• points:一个Vector2的数组，是整个图形轮廓的点，其中x坐标必须大于0
• segments:分段数目，数值越高，图形就会越圆
• phiStart:创建图形是指定从圆的什么位置开始，取值范围是0～2*PI
• phiLength:表示图形的完整性，也可以理解为经过的弧度

首先先来创建一个Vector2的数组，数组的x,y坐标我就自由发挥了，让它们分别由正弦余弦计算得出

const points = [];
for (let i = 0; i < 30; i++) {
    const x = (Math.sin(i*0.3)+Math.cos(i*0.2))*3
    const y = (Math.sin(i*0.2)+Math.cos(i*0.3))*2
    points.push(new THREE.Vector2(x ,y));
}

然后再创建一个LatheGeometry实例，参数一已经有了，分段数目我们给它定义为24，初始位置为0，弧度为半圆，代码如下

const geometry = new THREE.LatheGeometry(
    points,
    24,
    0,
    Math.PI
);

材质直接复用刚才凸包几何体的材质，最终得到了如下的一个几何体

实在看不出它像个啥，看起来有点不太完整，这个是因为刚刚把弧度设置成了180度，这里将弧度改成360度再看看

const geometry = new THREE.LatheGeometry(
    points,
    24,
    0,
    Math.PI*2
);

那么得到的图形就是下面这个样子

有了这个几何体，以后要做点锅碗瓢盆什么的就方便多了

ExtrudeGeometry

这个几何体称为拉伸几何体，专门用它将一个2D图形拉伸成3D图形，老规矩，想使用它的话先要了解下如何构造它

export class ExtrudeGeometry extends BufferGeometry {
 constructor(shapes?: Shape | Shape[], options?: ExtrudeGeometryOptions);
}

拉伸几何体的构造函数接收两个参数，一个是Shape或者Shape的数组，也就是要被拉伸的2D图形，那么先来创建一个Shape实例

const shape = new THREE.Shape();
shape
    .moveTo(-8, 8)
    .lineTo(0, 16)
    .lineTo(8, 8)
    .lineTo(16, 8)
    .lineTo(0, -24)
    .lineTo(-16, 8);

随意画了几根线，组成一个四角星的形状，然后再来看ExtrudeGeometry构造函数的第二个参数是个ExtrudeGeometryOptions，它可以配置拉伸2D图形所需要的属性,当然也可以不设置它，直接去拉伸图形

const geometry = new THREE.ExtrudeGeometry(shape);
const extrudeObject = new THREE.Mesh(geometry, material);
scene.add(extrudeObject);

就得到了一块像这样的一个四角星图形，它看起来很薄没有怎么拉伸的原因是因为它默认的拉伸长度就为1，现在我们来了解下ExtrudeGeometryOptions的属性

depth

需要拉伸的深度，拉伸的方向是沿着Z轴，默认值为1，可以通过这个属性来控制拉伸的长度，比如这边将depth设置为5

const geometry = new THREE.ExtrudeGeometry(shape,{depth:5});

就会得到一块比较厚的四角星图形

steps

这个值的意思是拉伸体沿着拉伸方向分成了多少段，比如在上述的例子的基础上，我们再设置个steps看看有什么效果

const geometry = new THREE.ExtrudeGeometry(shape,{
    depth:5,
    steps:8
});

是不是感觉没啥区别啊，其实steps这个属性是要将图形的线框打开才能看出来效果，当我们将材质里面的wireframe设置为true之后，设置的steps就能看出来效果了

如图所示，拉伸方向分成的段数就如同steps设置的一样被分成了8段，而当我们将steps设置为2的时候，段数就不一样了

const geometry = new THREE.ExtrudeGeometry(shape,{
    depth:5,
    steps:2
});

steps的用法已经知道了，再来看下一个

bevelThickness

这个是倒角的厚度，啥叫倒角，我们可以看下生成的拉伸图形，它有前后两面，中间这段是我们拉伸的部分，倒角就是这拉伸区域与前后两面之间的厚度，默认值为0.2，有点小，我们可以把图形放大看就能看到倒角了

就是这个区域，我们可以通过设置bevelThickness这个值来改变这个区域的大小，比如设置为1.2

const geometry = new THREE.ExtrudeGeometry(shape,{
    depth:5,
    bevelThickness:1.2,
  });

现在不用放大图形也能看到倒角了，同时也注意到了一点，那就是前后倒角都有分段，而且都是三个，这个数量能否设置呢，就要看另一个属性了

bevelSegments

倒角的分段数，默认为3，这个值越大，倒角就会看起来越光滑，比如将它设置为

const geometry = new THREE.ExtrudeGeometry(shape,{
    depth:5,
    bevelThickness:1.2,
    bevelSegments:12
  });

分段数就没那么明显了，倒角变得光滑了许多

bevelSize

这个值控制倒角的大小，默认值为0.2，如果增加这个值的大小，倒角会变大，相对应的整个图形高度也会变大，比如我们将倒角高度设置为4.8

const geometry = new THREE.ExtrudeGeometry(shape,{
    depth:5,
    bevelThickness:1.2,
    bevelSegments:12,
    bevelSize:4.8
  });

bevelEnabled

这个是控制是否启用倒角的开关，默认值为true,表示启用，当设置为false的时候，无论如何去设置其他倒角的属性，都是无效的，比如在上述代码中，已经设置了几个倒角的属性了，但是当把开关bevelEnabled关闭之后，所有倒角相关属性都会无效

const geometry = new THREE.ExtrudeGeometry(shape,{
    depth:5,
    bevelThickness:1.2,
    bevelSegments:12,
    bevelSize:4.8,
    bevelEnabled:false
});

TubeGeometry

管道几何体，使用一些顶点坐标然后将其拉伸为一根管道，所以如果想要创建一个管道几何体，首先需要创建几个顶点

const points = [new THREE.Vector3(-10, 0, 10),
    new THREE.Vector3(-5, 5, 5),
    new THREE.Vector3(0, 0, 0),
    new THREE.Vector3(5, -5, 5),
    new THREE.Vector3(10, 0, 10),
    new THREE.Vector3(10, 5, 15),
    new THREE.Vector3(15, -5, 18)]

有个顶点之后，不能立刻作为参数传入TubeGeometry构造函数内，还必须通过这些点转换成一个Curve对象，这里以CatmullRomCurve3为例

const curve = new THREE.CatmullRomCurve3(points);

接着才可以正式创建TubeGeometry,代码如下

const geometry = new THREE.TubeGeometry(
    curve,
);
const extrudeObject = new THREE.Mesh(geometry, material);
scene.add(extrudeObject);

一根管道就做好了

TubeGeometry的构造函数除了接受一个CatmullRomCurve3之外，还会接收其他参数，来认识一下

tubularSegments

整根管道被分成的段数，默认为64段，当我们把这个值缩小为20的时候，段数就少了

const geometry = new THREE.TubeGeometry(curve,20);

radius

管道的粗细，这个很好理解，现在的粗细是默认值1，当把这个值改成5之后，我们就得到了一个略微粗的管道

const geometry = new THREE.TubeGeometry(curve,20,5);

radialSegments

这个是管道横截面上分的段数，默认为8，段数越多，横截面就越圆，比如将这个值设置为4，那么横截面就变成了一个正方形

const geometry = new THREE.TubeGeometry(curve,20,5,4);

而设置的多一些比如32，横截面就变成了圆形

const geometry = new THREE.TubeGeometry(curve,20,5,32);

closed

最后一个参数closed,表示管道两头是否相连，默认是不连在一起的，可以将它设置为true,那么我们的管道就变成了一个闭环了

const geometry = new THREE.TubeGeometry(curve,20,5,32,true);

ParametricGeometry

如果想要创建一些比较复杂的，无法使用常规方式创建的几何体，那么ParametricGeometry将会是一个不错的选择，在这个几何体的构造函数中，总共接受三个参数，分别是

• func：创建几何体的主要函数，该函数通过参数里面的u,v值来定义每一个顶点的位置，u,v值分别表示x，z轴上的向量，target就表示需要被计算的顶点
• slices：表示u值应该被分成多少段，数字越大，越光滑
• stacks：表示v值应该被分成多少段，数字越大，越光滑

这个几何体参数不多，也很好理解，难就难在你要有足够好的数学功底，去计算出不同的顶点坐标形成不同的造型，我们来个简单的，来做个球

const geometry = new ParametricGeometry((u,v,target)=>{
    const theta = u * Math.PI * 2; // 0到2π
    const phi = v * Math.PI; // 0到π
    const radius = 25;
    const x = radius * Math.sin(phi)* Math.cos(theta);
    const y = radius * Math.sin(phi)* Math.sin(theta);
    const z = radius * Math.cos(phi);
    return target.set(x, y, z);
},30,30)
const material = new THREE.MeshStandardMaterial({
    color: 0x9400d3,
    metalness: 0.5,
    roughness: 0.4,
});
const mesh = new THREE.Mesh(geometry, material);
scene.add(mesh);

函数内部radius表示球的半径，然后分别使用正弦余弦函数来计算出x,y,z的坐标，最终得到如下一个球

现在这样一个球其实我们也看不出顶点有几个，可以适当的给x,y,z增减点值，这样每个顶点都不会在同一个球面上，就容易看得出来

const geometry = new ParametricGeometry((u,v,target)=>{
    const theta = u * Math.PI * 2; // 0到2π
    const phi = v * Math.PI; // 0到π
    const radius = 25;
    const x = radius * Math.sin(phi)* Math.cos(theta)+Math.random()*3;
    const y = radius * Math.sin(phi)* Math.sin(theta)+Math.random()*4;
    const z = radius * Math.cos(phi)+Math.random()*5;
    return target.set(x, y, z);
},30,30)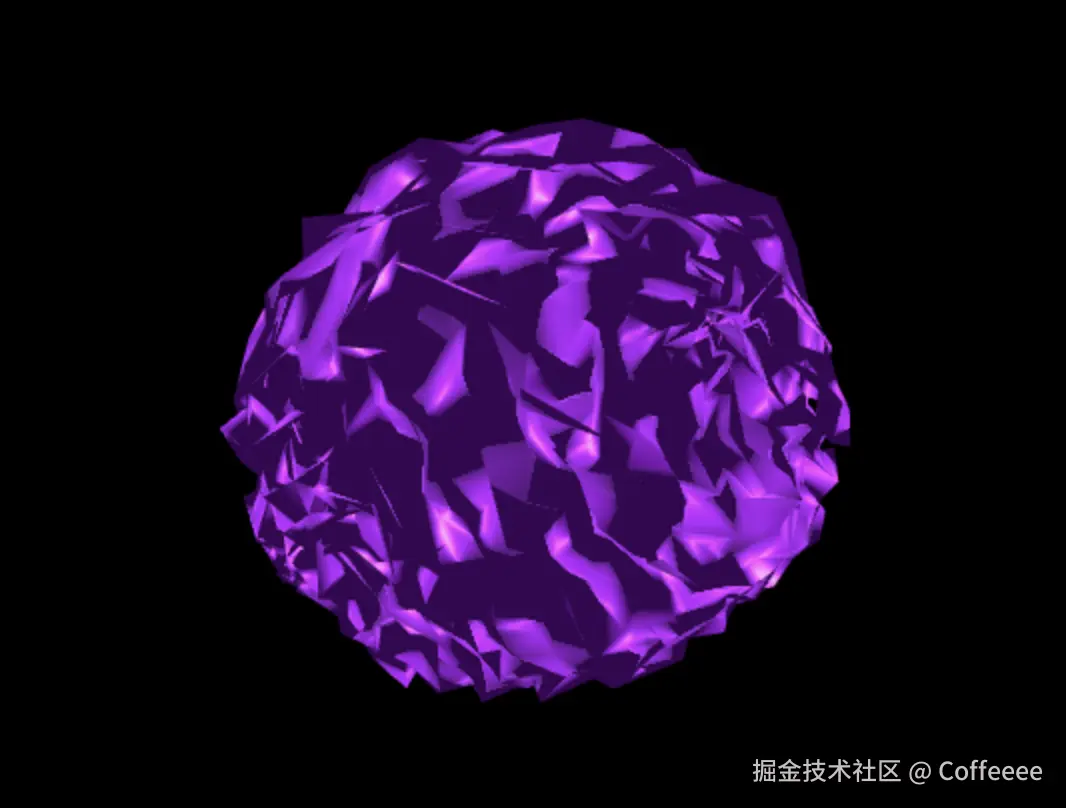

现在这个球面就显的褶皱的多了，每一个褶皱就相当于一个顶点，当我们更改slices与stacks的值的时候，褶皱的数量也会相应的改变

const geometry = new ParametricGeometry((u,v,target)=>{
    const theta = u * Math.PI * 2; // 0到2π
    const phi = v * Math.PI; // 0到π
    const radius = 25;
    const x = radius * Math.sin(phi)* Math.cos(theta)+Math.random()*3;
    const y = radius * Math.sin(phi)* Math.sin(theta)+Math.random()*4;
    const z = radius * Math.cos(phi)+Math.random()*5;
    return target.set(x, y, z);
},10,10)

是不是感觉很方便，只需要写好一个函数，就可以创建出一个复杂的图形出来，不过我们也不能对此产生依赖，越复杂的图片意味着计算量越大，会对性能产生一定的影响，所以还是需要认真思考什么时候该用什么时候不该用

总结

讲了这么些几何体，大多数都是些基本用法，不过相对于以前学过的几何体来讲，高级几何体是略微复杂一些，需要我们花更多的时间去理解每个参数代表的意思和适用场景，不多说了，希望对各位有所帮助，拜拜～