在科学研究中,数据可视化是连接实验与理论的关键桥梁。
它不仅能够清晰地呈现实验规律,还能验证假设并支持科研决策。
Plotly作为一款强大的可视化工具,凭借其交互性、动态图表支持和灵活的可定制性,在科学领域中展现出巨大的优势。
本文将探讨如何利用 Plotly 高效展示实验数据与误差分析,从而提升科研效率。
1. 实验数据展示
1.1. 数据预处理
在进行数据可视化之前,数据的整理和格式转换是必不可少的步骤。
一般使用Python的pandas库来预处理数据。
读取和解析常用的文件格式使用:
python
import pandas as pd
# 读取 CSV 文件
data_csv = pd.read_csv('data.csv')
# 读取 Excel 文件
data_excel = pd.read_excel('data.xlsx')
# 读取 JSON 文件
data_json = pd.read_json('data.json')缺失值、异常值和重复数据的处理使用:
python
# 删除缺失值
data_csv.dropna(inplace=True)
# 去除重复数据
data_csv.drop_duplicates(inplace=True)
# 处理异常值(假设异常值为负数)
data_csv = data_csv[(data_csv['value'] >= 0)]数据的标准化和归一化可以确保数据的单位统一和量纲对齐,从而更适合可视化。
例如,可以使用MinMaxScaler或StandardScaler对数据进行归一化或标准化。
python
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
data_csv[['value']] = scaler.fit_transform(data_csv[['value']])1.2. 折线图展示
折线图和柱状图是科学数据可视化中最常用的图表类型。折线图适合展示连续变量的趋势,例如时间序列实验数据。Plotly的plotly.express.line函数可以轻松实现折线图的绘制。
假设我们有一组时间序列的实验数据,记录了不同时间点的测量值。我们将使用Plotly绘制折线图来展示这些数据的变化趋势。
python
import plotly.express as px
import pandas as pd
# 创建示例数据
df = pd.DataFrame({
'time': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
'value': [2.3, 3.5, 4.1, 5.2, 4.8, 6.0, 5.5, 7.2, 6.8, 8.0]
})
# 绘制折线图
fig = px.line(
df,
x="time",
y="value",
title="时间序列实验数据折线图",
labels={"time": "时间", "value": "测量值"}, # 自定义坐标轴标签
template="plotly_dark",
) # 使用暗色主题
# 添加一些自定义样式
fig.update_traces(line=dict(color="blue", width=2)) # 设置线条颜色和宽度
fig.update_layout(
xaxis=dict(showgrid=True, gridwidth=1, gridcolor="rgba(255, 255, 255, 0.2)"),
yaxis=dict(showgrid=True, gridwidth=1, gridcolor="rgba(255, 255, 255, 0.2)"),
font=dict(family="Arial", size=12, color="white"), # 设置字体样式
)
# 显示图表
fig.show()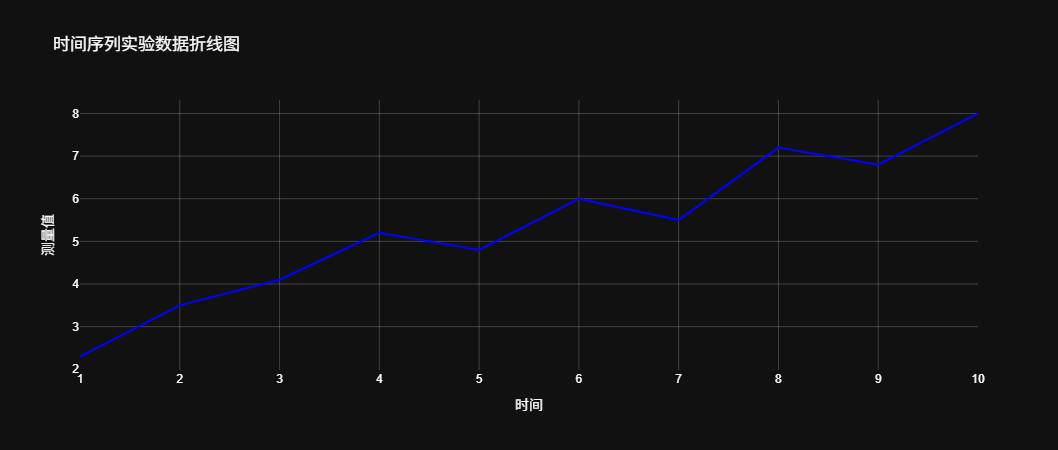
1.3. 柱状图展示
柱状图则适合对比离散实验组的结果差异,例如不同处理组的响应值。
Plotly的plotly.express.bar函数可以绘制柱状图。
在实际应用中,我们常常需要展示多组实验数据,并通过颜色编码区分对照组与实验组。
Plotly的颜色映射功能可以轻松实现这一点。
python
import pandas as pd
import plotly.express as px
df = pd.DataFrame(
{
"group": ["A", "B", "C", "D", "E"],
"response": [10, 15, 7, 12, 20],
}
)
# 绘制柱状图
fig = px.bar(
df,
x="group",
y="response",
title="不同处理组的响应值柱状图",
labels={"group": "处理组", "response": "响应值"}, # 自定义坐标轴标签
color="group", # 根据处理组分组着色
template="plotly_white",
) # 使用白色主题
# 添加一些自定义样式
fig.update_traces(
marker=dict(line=dict(color="black", width=1))
) # 设置柱子的边框颜色和宽度
fig.update_layout(
xaxis=dict(showgrid=False),
yaxis=dict(showgrid=True, gridwidth=1, gridcolor="rgba(0, 0, 0, 0.1)"),
font=dict(family="Arial", size=12, color="black"), # 设置字体样式
)
# 显示图表
fig.show()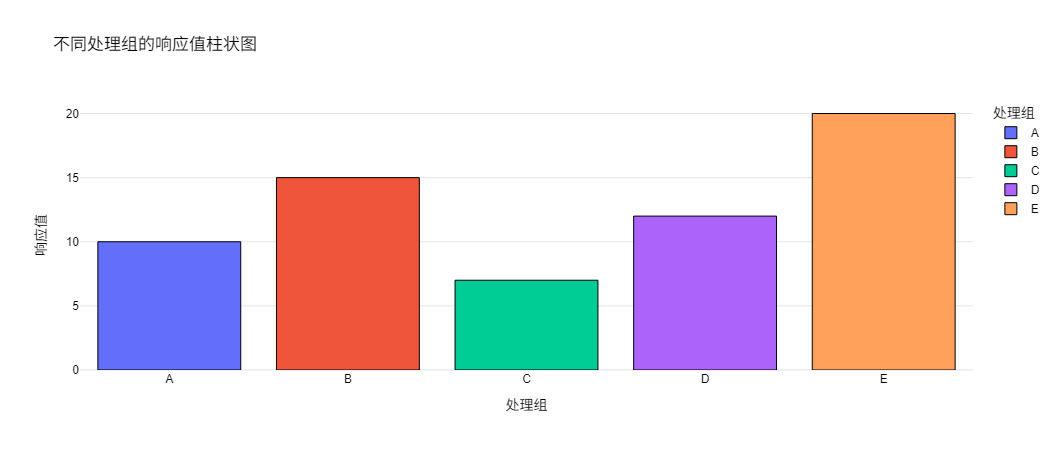
2. 误差棒的应用
误差棒是科学图表中不可或缺的元素,它能够展示数据的变异性和统计显著性。
在Plotly中,误差棒可以通过error_x和error_y参数实现。
在绘制误差棒之前,一般需要计算标准差、标准误差或置信区间。
假设我们有一组实验数据,记录了不同时间点的测量值以及每个时间点的标准差。
下面使用Plotly绘制折线图时,为每个数据点添加误差棒,以展示数据的变异性和统计显著性。
python
import plotly.express as px
# 绘制带有误差棒的折线图
fig = px.line(
df,
x="time",
y="value",
error_y="std",
title="带误差棒的时间序列折线图",
labels={"time": "时间", "value": "测量值"}, # 自定义坐标轴标签
template="plotly_dark",
) # 使用暗色主题
# 添加一些自定义样式
fig.update_traces(
line=dict(color="blue", width=2), # 设置线条颜色和宽度
error_y=dict(color="red", thickness=1.5),
) # 设置误差棒颜色和宽度
fig.update_layout(
xaxis=dict(showgrid=True, gridwidth=1, gridcolor="rgba(255, 255, 255, 0.2)"),
yaxis=dict(showgrid=True, gridwidth=1, gridcolor="rgba(255, 255, 255, 0.2)"),
font=dict(family="Arial", size=12, color="white"), # 设置字体样式
)
# 显示图表
fig.show()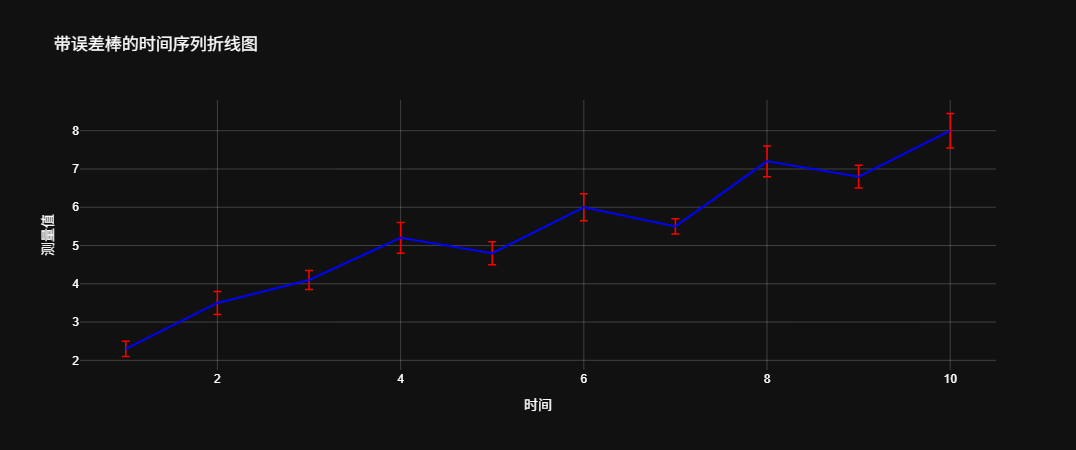
使用 Plotly 绘制柱状图,也可以为每个柱子添加误差棒。
python
import plotly.express as px
# 绘制带有误差棒的柱状图
fig = px.bar(
df,
x="time",
y="value",
error_y="std",
title="带误差棒的柱状图",
labels={"time": "时间", "value": "测量值"}, # 自定义坐标轴标签
template="plotly_white",
) # 使用白色主题
# 添加一些自定义样式
fig.update_traces(
marker=dict(
color="skyblue", line=dict(color="black", width=1)
), # 设置柱子颜色和边框
error_y=dict(color="red", thickness=1.5),
) # 设置误差棒颜色和宽度
fig.update_layout(
xaxis=dict(showgrid=False),
yaxis=dict(showgrid=True, gridwidth=1, gridcolor="rgba(0, 0, 0, 0.1)"),
font=dict(family="Arial", size=12, color="black"), # 设置字体样式
)
# 显示图表
fig.show()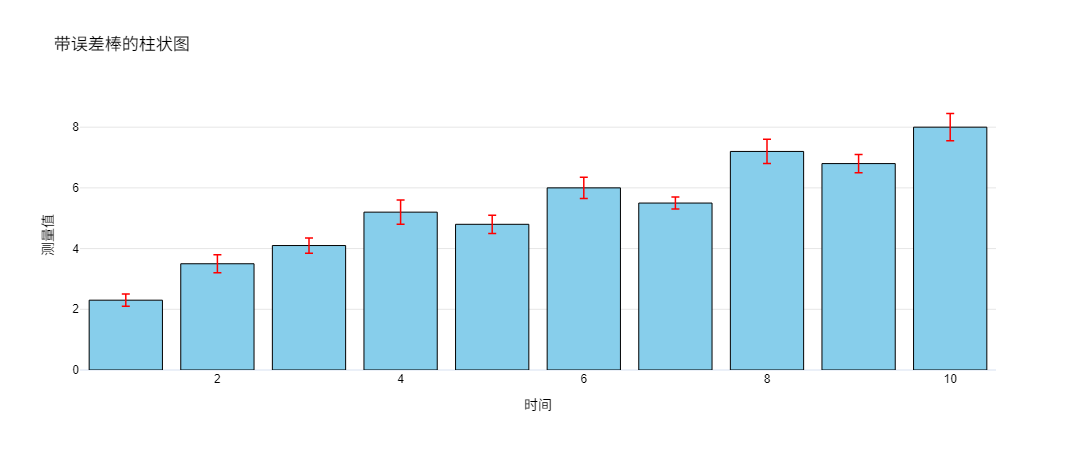
误差棒的作用主要有:
- 增强结果可信度:误差棒展示了数据的变异性和统计显著性,帮助读者理解数据的可靠性。
- 对比实验组间差异:通过观察误差范围的重叠情况,可以初步判断不同组之间的差异是否显著。
- 交互功能:Plotly 的交互功能允许用户悬停在图表上查看具体的误差数值和统计信息,例如标准差或置信区间。
3. 总结
Plotly在科学可视化中的核心价值在于它能够从数据整理到动态交互提供全流程支持。
本文主要介绍了Plotly在展示实验数据和误差分析方面的强大功能。
误差分析在科学图表中是必不可少的,而Plotly提供了灵活的实现方式。