文章目录
-
-
- [1. 题目链接](#1. 题目链接)
- [2. 题目描述](#2. 题目描述)
- [3. 题目示例](#3. 题目示例)
- [4. 解题思路](#4. 解题思路)
- [5. 题解代码](#5. 题解代码)
- [6. 复杂度分析](#6. 复杂度分析)
-
1. 题目链接
1377. T 秒后青蛙的位置 - 力扣(LeetCode)
2. 题目描述
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述,其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。
3. 题目示例
示例 1 :
plain
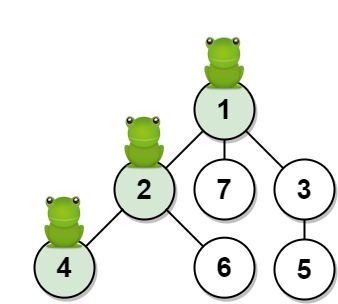
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出:0.16666666666666666
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。示例 2 :
plain
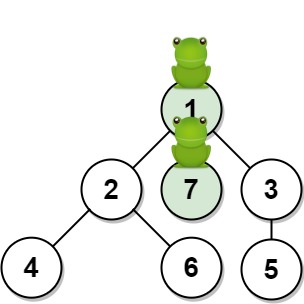
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出:0.3333333333333333
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。4. 解题思路
- 问题理解 :
- 青蛙从根节点1开始,每秒随机跳到一个子节点。
- 求t秒后青蛙位于目标节点target的概率。
- 如果时间没用完但到达叶子节点,青蛙会停在原地。
- 关键点 :
- 概率计算:每次跳跃的选择概率是1/(当前节点的子节点数)。
- 时间约束:必须在恰好t秒到达目标节点,或者提前到达但目标节点是叶子。
- 树结构:无向树,但通过DFS转化为有向树(避免回溯)。
- DFS设计 :
- 参数传递 :
prod:累积概率的倒数(即分支数的乘积),避免浮点数精度问题。leftT:剩余时间,用于判断是否恰好到达。
- 终止条件 :
- 找到目标节点且时间用完或目标节点是叶子。
- 时间用完但未找到目标节点。
- 参数传递 :
- 提前终止 :
- 一旦找到目标节点,立即返回结果,不再继续搜索。
5. 题解代码
java
class Solution {
private double ans; // 存储最终结果(青蛙位于目标节点的概率)
public double frogPosition(int n, int[][] edges, int t, int target) {
// 构建邻接表表示的树结构(节点编号从1开始)
List<Integer>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<>());
// 添加虚拟父节点0,减少根节点1的特殊判断
g[1].add(0);
// 构建无向树
for (var e : edges) {
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x);
}
// 从根节点1开始DFS搜索
dfs(g, target, 1, 0, t, 1);
return ans;
}
// DFS搜索函数
// 参数说明:
// g: 邻接表
// target: 目标节点
// x: 当前节点
// fa: 父节点(避免回溯)
// leftT: 剩余时间
// prod: 当前路径的概率乘积(即1/父节点分支数的累积乘积)
private boolean dfs(List<Integer>[] g, int target, int x, int fa, int leftT, long prod) {
// 终止条件1:当前是目标节点且(时间用完或当前是叶子节点)
if (x == target && (leftT == 0 || g[x].size() == 1)) {
ans = 1.0 / prod; // 计算概率
return true; // 找到目标
}
// 终止条件2:当前是目标节点但时间没用完且不是叶子节点
// 或者时间用完但没到达目标节点
if (x == target || leftT == 0) return false;
// 遍历当前节点的所有邻居(即子节点)
for (int y : g[x]) {
if (y != fa) { // 避免回溯父节点
// 递归搜索子节点,时间减1,概率乘积乘以分支数-1(因为要排除父节点)
if (dfs(g, target, y, x, leftT - 1, prod * (g[x].size() - 1))) {
return true; // 如果找到目标,提前终止
}
}
}
return false; // 未找到目标
}
}6. 复杂度分析
时间复杂度:O(n)
- 每个节点最多被访问一次。
- 最坏情况下需要遍历整棵树(当目标节点不存在或位于最后)。
空间复杂度:O(n)
- 邻接表存储空间:O(n)。
- 递归调用栈深度:最坏情况下(树退化为链表)为O(n)。