《从零开始入门递归算法：搜索与回溯的核心思想 + 剑指Offer+leetcode高频面试题实战（含可视化图解）》

一.递归

1.汉诺塔

题目链接：面试题 08.06. 汉诺塔问题 - 力扣（LeetCode）

题目解析：将A柱子上的盘子借助B柱子全部移动到C柱子上。

算法原理：递归

当A柱子上的盘子只有1个时，我们可以直接将A上的盘子直接移动到C上。

当A上有2个盘子时，先将1个盘子直接移动到B上（重复n=1时的做法），接着在将A上的盘子移动到C上，最后再将B上的盘子直接移动到C盘上。

当A上有3个盘子时，我们可以先将上面的2个盘子移动到B上（重复n=2时的做法），接着将A上的盘子移动到C上，最终将B上的2个盘子移动到C上（重复n=2时的做法）

最终，我们发现我们将一个大问题划分成一个子问题来解决，子问题也被划分成子问题来解决，这时候我们就可以用递归了。

温馨提示：以后看这里的时候，不用纠结递归里面的细节是怎么样的，要宏观来看待递归，坚信move(A,C,B,n-1)这个递归一定能将A上n-1个盘子全部移动到B上，move(B,A,C,n-1)这个递归一定能将B上的n-1个盘子全部移动到C上。

代码实现：

class Solution {
    public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        int n=A.size();
        move(A,B,C,n);
    }
    public void move(List<Integer> A, List<Integer> B, List<Integer> C,int n){
        if(n==1){
            C.add(A.remove(A.size()-1));
            return;
        }
        move(A,C,B,n-1);//将A上n-1个柱子借助C移动到B上
        C.add(A.remove(A.size()-1));//将A上最大的盘子移动到C
        move(B,A,C,n-1);//将剩下的n-1个盘子移动到C
    }
}

不讲武德写法：

class Solution {
    public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        for(int x: A) C.add(x);
    }
}

2.合并两个有序链表

题目链接：21. 合并两个有序链表 - 力扣（LeetCode）

题目描述：将两个有序链表合并为一个有序链表，并返回合并有序链表的头结点。

算法原理：递归算法

首先，我们找出重复的子问题，这涉及到递归函数头的设计，这道题的重复子问题就是合并两个有序链表，也就是给我们两条链表的头结点，帮我们合并两条链表，并返回合并链表的头结点。

接着，只关心一个子问题里面做什么事情，这涉及到函数体的设计，子问题的操作是先比较两条链表头结点的大小，让小的头结点作为返回值，然后再继续合并剩下的链表，如下图

假设红色1节点是我们返回的头结点，那么接下来的操作就是让合并左边剩下的节点 。

最后，我们要找出递归的出口，当某一个链表为空时，我们只需要返回另一个链表的头指针就行了。

代码实现：

这里在提醒一下，以后看这篇博客时，不要去细想递归的具体操作是什么，我们要坚信l1.next=dfs(l1.next,l2)或者l2.next=dfs(l2.next,l)能帮我们完成合并链表的操作，要用宏观的角度来看待递归

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        return dfs(list1,list2);
    }
    public ListNode dfs(ListNode l1,ListNode l2){
        if(l1==null){
            return l2;
        }
        if(l2==null){
            return l1;
        }
        if(l1.val<=l2.val){
            l1.next=dfs(l1.next,l2);//合并剩下的链表节点
            return l1;//返回头结点
        }else{
            l2.next=dfs(l2.next,l1);//合并剩下的链表节点
            return l2;//返回头结点
        }
    }
}

3.反转链表

题目链接：206. 反转链表 - 力扣（LeetCode）

题目解析：将一个链表进行翻转，并返回翻转后链表的头结点。

解法：递归

第一种递归的视角：从宏观角度看问题

在翻转链表时，如果我们先让head.next.next=head和head.next=null，但是后面继续进行翻转时，就会丢失第3个节点的信息，所以递归时不能从前往后翻转，但是，可以从前往后进行翻转，而递归就是一种从后往前进行翻转的。

此时，先让除了头结点之外的链表进行翻转，并获取到后面链表的头结点，最后在将翻转链表的头结点和head拼接起来就行了。

小细节：翻转时的head.next是为了统一操作，因为递归时，所有递归的函数的操作必须是一样的，head.next=null是为了考虑最后头结点翻转时，此时原来的头结点就是尾节点了，此时就需要将head.next=null.

代码实现：

class Solution {
    public ListNode reverseList(ListNode head) {
        return dfs(head);
    }

    public ListNode dfs(ListNode head){
        //1.递归出口
        if(head ==null || head.next == null ){
            return head;
        }
        //翻转剩余的链表并获取后面翻转链表的头结点
        ListNode newHead=dfs(head.next);
        head.next.next=head;
        head.next=null;
        return newHead;
    }
}

第二种视角：我们可以将链表看做一棵树

此时，如果我们将链表看做一棵树的话，解决此道题我们就只需要做一遍后续遍历即可，我们先遍历到叶子节点，如果遍历到叶子节点，就返回，并进行翻转。

下面这个有我的理解，后面复习一定要看下面这个图

4.两辆交换链表中的节点

题目链接：24. 两两交换链表中的节点 - 力扣（LeetCode）

题目解析：将链表中相邻的节点依次交换，只能交换节点的位置（就是修改节点的next的指向），不能通过修改节点中的值实现交换相邻节点。

算法原理：递归

先让后面的链表实现交换的操作，返回一个tmp头结点，然后再将前面两个节点进行交换，最后进行拼接就行了。

代码实现

class Solution {
    public ListNode swapPairs(ListNode head) {
        return dfs(head);
    }
    public ListNode dfs(ListNode head){
        if(head==null || head.next==null){
            return head;
        }
        ListNode tmp=dfs(head.next.next);
        ListNode newHead=head.next;//记录返回的头结点
        head.next.next=head;
        head.next=tmp;
        return newHead;
    }
}

5.快速幂

题目链接：50. Pow(x, n) - 力扣（LeetCode）

题目分析：求x的n次方。

解法一：暴力循环

直接将x乘n次，并返回最终结果，要处理n是负数的情况，会超时

代码实现：

class Solution {
    public double myPow(double x, int n) {
        double ret = 1.0;
        if (n < 0) {
            n = -n;
            for (int i = 0; i < n; i++) {
                ret *= x;
            }
            return 1.0 / ret;
        }
        for (int i = 0; i < n; i++) {
            ret *= x;
        }
        return ret;
    }
}

解法二：递归

上面那种解法为什么会超时呢？因为当n=2^31次方时，上面的解法就会循环2^31次，此时就会超时，所以，要避免循环2^31次循环的出现。

此时，没必要一次一次的进行x*x的操作，当我们知道要求x^n次方，我们先找出x^n的一半，也就是x^(n/2)，通过x^(n/2)求x^n，如下图

此时，要考虑n为奇数，n/2除不尽的情况，当n为奇数时，只需要在乘上一个x就行了。

通过上面的分析，每次求x的n次幂，都是相同的操作，都是根据x的（n/2）次方去求x的n次方，所以，每求x的n次幂就可以看做一个相同的子操问题。

每个子问题就是求x的n次方，我们用tmp来保存每次递归求x的n次方的结果，当n==0时，直接返回1即可

代码实现：

class Solution {
    public double myPow(double x, int n) {
        if(n<0){
            n=n-2*n;
            return 1.0/dfs(x,n);
        }
        return dfs(x,n);
    }
    public double dfs(double x,int n){
        if(n==0){
            return 1;
        }
        double tmp = dfs(x,n/2);
        return n%2==0?tmp*tmp:tmp*tmp*x;
    }
}

递归代码解析：dfs函数是用来递归求x的n次幂的，我们不要去细想里面的细节是如何实现的，只要我们dfs函数里面的求x的n次方实现逻辑是正确的，我们坚信dfs能求出x的n次幂即可。

二.二叉树的深度搜索

1.计算布尔二叉树的值

题目链接：2331. 计算布尔二叉树的值 - 力扣（LeetCode）

题目解析：根据题意，该题中的二叉树是完整二叉树，完整二叉树就是每个非叶子节点一定会有左子节点和右子节点，如果该非叶子节点没有左子节点，那么也不会有右子节点，如果该非叶子结点没有右子节点，那么也不会有左子节点。在该题中，完整二叉树的叶子节点的value有0（对应false）或1（对应true）这两个值，非叶子节点的value有 || 或者 && 这两个值，此时，让我们计算并返回该二叉树的布尔值。

算法原理：递归

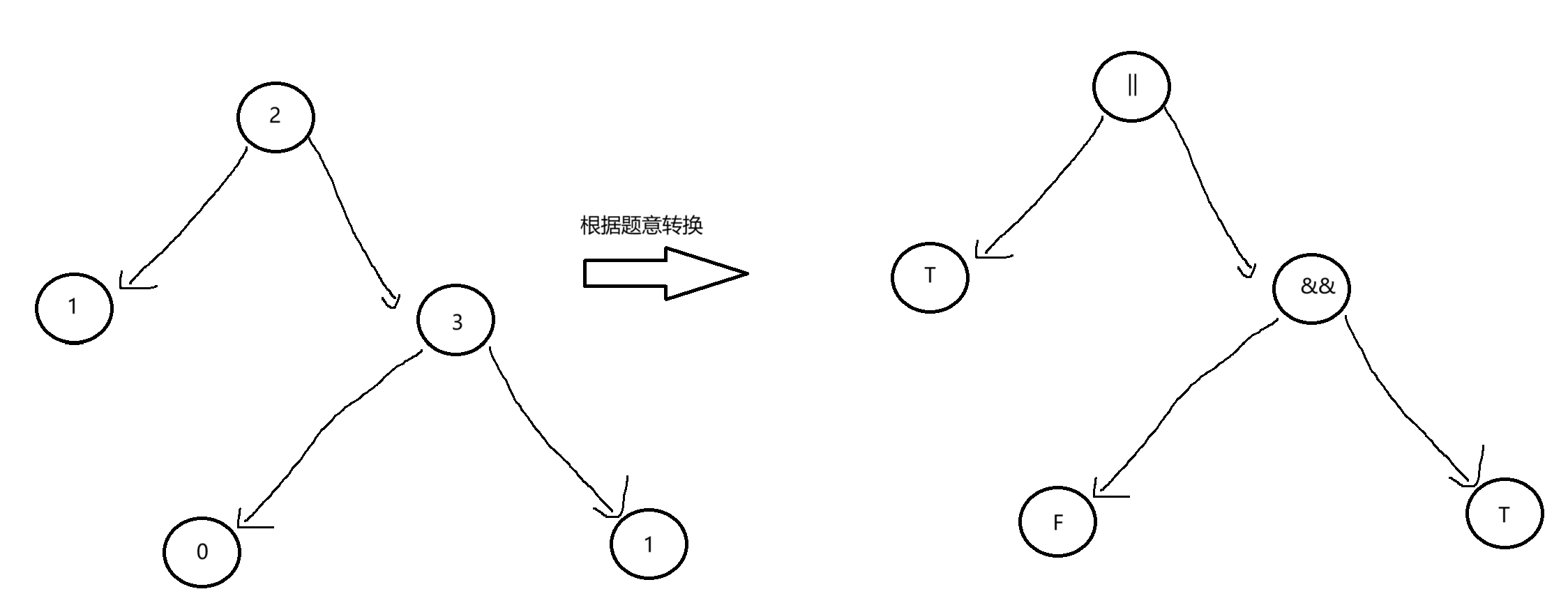
此时，为了求出整根树的布尔值，我们首先要求出左右子数的布尔值，当我们遇到叶子节点时，直接返回叶子节点的值即可，得到左右子数的布尔值之后，我们就直接返回左右子数的布尔值和根节点进行计算的结果即可。

其实也可以换一个角度来看，其实就是对完整二叉树进行一遍后续遍历，在后续遍历的过程中，计算并返回并保存左右子数的布尔值，最后在根据左右子树的布尔值和根节点的值进行计算并返回即可。

代码实现

class Solution {
    public boolean evaluateTree(TreeNode root) {
        return dfs(root);
    }
    public boolean dfs(TreeNode root){
        //遇到叶子节点
        if(root.left == null && root.right == null){
            if(root.val == 0) return false;
            else return true;
        }
        //计算左子树的布尔值
        boolean left = false;
        if(root.left != null){
            left = dfs(root.left);
        }
        //计算右子树的布尔值
        boolean right = false;
        if(root.right != null){
            right = dfs(root.right);
        }
        if(root.val == 2){
            return left || right;
        }else {
            return left && right;
        }
    }
}

2.求根节点到叶子节点的数字之和

题目链接：129. 求根节点到叶节点数字之和 - 力扣（LeetCode）

题目解析；计算从根节点到叶子节点的所有数字之和，如下图

算法原理：递归

如上图中的二叉树，假如我们现在递归到了5这个节点，要是想求出1258,12594,12593这三个数字，我们就需要得到前面的125,125怎么来的呢？是递归到5的时候，这时候我们进行一个求前驱的操作，此时得到前驱12，然后进行12*10+5就得到了125，然后再求1258,12594,12593这3个数的时候，以125作为前驱去进行相同的计算，就可以得到这三个数了，当计算出这三个数的同时，直接返回对应的数字即可。

递归的出口，当遇到叶子节点直接返回即可，注意此时递归的结束是要在求前驱的操作之后。

总结函数体的操作，先求前驱，接着判断递归条件，如递归不结束，继续去递归左子树和右子树，最后返回ret即可。

代码实现：

class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root,0);
    }
    public int dfs(TreeNode root,int presum){
        //1.求前驱
        presum = presum*10+root.val;
        //2.递归出口
        if(root.left == null && root.right == null) 
            return presum;
        //3.递归左右子数
        int ret = 0;
        if(root.left != null) ret += dfs(root.left,presum);
        if(root.right != null) ret +=dfs(root.right,presum);
        return ret;
    }
}

3.二叉树剪枝

题目链接：814. 二叉树剪枝 - 力扣（LeetCode）

题目解析：遍历二叉树，将只含数值0的子数全部去掉，返回剪枝后的二叉树。

算法原理：递归

递归函数头的设计：由于要将只含数值0的子数全部去掉，由于在删除子数的时候，此时我们要去收集左子树和右子树的信息，所以在此题中，递归的函数是要有一个返回值的，且要通过后序遍历来遍历这棵树，

在后续遍历中，我们可以先去处理左子树，再去处理右子树，分别记录左子树和右子树的情况，在处理完左子树和右子树之后，还要根据当前根节点的值去判断要不要删除该子数，如果当前根节点的值为0，我们直接返回null即可，如果根节点的值为1，直接返回该根节点即可。

递归的出口：当root==null时，返回一个null即可。

代码实现：

class Solution {
    public TreeNode pruneTree(TreeNode root) {
        return dfs(root);
    }
    public TreeNode dfs(TreeNode root){
        if(root==null){
            return null;
        }
        //处理左子树
        root.left = dfs(root.left);
        //处理右子树
        root.right = dfs(root.right);
        //判断
        if(root.val == 0&&root.left==null&&root.right==null){
            return null;
        }
        return root;
    }
}

4.验证二叉搜索树

题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

题目解析：验证该二叉树是不是二叉搜索树，如果是，则返回true，如果不是，则返回false。

算法原理：递归

由于搜索二叉树的左子树中的所有节点中的值都是小于根节点的值，右子树中的所有节点的值都是大于根节点的值。此时就可以根据二叉搜索树的中序遍历是一个升序的排列， 因此可以定义一个全局变量prev，一开始prev的值为无穷小，全局变量prev是用来记录中序遍历时的前驱。

为什么要将prev设为全局变量呢？

将prev设为全局变量，我们就不用在递归时传入这个参数，写递归代码时比计较方便。

此时，就可以在中序遍历中，如果前驱的值和当前递归到的节点的值构成递增序列，就可以让prev=root.val，为下一次递归使用。

算法流程：

递归出口：如果当前节点为null，则该子数也是二叉搜索树，直接返回true。

递归逻辑：由于是中序遍历，我们先判断当前节点的左子树是不是二叉搜索树（用left变量来记录），然后再去判断当前节点是否与左子树构成二叉搜索树（用cur来记录），最后在判断当前节点的右子树是不是二叉搜索树（用right类记录）。

代码实现：

class Solution {
    //前驱
    long prev=Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        return dfs(root);
    }
    public boolean dfs(TreeNode root){
        //递归出口
        if(root == null){
            return true;
        }
        //判断左子树是不是二叉搜索树
        boolean left = dfs(root.left);
        //判断当前节点是不是二叉搜索树
        boolean cur = false;
        if(root.val>prev) cur = true;
        prev = root.val;
        //判断右子树是不是二叉搜索树
        boolean right = dfs(root.right);
        return left && cur && right;
    }
}

小优化：剪枝

如果我们在中序遍历时，发现左子树不是二叉搜索树 或者 当前节点不与左子树构成二叉搜索树时，这时就没必要再去遍历右子树，直接返回false即可。

代码实现：

其实就是在原来的代码上加上几个判断即可。

class Solution {
    long prev=Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        return dfs(root);
    }
    public boolean dfs(TreeNode root){
        //递归出口
        if(root == null){
            return true;
        }
        //判断左子树是不是二叉搜索树
        boolean left = dfs(root.left);
        //剪枝
        if(left == false) return false;
        //判断当前节点是不是二叉搜索树
        boolean cur = false;
        if(root.val>prev) cur = true;
        //剪枝
        if(cur == false) return false;
        prev = root.val;
        //判断右子树是不是二叉搜索树
        boolean right = dfs(root.right);
        return left && cur && right;
    }
}

5.二叉搜索树中第k小的元素

题目链接：230. 二叉搜索树中第 K 小的元素 - 力扣（LeetCode）

题目解析：找出并返回二叉搜索树中的第k小的元素。

算法原理：深度搜索

在此道题中还是可以使用二叉搜索树的中序遍历是一个升序的序列，此时，我们就可以定义两个全局变量count和ret，count是用来计数的，ret是用来保存最终结果的。

中序遍历时， 当我们遍历到一个节点时，先让count--，知道count==0时，遍历的节点的值就是题目要求寻找的值，直接让ret==root.val。

剪枝优化

当递归时发现count已经递减为0了，就没必要继续遍历剩下的节点了，直接返回即可。

class Solution {
    int count;
    int ret;
    public int kthSmallest(TreeNode root, int k) {
        count = k;
        dfs(root);
        return ret;
    }
    public void dfs(TreeNode root){
        //递归出口和剪枝优化
        if(root==null || count==0) return;
        dfs(root.left);
        count--;
        if(count==0) ret = root.val;
        //剪枝优化
        if(count==0) return;
        dfs(root.right);
    }
}

一个小收货

当我们将count和ret设计为全局变量，此时，我们设计递归的函数时，就不用考虑设计递归函数的返回值和其他多余的传参等，这样写递归函数的时候就很方便。

6.二叉树的所有路径

题目链接：257. 二叉树的所有路径 - 力扣（LeetCode）

题目解析：找出并返回每一条从根节点到叶子节点的路径。

讲解算法原理：在这道题中，我们主要分析全局变量，回溯（恢复现场）和剪枝这三点。

我一开始的做法，我首先创建了2个全局变量，一个ret（返回结果）和一个path（用来记录从根节点到也叶子节点的路径），但是这样会有一个问题，就是当我们遍历完一个左子树时，会去遍历右子树，遍历右子树时，由于path会带着左子树的叶子节点，这样会导致遍历右子树的路径不正确。如下图

所以我们在回溯的过程中，要进行恢复现场，也就是在回溯去遍历右子树时，要将path恢复成1->2->,此时在去遍历右子树。所以在这道题中，将path设置为全局变量并不好用。

但是，我们可以将path设置为函数的参数去进行递归，此时，我们可能会写出以下代码

class Solution {
    List<String> ret = new ArrayList();
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root,new StringBuffer(""));
        return ret;
    }
    public void dfs(TreeNode root,StringBuffer path){
        //StringBuffer path = new StringBuffer(_path);
        path.append(root.val);
        if(root.left == null && root.right == null){
            ret.add(path.toString());
        }
        path.append("->");
        if(root.left != null) dfs(root.left,path);
        if(root.right != null) dfs(root.right,path);
    }
}

但是，这个代码是有bug的，运行如下图，我们发现并没有起到恢复现场的作用，因为此时，我们将path作为参数时，每次递归也是直接对path进行append，此时path就无法记录上一层path的情况，所以此时，可以另外设计一个变量，让新设计的变量去进行每一次递归的append操作，这样我们就没有直接对每一层的path进行append，此时，递归的每一层都会有一个path来记录每一层的路径（每一层的path不是同一个东西），这样在回溯时，path就起到一个恢复现场的作用。

正确代码实现：

//剪枝优化版本
class Solution {
    List<String> ret = new ArrayList();
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root,new StringBuffer(""));
        return ret;
    }
    public void dfs(TreeNode root,StringBuffer _path){
        StringBuffer path = new StringBuffer(_path);
        path.append(root.val);
        if(root.left == null && root.right == null){
            ret.add(path.toString());
        }
        path.append("->");
        if(root.left != null) dfs(root.left,path);
        if(root.right != null) dfs(root.right,path);
    }
}


//未剪枝优化版本
class Solution {
    List<String> ret = new ArrayList();
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root,new StringBuffer(""));
        return ret;
    }
    public void dfs(TreeNode root,StringBuffer _path){
        if(root == null) return;
        StringBuffer path = new StringBuffer(_path);
        path.append(root.val);
        if(root.left == null && root.right == null){
            ret.add(path.toString());
        }
        path.append("->");
        dfs(root.left,path);
        dfs(root.right,path);
    }
}


//我写的版本
class Solution {
    List<String> ret = new ArrayList();
    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root,"");
        return ret;
    }
    public void dfs(TreeNode root,String path){
        if(root == null) return;
        StringBuilder sb = new StringBuilder();
        if(root.left == null && root.right == null){
            sb.append(path+root.val+"");
            path=sb.toString();
            ret.add(path);
        }
        sb.append(path+root.val+"->");
        path=sb.toString();
        dfs(root.left,path);
        dfs(root.right,path);
    }
}

我写的版本中，sb变量起到进行append的1作用

此时，我们通过_path去记录上一层路径的情况，让新设计的path去进行每一次遍历的append，如下图

三.穷距vs暴搜vs深搜vs回溯vs剪枝

1.全排列

题目链接：46. 全排列 - 力扣（LeetCode）

题目解析：找出并nums数组中所有的全排列组合

算法原理： 递归（涉及回溯）

涉及到一些复杂的递归问题，第一步我们可以画出决策树，越详细越好。

接着来设计代码，当我们画出策略树，我们就看看如何使用这个策略树。

首先，我们要定义一个全局变量ret去记录找到的所有的全排列组合，由于要在遍历策略树时保存排列情况，所以还要设计一个path去记录递归时的排列变化情况，如下面画红框部分，用记录递归到每一层的排列变化情况。

此时，还有一个问题，遇到了重复数字怎么办？

此时，还要设计一个全局变量checked去记录已经进行排列的数字， 当一个数字已经进行排列，我们就将其对应的check[i]置为false。

所以，此时，要去判断一下该数字是否已经在排列组合中了，不在排列组合中，才将该数字插入到path。

细节问题：

1.回溯

回溯时，要将path的最后一个元素给干掉，还要修改其对应的check数组的值。

2.递归出口

当遇到叶子节点（path的长度等于nums的长度）时，说明此时已经出现一种全排列组合，直接往ret中add即可。

代码实现

class Solution {
    List<List<Integer>> ret;
    List<Integer> path;
    boolean[] check;
    public List<List<Integer>> permute(int[] nums) {
        ret = new ArrayList<>();
        path = new ArrayList<>();
        check = new boolean[nums.length];
        dfs(nums);
        return ret;
    }
    public void dfs(int[] nums){
        //递归出口
        if(path.size() == nums.length){
            ret.add(new ArrayList<>(path));
            return;
        }
        for(int i=0;i<nums.length;i++){
            if(check[i]==false){
                path.add(nums[i]);
                check[i]=true;
                dfs(nums);
                //回溯->恢复现场
                path.remove(path.size()-1);
                check[i]=false;
            }
        }
    }
}

2.子集

题目链接：78. 子集 - 力扣（LeetCode）

题目解析：找出并返回nums数组中的所有子集。

算法原理：递归

找子集可以理解为我们选或者不选nums数组中的一个数来组成一个集合，此时，就可以设计决策树，如下图，

此时，按照选或者不选nums中一个数字组成子集的思路，发现画出来的叶子节点就是我们想要找的子集

此时，我们就可以设计代码了，去设计全局变量，设计dfs和处理一些细节问题（剪枝，回溯，递归出口）

在这道题中，要设计两个全局变量，分别设计一个path变量去记录遍历决策树时子集的组成情况和设计一个ret去存储nums中可以组成的子集。

dfs函数的设计

函数头的设计：由于我们要知道每一层递归时要选择或者不要选择的数组，所以此时在设计函数头时还要传一个下标index。

函数体的设计：根据上面的分析，遍历到策略树的每一层时，会有2中情况。第一种情况：如果我们选择这个数字，我们就要将这个数字尾插到path中（path.add(nums[index])）, 尾插完这个数字后，还要递归到下一层。第二种情况：如果我们不选择这个数字，直接递归到下一层即可，不过，此时要进行回溯，因为path是随时在改变的，所以每次返回时，我们都要将path还原成原来的样子，否则就会出现下图篮框的情况。

递归出口的设计，当遇到叶子节点时，直接返回，并且向ret中添加结果。

代码实现：

class Solution {
    List<List<Integer>> ret;
    List<Integer> path;
    public List<List<Integer>> subsets(int[] nums) {
        ret = new ArrayList<>();
        path = new ArrayList<>();
        dfs(nums,0);
        return ret;
    }
    public void dfs(int[] nums,int index){
        //递归出口
        if(index == nums.length){
            ret.add(new ArrayList<>(path));
            return;
        }
        //选
        path.add(nums[index]);
        dfs(nums,index+1);
        path.remove(path.size()-1);
        //不选
        dfs(nums,index+1);
    }
}

写代码时一个非常细节的细节，就是往ret中添加结果中是ret.add(new ArrayList<>(path))而不是直接ret.add(path)，因为path存储的是引用（也就是此时ret存储的path都是同一个东西，ret里面的path都是同一个引用，会同时指向同一个值，也就是到最后，ret中存储的path的值都是相同的），如果我们直接存储path，后面我们会修改path，也会影响ret里面的path指向的值，如下图

所以，在ret.add时，存储的是path的副本，也就是ret.add(new ArrayList<>(path))这种写法。

解法二：按照子集中数字的个数来找

上面那种解法是按照选或者不选这个数字的思路来寻找nums数组中所有子集，此时我们也可以按照子集中数字的个数的思路去寻找nums数组中子集的个数，按照此思路画出决策树

此时按照策略树去设计函数，分别设计一个path变量去记录遍历决策树时子集的组成情况和设计一个ret去存储nums中可以组成的子集。

函数头的设计，此时依旧传一个index变量，index变量表示该层递归是从哪一层开始的。

函数体的设计，在这个思路中，我们是一进入递归就要ret中添加结果，往ret中添加完结果后，就直接去递归到下一层,返回时在进行一个回溯就行了。

class Solution {
    List<List<Integer>> ret;
    List<Integer> path;
    public List<List<Integer>> subsets(int[] nums) {
        ret = new ArrayList<>();
        path = new ArrayList<>();
        dfs(nums,0);
        return ret;
    }
    public void dfs(int[] nums,int index){
        ret.add(new ArrayList<>(path));
        for(int i=index;i<nums.length;i++){
            path.add(nums[i]);
            dfs(nums,i+1);
            path.remove(path.size()-1);//回溯
        }
    }
}

写代码时一个非常细节的细节

就是当我们dfs时是dfs(nums,i+1)这种写法，不能写成dfs(nums,i++)，因为i++是直接对递归到这层的i的值进行了修改 ，后面返回到这一层时还要用到这一层的i，由于在递归时修改了原来i的值，所以后面再去使用i时，结果就会出错。