相机将3D世界映射到2D图像,相机模型描述了这种映射,主要相机模型包括 finite camera 和 infinite camera。
1 Finite Projective Camera

如上图所示,Finite Projective Camera 是焦距f为有限值的相机模型,这是一个针孔模型,其几何元素描述如下:
.像平面(image plane):2D图像成像平面
.相机中心(camera centre):点C位置,为坐标系中心
.主轴(principal axis):Z轴方向
.像主点(principal point):主轴与像平面的交点,图像上为p点
.主平面(principal plane):XY轴平面
.轴平面(axis plane):相机中心与像平面上任意一个坐标轴构成的平面
根据以上几何关系,三维空间上点X投影到像平面上点x,其关系如下:
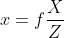
,

以上运算是一个非线性变换,计算机擅长线性运算,使用齐次坐标可以将以上运算修改为线性运算:
令三维空间点齐次坐标为

,使用矩阵

对其进行变换得

,这是二维平面点的齐次表示。
将相机成像等效表达为矩阵变换x=PX,这就建立了相机成像的数学模型。
在以上表达基础上考虑像主点(principal point)偏移,其变换为

,
使用矩阵表达为

,该变换矩阵的自由度为3。
到目前为止,对三维点施加矩阵P进行线性变换得到的图像坐标单位与三维点单位一致,如米,毫米等。
欲将其转换为像素坐标,需要考虑:
1)对其乘以一个系数变换到像素单位;
2)像元可能是长方形,所以在XY方向上系数可能不一致;
变换矩阵P可写作

,该矩阵的自由度增加到4。
考虑到像平面xy轴可能并不严格正交,因此需要增加一个扭曲变换(skew),
变换矩阵表示为

,该矩阵的自由度增加到5。
变换矩阵P的所有有效信息为左边3*3上三角矩阵,将其单独提取处理表示为

,
x=PX可改写为

,这里使用

代替X强调了该三维空间坐标是以相机中心为原点建立起来的坐标系(如上图)。
**接下来需要引入世界坐标系,**其目的是将任意世界坐标下的三维点映射到图像平面,

如上图所示,右边是任意世界坐标,左边是相机坐标,世界坐标系上任意一点转换到相机坐标需要如下步骤:
1)将世界坐标系平移 -C,其中C是相机中心在世界坐标系上的坐标值;
2)以C为中心,绕XYZ轴旋转合适的角度使得世界坐标与相机坐标重合;
以上变换可表示为

,R为旋转矩阵,三维旋转可参考 三维旋转 - 罗飞居 - 博客园 (cnblogs.com)
将其整理成齐次变换为

。
因此,对任意世界坐标系下三维坐标点,投影到像平面由以下步骤完成:
1)将世界坐标变换到相机坐标,2)在相机坐标下将三维空间点投影到二维图像平面,
整合成矩阵表达为

,此时,X为任意世界坐标系下点,x为相平面坐标点。
变换矩阵

增加了3个平移自由度和3个旋转自由度,该矩阵一共有11个自由度。
矩阵K表达了相机相关属性,为相机内参,矩阵R,C表达了世界坐标系与相机坐标之间的关系,称为相机外参。
一个3*4的矩阵包含了12个元素,由于一组各元素比值相同的变换对应一个齐次变换,因此该矩阵正好包含了11个自由度,
所以,任意一组各元素比值一致的3*4矩阵确定了一个唯一的有限投影相机变换!
2 通过投影变换矩阵获得相机信息

投影变换矩阵是以上模型的数学描述,当变换矩阵P已知时,可以得到模型中各元素的相关信息。
1)相机中心(camera centre)
相机中心C(欧式坐标)由变换矩阵P的零空间确定,理由如下:
对C点施加变换P可表示为

,

为投影矩阵的零空间。
2)列空间
将变换矩阵P表示为

,则

分别表示世界坐标系下XYZ坐标轴在图像上的消失点(vanishing point),
考察对X轴上无穷远点

施加矩阵P变换得到

,将X轴上无穷远点映射到一个图像点

,对其他轴也有类似的结论。
而

则为世界坐标上零点到图像平面的映射点。
3)行空间
将变换矩阵P表示为行向量组合

,则

确定了主平面(principal plane),理由如下:
主平面是经过相机中心且平行于像平面的平面(XY平面),很显然该平面上任意点都投影到像平面的无穷远点,
即

,进一步有

,因此

确定了主平面。

分别确定了不同的轴平面(axis plane),理由如下:
考虑三维空间点满足

,则矩阵变换满足

,因此三维空间点被投影到像平面y轴上,
同时有相机中心点C满足约束

,因此

定义了相机中心到图像坐标y轴构成的平面。
同理,

定义了相机中心到图像坐标x轴构成的平面。
通过以上平面信息,还可以获得变换矩阵的一些重要性质:
.添加约束

,使得像平面正交,

表示像平面x轴,

表示像平面y轴;
.添加约束

,使得像元为正方形,等号两边分别表示像平面坐标轴方向上的单位向量模值;
4)像主点(principal point)与主轴(principal axis)
在求像主点和主轴时,对变换矩阵P进行适当改写更加方便描述,令

,

,
像主点是相机中心到像平面上的投影点,既然

确定了主平面,且主平面与像平面平行,
则像平面的法向量为

的前三个元素

构成,在法向量上无穷远点为

,
对该点投影到像平面为

。
已知像平面的法向量为

,法向量方向可以通过考察在相机坐标系下变换得到,即

。
3 三维点与二维点映射关系
1)已知三维空间点X,通过变换x=PX可以得到在像平面上的投影点,对于无穷远点

,
有

,因此仅有3*3子矩阵影响了无穷远点映射。
2)已知图像上点x,根据相机模型,无法确定一个唯一的三维点,但可以确定一条经过相机中心到无穷远点的射线,
在该射线上的任意点(除相机中心)都能映射到x。
将变换矩阵可等价表示为

,
得到相机中心的欧式坐标为

;
同时图像上点x被映射到三维空间上一条射线,该射线与无穷远平面相交为

,
反过来看则

被变换矩阵P映射到图像点x,即

,
对于finite projective camera,其变换矩阵的秩为3,子矩阵M为满秩矩阵,因此有

,

;
综上得到三维映射射线为

。
4 Affine Camera(Infinite Camera)
仿射相机的相机变换矩阵P的最后一行为

,该变换下无穷远点被映射到无穷远点。
仿射相机可以在finite projective camera基础上对焦距(flocal length)和相机到物体的距离求极限得到。
finite projective camera的变换矩阵可重写为

,
给定一个时间变量t,当t从0开始增加时,相机中心沿着主轴慢慢远离物体,
可表示为

;
当相机原理时,成像会变小,考虑增加焦距以抵消相机远离,同时为了让成像保持大小不变,
令

,将焦距增加到

,
得到

,
当t趋近无穷大时,有

,即为仿射相机矩阵。