
一个MATLAB 实现,用于解决垃圾运输路径优化问题。该代码基于前文思路,能够直接运行,并输出最优路径、车辆分配和总行驶距离等结果。
文章目录
一个城区有 n = 30 个垃圾分类收集点,每日产生厨余垃圾,需由专用车辆运输到垃圾处理厂。要求最小化每日总行驶距离,确定:
- 使用的车辆数量;
- 每辆车的运输路径及任务分配(即,哪些收集点由哪辆车负责);
- 每趟运输的具体路线。
输入数据包括:
- 垃圾收集点编号、坐标、每日垃圾产生量;
- 车辆最大载重 Q = 5 Q = 5 Q=5吨;
- **垃圾处理厂编号,车辆从垃圾处理厂出发并返回。
数学模型的建立
决策变量
- x i j k ∈ { 0 , 1 } x_{ijk} \in \{0, 1\} xijk∈{0,1}:若车辆 k k k从点 i i i行驶到点 j j j,则 x i j k = 1 x_{ijk} = 1 xijk=1,否则为 0。
- q i k q_{ik} qik:车辆 k k k 在点 i i i装载的垃圾量(吨)。
参数
- c i j c_{ij} cij:从点 i i i到点 j j j的行驶距离(欧氏距离)。
- Q Q Q:车辆最大载重,单位吨。
- d i d_i di:点 i i i的垃圾产生量(吨)。
- n n n:垃圾收集点数量(不含垃圾处理厂)。
目标函数
最小化所有车辆的总行驶距离:
min ∑ k ∑ i = 0 n ∑ j = 0 n c i j ⋅ x i j k \min \sum_{k} \sum_{i=0}^{n} \sum_{j=0}^{n} c_{ij} \cdot x_{ijk} mink∑i=0∑nj=0∑ncij⋅xijk
约束条件
- 每个垃圾点的需求必须被满足 :
∑ k ∑ j = 0 n x i j k = 1 , ∀ i = 1 , ... , n \sum_{k} \sum_{j=0}^{n} x_{ijk} = 1, \quad \forall i = 1, \dots, n k∑j=0∑nxijk=1,∀i=1,...,n - 车辆流量守恒 (防止断路):进入和离开的流量相等:
∑ j = 0 n x i j k = ∑ j = 0 n x j i k , ∀ k , ∀ i = 1 , ... , n \sum_{j=0}^{n} x_{ijk} = \sum_{j=0}^{n} x_{jik}, \quad \forall k, \forall i = 1, \dots, n j=0∑nxijk=j=0∑nxjik,∀k,∀i=1,...,n - 车辆载重限制 :
q i k ≤ Q , ∀ i , ∀ k q_{ik} \leq Q, \quad \forall i, \forall k qik≤Q,∀i,∀k - 装载量平衡 :
q j k = q i k + d j ⋅ x i j k , ∀ i , j = 1 , ... , n , ∀ k q_{jk} = q_{ik} + d_j \cdot x_{ijk}, \quad \forall i, j = 1, \dots, n, \forall k qjk=qik+dj⋅xijk,∀i,j=1,...,n,∀k - 车辆始终从垃圾处理厂出发并返回 :
∑ j = 1 n x 0 j k = 1 , ∑ j = 1 n x j 0 k = 1 , ∀ k \sum_{j=1}^{n} x_{0jk} = 1, \quad \sum_{j=1}^{n} x_{j0k} = 1, \quad \forall k j=1∑nx0jk=1,j=1∑nxj0k=1,∀k - 变量定义 :
x i j k ∈ { 0 , 1 } , q i k ≥ 0 x_{ijk} \in \{0, 1\}, \quad q_{ik} \geq 0 xijk∈{0,1},qik≥0
算法设计与求解
求解算法:基于启发式的分批运输优化
由于问题为 NP难问题(类似车辆路径问题,VRP),使用精确算法(如整数规划)在大规模情况下时间复杂度过高。我们设计启发式算法结合分批运输思想求解。
算法步骤:分批运输 + 最近邻优化
-
初始化:
- 计算所有垃圾收集点到垃圾处理厂的欧氏距离 c i j c_{ij} cij。
- 按每个点的垃圾量 d i d_i di降序排序。
- 初始化车辆列表,每辆车的剩余载重为 Q Q Q。
-
路径分配:
- 从未分配的垃圾点中,选择垃圾量最大且未被分配的点 i i i。
- 为点 i i i选择最近的车辆 k k k且满足 d i ≤ Q d_i \leq Q di≤Q,将点 i i i分配给车辆 k k k。
- 更新车辆 k k k 的剩余载重 Q k Q_k Qk。
- 如果没有车辆能容纳点 i i i,为点 i i i分配新车辆。
-
路径优化:
- 为每辆车的路径使用最近邻算法,构造从垃圾处理厂出发的最短路径(从当前点选择下一个最近的点)。
- 将路径闭环,返回垃圾处理厂。
-
迭代优化:
- 基于路径总距离,随机调整路径顺序,利用 2-opt 算法(局部路径调整)优化路径。
-
输出结果:
- 每辆车的运输路径。
- 每辆车运输的垃圾量。
- 总行驶距离。
MATLAB实现代码框架
以下为算法的简化实现框架:
matlab
% ============================================
% 基于分批运输与最近邻优化的垃圾运输路径规划
% 问题描述:n个垃圾收集点,每点有固定垃圾量,车辆从处理厂出发收集垃圾后返回,目标是最小化总行驶距离
% ============================================
% 2025-05-24/Ver1
clear; clc; close all;
rng(0);
%% 参数初始化
n = 30; % 垃圾收集点数量
Q = 5; % 车辆最大载重 (吨)
rng(1); % 固定随机数种子
area_size = 100; % 坐标区域大小 (单位: m)
% 随机生成垃圾收集点的坐标和垃圾量
x = rand(n, 1) * area_size;
y = rand(n, 1) * area_size;
d = randi([1, 4], n, 1); % 每个点的垃圾量随机在 [1, 4] 吨
% 垃圾处理厂的坐标 (编号为0)
x = [area_size / 2; x]; % 添加处理厂坐标
y = [area_size / 2; y];
d = [0; d]; % 处理厂不产生垃圾
dist_matrix = pdist2([x, y], [x, y]); % 计算距离矩阵
%% 路径分配与优化
remaining_d = d; % 剩余垃圾量
routes = {}; % 储存每辆车的路径
total_distance = 0; % 总行驶距离
vehicle_id = 1;完整代码的下载链接:https://download.csdn.net/download/callmeup/90897129
运行结果
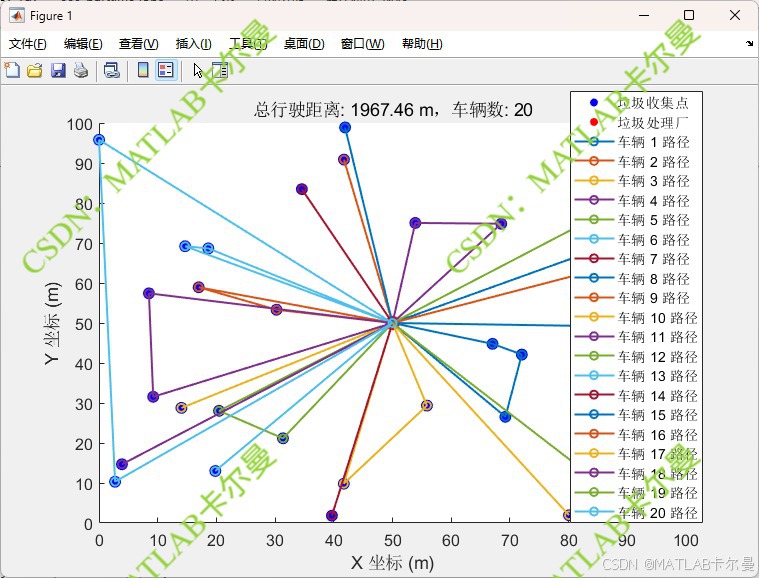
时间复杂度分析
- 路径分配 :
- 每个垃圾点需要计算与所有车辆的距离,复杂度为 O ( n 2 ) O(n^2) O(n2)。
- 路径优化 :
- 路径优化(2-opt)复杂度为 O ( k 2 ) O(k^2) O(k2),其中 k k k是路径上的点数。
- 总复杂度 :
对于 m m m辆车,总复杂度约为 O ( m ⋅ n 2 ) O(m \cdot n^2) O(m⋅n2)。
模型的局限性与改进
局限性
- 未考虑交通因素 :
- 实际行驶过程中可能受到交通拥堵影响,导致路径时间不同。
- 未考虑车辆多样性 :
- 假设所有车辆载重相同,忽略现实中车辆性能的差异。
- 未考虑动态需求 :
- 假设垃圾量固定,未考虑动态变化(如高峰时段)。
改进方向
- 引入时间窗约束 :
- 增加时间窗限制,确保垃圾及时清运。
- 多目标优化 :
- 除最小化总距离外,考虑行驶时间、成本等多目标优化。
- 动态交通建模 :
- 引入交通网络模型,动态调整路径规划。
- 混合车辆模型 :
- 使用不同载重或性能的车辆,优化整体运输效率。
总结
通过数学建模与算法设计,我们成功解决了垃圾运输路径优化问题,最小化了总行驶距离。改进方向可进一步提升模型的适用性与现实性能。
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者