写在前面
关于Games101深度解析参考了很多佬的文章,并且加上了自己的理解。主要感觉games101课程里面还有很多由于时间原因都没讲的很详细,略过了很多,所以我对于课程中困难的知识点进行了更多的步骤思路解释,希望能对正在学习这篇课程的后者提供更清晰的思路。
本文建议配上games101视频以及games101网站中的PDF配合学习https://sites.cs.ucsb.edu/\~lingqi/teaching/games101.html
这一章含有大量线代的几何知识,对于线代的几何理解可以跳到这学习(一步一步看完基本上就没有太大的问题了):https://www.bilibili.com/video/BV1Ys411k7yQ/?spm_id_from=333.337.search-card.all.click&vd_source=93699bcffa78a7a266992d3b23c6dc20
这一章由于知识点都较为简单,所以看起来会很杂,但是后面从第二章开始就开始有章法了。刚开始的数学基础知识就不再提了,我们从线代在图形学的应用开始。
参考文章:
https://zhuanlan.zhihu.com/p/394932478
https://iewug.github.io/book/GAMES101.html#2-3d-transformation
https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
https://caterpillarstudygroup.github.io/GAMES101_mdbook/index.html
向量叉乘的应用
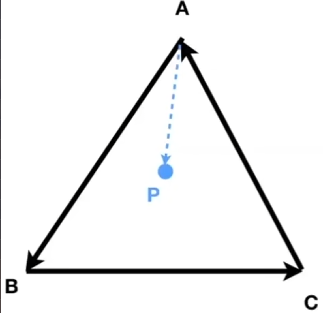
上图中,判断p是否在三角形ABC的内侧,只用将p点与ABC三点相连接,然后再分别叉乘三个边,看结果的符号是否一致,若一致,那么就在内侧,反之亦然。
比如AP叉乘AB,然后BP叉乘BC,然后CP叉乘CA,他们的符号都是一致的,则P就在三角形的里面
指令矩阵在图形学的应用
\[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -x \\ y \end{pmatrix} \]
上面的矩阵做的就是:在二维里面,我们把整个图形以y轴为对称轴做一个对称图形。
那么我们y轴就不用变,把x的数都换个符号就行。上面不止是指令矩阵的角度,线性变换也是这个角度。
几种变换
根据上面的内容我们就可以得到下面的效果
-
缩放矩阵
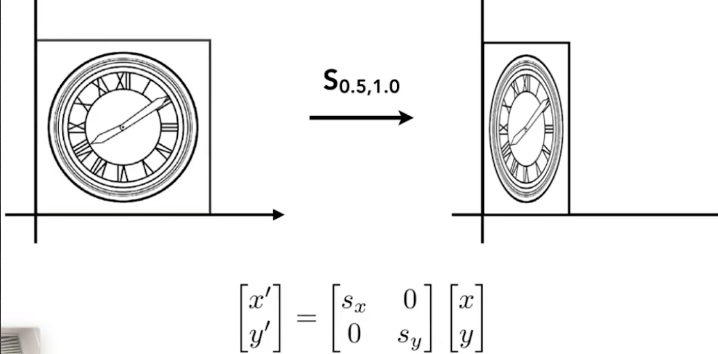
-
拉伸变换
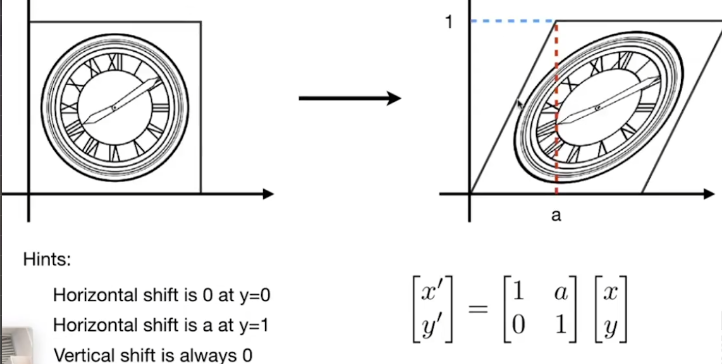
-
旋转变换
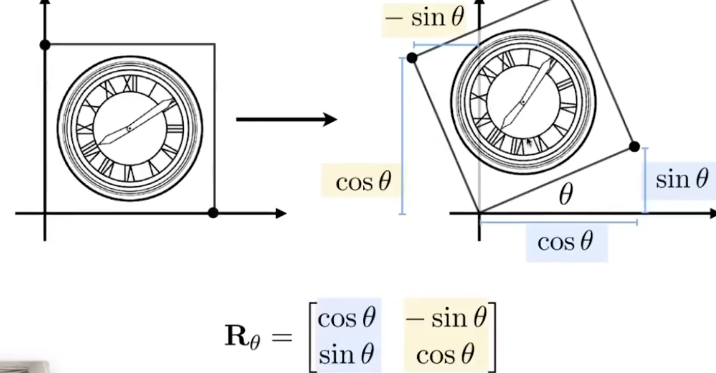
平移变换
我们前面看了这么多变换都是基于原点的变换,但是如果是下面的这个变换(平移)我们该怎么表示呢?
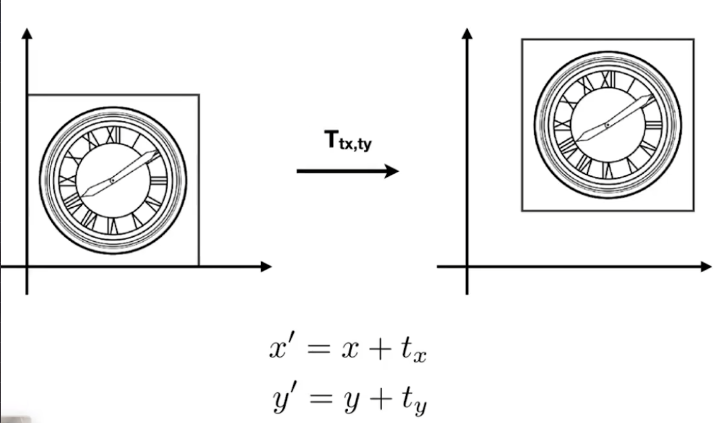
我们这个时候就发现了,我们常规的矩阵往往都只能表示一个向量,但是我们明白,向量平移是不会改变什么的,常规矩阵就是没有办法去表示平移这个动作。
这个时候我们就引入一个新的东西:齐次坐标(homogeneous coordinates)
齐次坐标是用N+1个数来表示N维坐标的一种方式。
要制作二维齐次坐标,我们只需在现有坐标中增加一个额外的变量w,这个w并不代表更高维度的一个坐标,简单说就是表示这里的(x,y)是一个向量或者是一个点。
因此,笛卡尔坐标中的一点,(X,Y)在齐次坐标中就变成了(x,y,w)。在w=1的时候,齐次坐标就是一个点,而w=0的时候,齐次坐标表示的就是一个向量 。而笛卡儿坐标中的X和Y在齐次坐标中的x、y和w则重新表达为(这里把所有的坐标都除了一个\(w\) ,这样\(w\) 的值就必定是1,那就是一个向量)
\[\begin{align} X = x/w\\ Y = y/w\\ \end{align} \]
那怎么应用到实际的平移中呢,就是以下的变换。这样的变换成功表示了每一个平移的点,而且直观的有了一个平移的指令矩阵
\[\begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix} \]
欧氏空间中数学证明:两条平行线可以相交
考虑以下欧氏空间的线性系统。
\[\begin{cases} Ax + By + C = 0 \\ Ax + By + D = 0 \end{cases} \]
而我们知道,由于 \(C \neq D\),所以上述方程没有解。如果 \(C = D\),那么两条线是相同的(重叠的)。
让我们重写投影空间的方程,将 \( x \) 和 \( y \) 分别替换为 \( x/w \),\( y/w \)。
\[\begin{cases} A\frac{x}{w} + B\frac{y}{w} + C = 0 \\ A\frac{x}{w} + B\frac{y}{w} + D = 0 \end{cases} \Rightarrow \begin{cases} Ax + By + Cw = 0 \\ Ax + By + Dw = 0 \end{cases} \]
现在,我们有一个解,(x, y, 0),因为 (C-D)w = 0,所以 w = 0。因此,两条平行线在 (x, y, 0) 处相交。
(x, y, 0) 在几何上代表一条没有起点与终点,也没有长度的射线,它只有方向。
点与向量的加减
- vector + vector = vector
- point - point = vector
- point + vector = vector
- point + point = 两点的中点 (因为\((x_1,y_1,1)\) + \((x_2,y_2,1)\) = \((x_1+x_2,y_1+y_2,2)\) = \((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},1)\)))
仿射变换
\[\begin{pmatrix}x' \\y'\end{pmatrix}=\begin{pmatrix}a & b \\c & d\end{pmatrix}\cdot\begin{pmatrix}x \\y\end{pmatrix}+\begin{pmatrix}t_x \\t_y\end{pmatrix} \]
像这样线性变换之后加上平移量的变换叫做放射变换
所有的放射变换都可以写成齐次坐标的形式
\[\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]
!danger
注意: 在上面的变换中我们能够发现,是先线性变换再进行平移的
- 缩放矩阵
\[\mathbf{S}(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \]
- 旋转矩阵
\[\mathbf{R}(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} \]
- 平移矩阵 :
\[\mathbf{T}(t_x, t_y) = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \]
逆变换
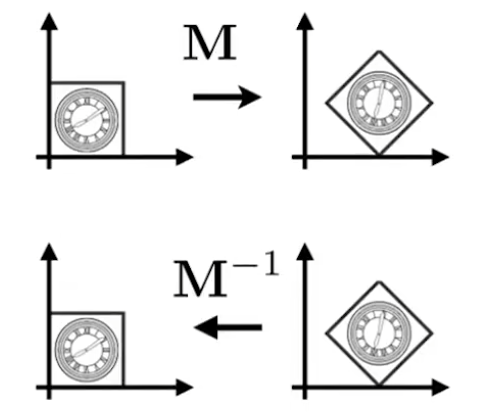
!note
逆变换刚好对应矩阵中:一个矩阵 x 该矩阵的逆矩阵 = 单位矩阵(什么都没做)
值得注意的是,如果旋转负角度,我们就能发现:
!note
旋转矩阵的逆矩阵就是旋转矩阵的转置矩阵:\({R_\alpha}^T={R_\alpha}^{-1}\)
!note\] 如果一个矩阵的逆等于他的转置,那么我们称此矩阵为正交矩阵
\(\mathbf{R}(\alpha) = \begin{pmatrix}\cos \alpha & -\sin \alpha \\\sin \alpha & \cos \alpha \\\end{pmatrix}\) \(\mathbf{R}(-\alpha) = \begin{pmatrix}\cos \alpha & \sin \alpha \\-\sin \alpha & \cos \alpha \\\end{pmatrix} ={R_\alpha}^T={R_\alpha}^{-1}\)
矩阵的乘法没有交换律:变换的顺序会导致结果不同
先平移再旋转如下:
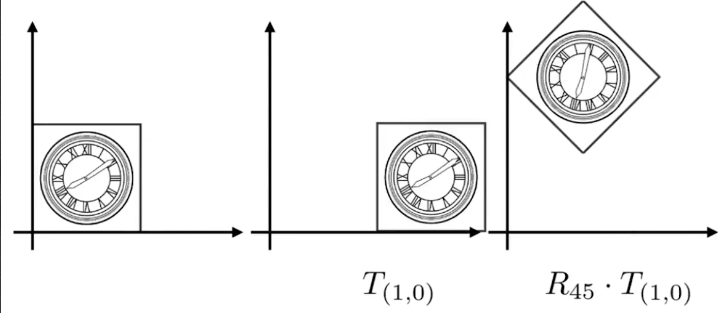
先旋转再平移如下:
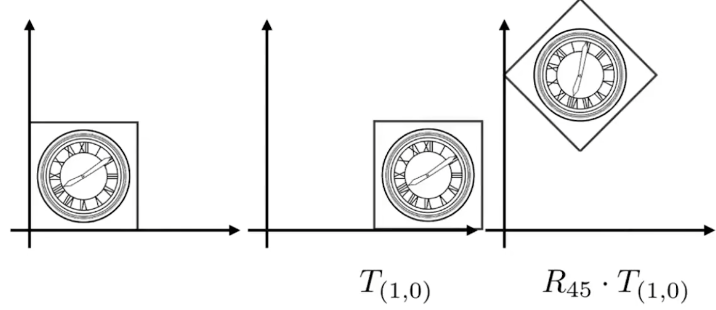
这里就能够体现出两者的变换顺序不同对应着矩阵的乘法没有交换律。
当然,多个线性变换由于有结合律的缘故,我们可以对线性变换先进行线性变换,最后得到一个大的线性变换再对其最开始的向量进行线性变换都行
任意点的旋转
我们前面只知道怎么沿着原点旋转,如果要沿着其他的一个点旋转一个图形,我们就可以先平移到原点,然后进行旋转,最后我们旋转完之后再平移回去是一样的。