目录
[2.1 传统PID控制器](#2.1 传统PID控制器)
[2.2 Q-Learning强化学习原理](#2.2 Q-Learning强化学习原理)
[2.3 Q-Learning与PID控制器的融合架构](#2.3 Q-Learning与PID控制器的融合架构)
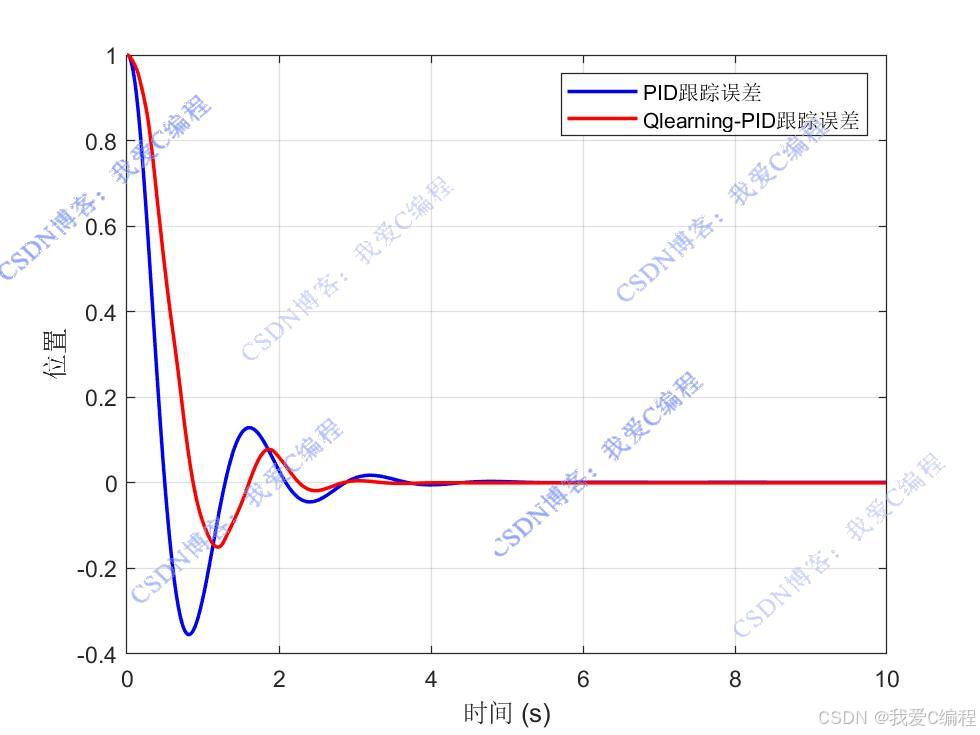
1.算法仿真效果
matlab2024B仿真结果如下**(完整代码运行后无水印)**:
传统PID
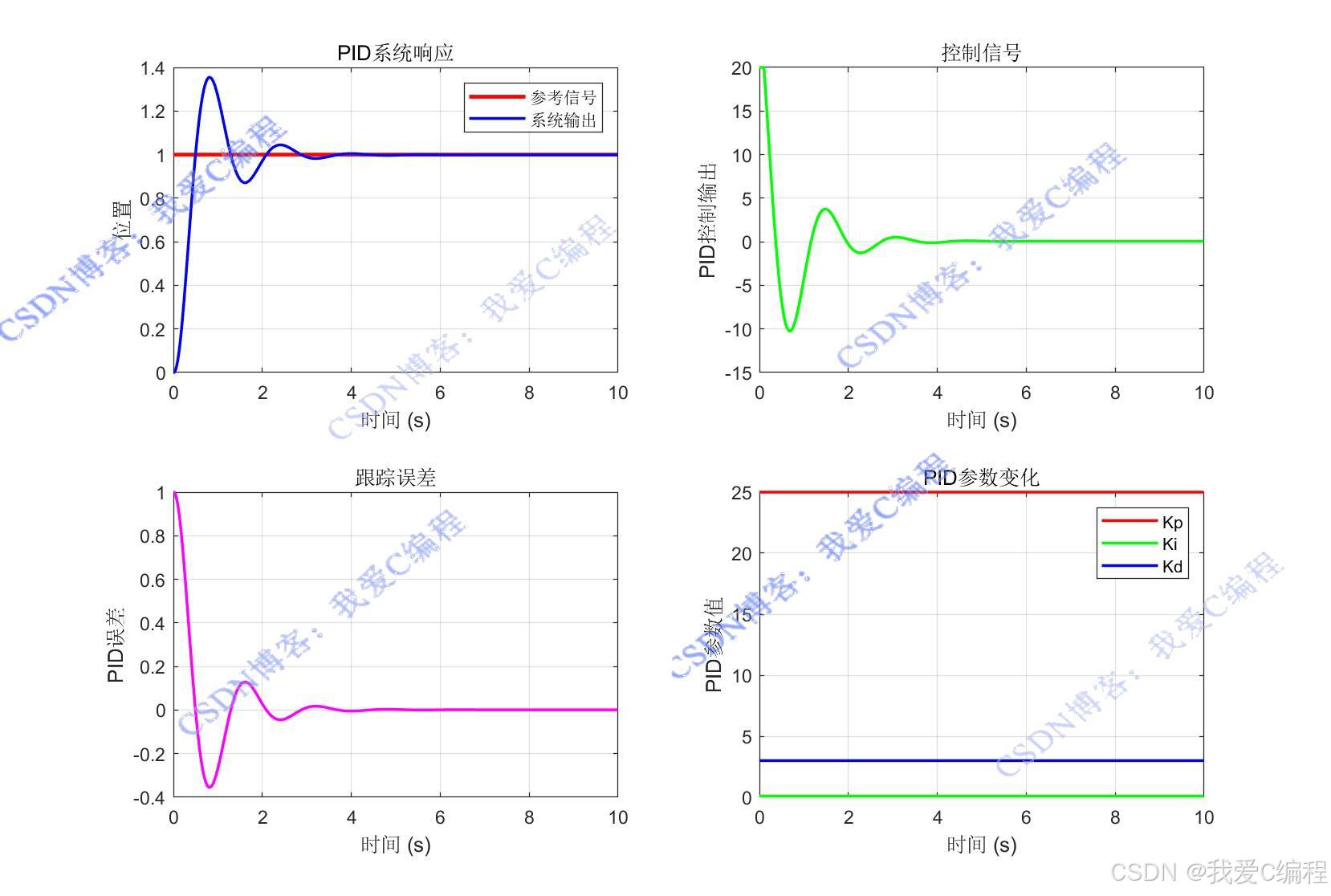
Qlearning-PID
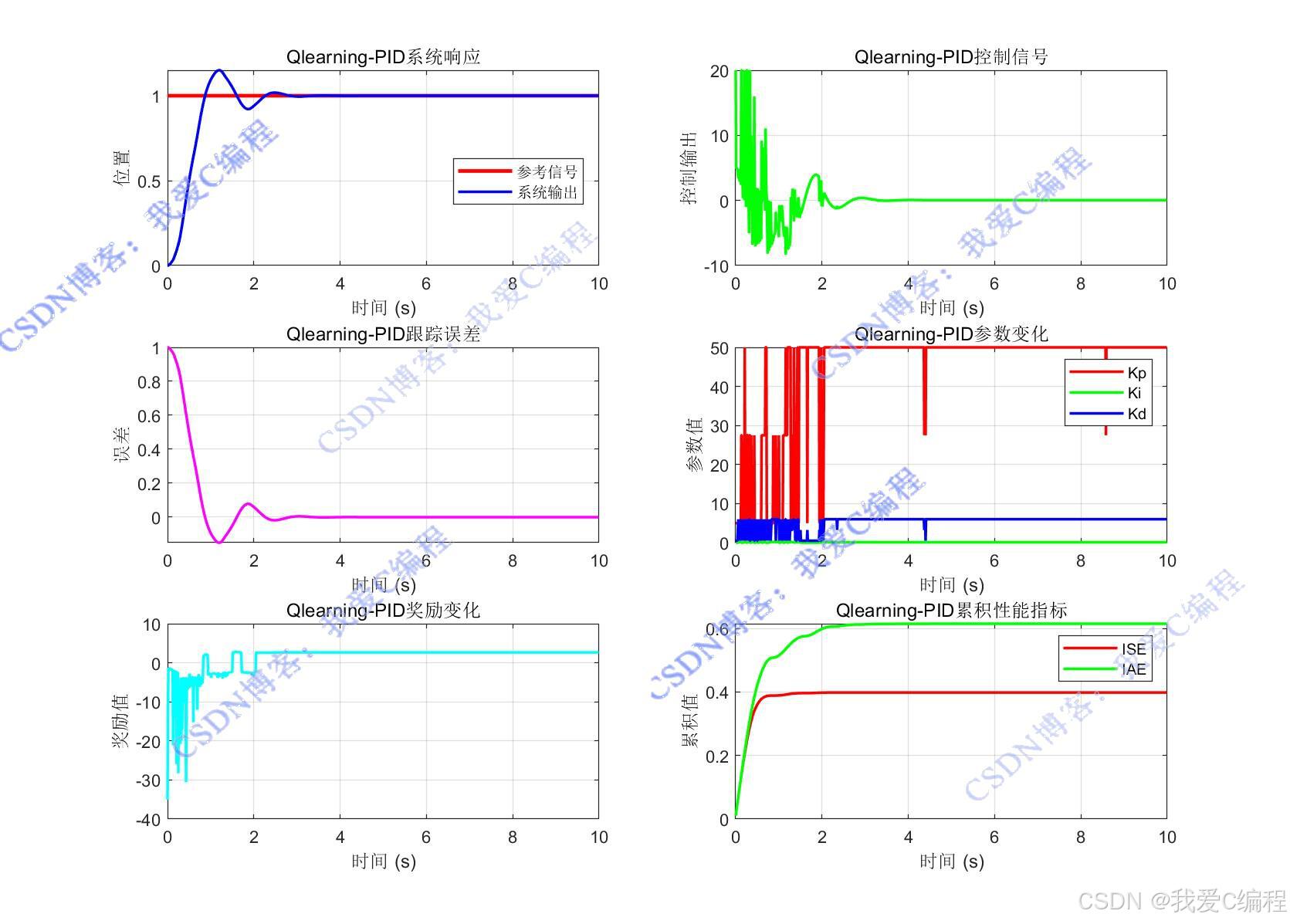
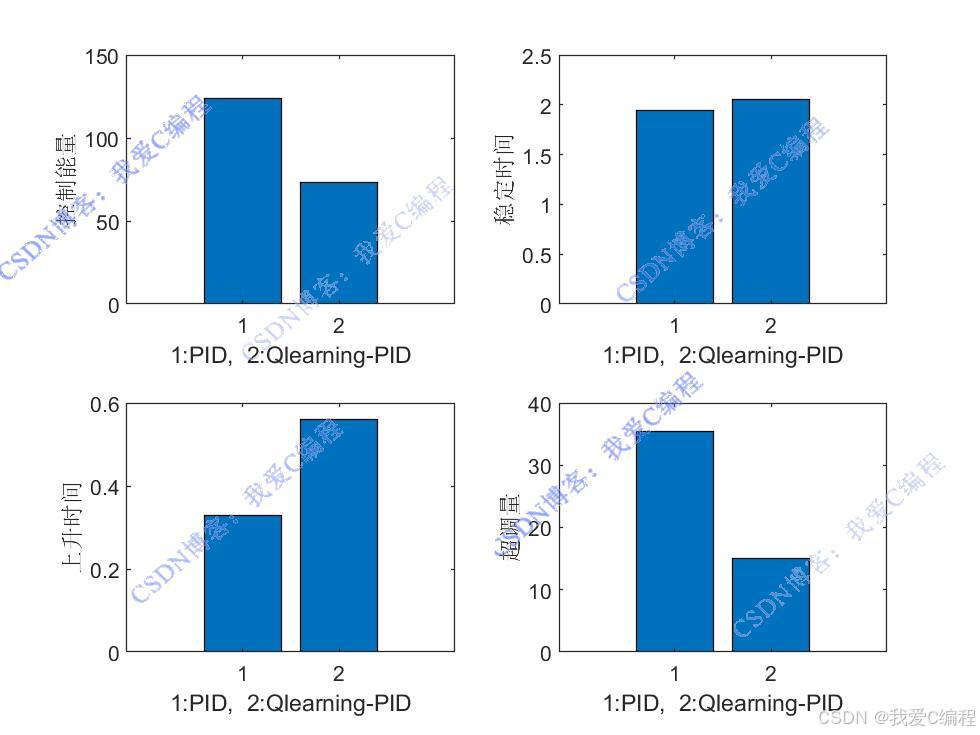
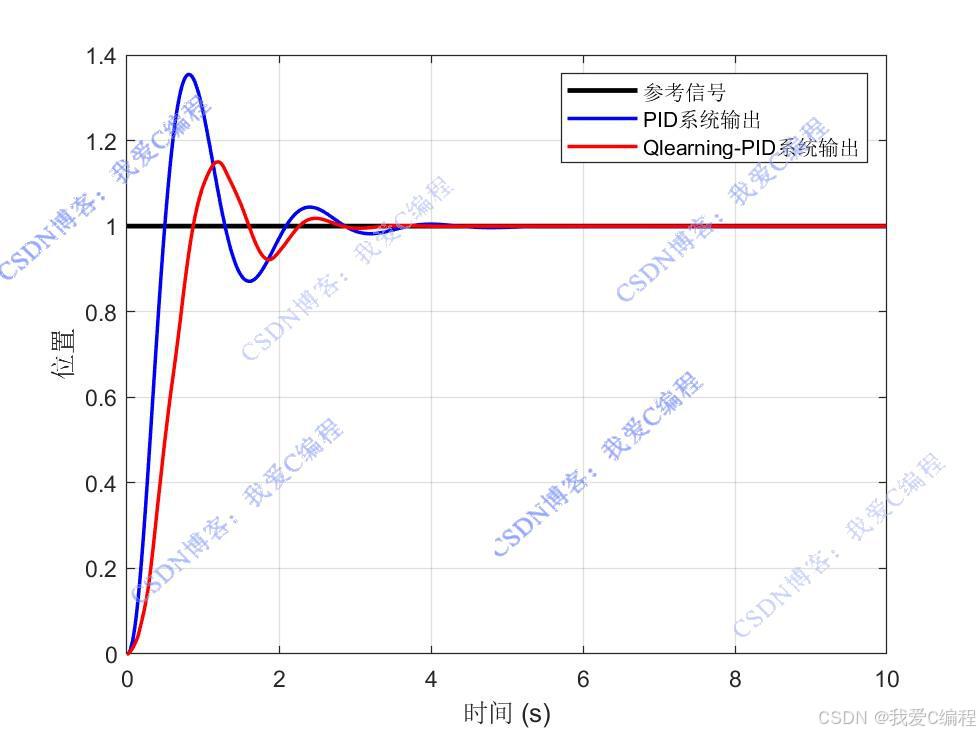
对比:
仿真操作步骤可参考程序配套的操作视频。
2.算法涉及理论知识概要
2.1 传统PID控制器
PID控制器通过比例(P)、积分(I)、微分(D)三个环节的线性组合生成控制量,其核心思想是基于系统当前误差、误差累积和误差变化率进行反馈控制。具体而言:
比例环节(P):即时成比例地反映系统误差,系数Kp越大,响应速度越快,但过大易导致超调。
积分环节(I):消除系统稳态误差,系数Ki决定积分速度,过大可能引发积分饱和。
微分环节(D):预测误差变化趋势,系数Kd可改善系统动态性能,抑制超调,但对噪声敏感。
连续时间域下,PID控制器的输出表达式为:

2.2 Q-Learning强化学习原理
Q-Learning属于时序差分(TD)学习算法,旨在通过迭代更新动作价值函数Q(s,a),找到最优策略π∗(s),使得智能体在状态s下选择动作a时,累积奖励的期望最大化。其核心要素包括:
状态空间(State Space, S):智能体对环境的观测集合,如系统误差、误差变化率等。
动作空间(Action Space, A):智能体可执行的操作集合,如PID参数的调整量。
奖励函数(Reward Function, R):衡量动作优劣的标量反馈,用于引导学习方向。
策略(Policy, π):从状态到动作的映射关系,决定智能体的行为。
2.3 Q-Learning与PID控制器的融合架构
**状态空间定义,**状态空间需选取能反映系统动态特性的关键变量,常见设计包括:

为便于Q表存储和计算,需对连续状态空间进行离散化。常用方法包括:
等距划分:将每个状态变量的取值范围划分为若干等距区间,如将误差e分为[−3,−2,−1,0,1,2,3]七个等级。
模糊化处理:借鉴模糊逻辑,用 "负大""负中""负小""零""正小""正中""正大" 等语言变量划分状态。
**动作空间设计,**动作空间对应PID参数的调整策略,通常有两种形式:

**奖励函数设计,**奖励函数是引导Q-Learning学习的核心,需综合考虑系统性能指标,如:

基于Q-Learning的PID控制器通过强化学习的自适应优化能力,突破了传统PID参数整定的局限性,为复杂系统控制提供了高效解决方案。其核心在于将 PID 参数调整建模为马尔可夫决策过程(MDP),通过状态 - 动作 - 奖励的闭环交互学习最优控制策略。尽管存在计算复杂度高和离散化限制等问题,但其在工业控制、机器人、无人机等领域的成功应用已彰显巨大潜力。随着深度强化学习、连续空间算法的发展,未来该技术有望进一步提升实时性和泛化能力,推动智能控制技术向更广泛的工程场景渗透。
3.MATLAB核心程序
...................................................................................
% 计算稳定时间 (误差小于5%的设定值)
threshold = 0.05 * setpoint;
for i = num_steps:-1:1
if abs(performance_history(i, 1)) > threshold
settling_time = i * Ts;
break;
end
end
% 计算上升时间 (首次达到设定值的10%-90%的时间)
if setpoint ~= 0
rise_start = 0;
rise_end = 0;
for i = 1:num_steps
if position_history(i) >= 0.1*setpoint && rise_start == 0
rise_start = i * Ts;
end
if position_history(i) >= 0.9*setpoint && rise_end == 0
rise_end = i * Ts;
end
end
if rise_start > 0 && rise_end > 0
rise_time = rise_end - rise_start;
end
end
% 计算超调量
if setpoint_type == 'step' & setpoint ~= 0
max_response = max(position_history);
overshoot = 100 * (max_response - setpoint) / setpoint;
end
%% 结果可视化
% 创建图形窗口
figure('Position', [100, 100, 1200, 800]);
% 绘制系统响应
subplot(2, 2, 1);
plot((0:num_steps-1)*Ts, reference_history, 'r-', 'LineWidth', 2);
hold on;
plot((0:num_steps-1)*Ts, position_history, 'b-', 'LineWidth', 1.5);
title('PID系统响应');
xlabel('时间 (s)');
ylabel('位置');
legend('参考信号', '系统输出');
grid on;
% 绘制控制信号
subplot(2, 2, 2);
plot((0:num_steps-1)*Ts, control_history, 'g-', 'LineWidth', 1.5);
title('控制信号');
xlabel('时间 (s)');
ylabel('PID控制输出');
grid on;
% 绘制误差
subplot(2, 2, 3);
plot((0:num_steps-1)*Ts, error_history, 'm-', 'LineWidth', 1.5);
title('跟踪误差');
xlabel('时间 (s)');
ylabel('PID误差');
grid on;
% 绘制PID参数变化
subplot(2, 2, 4);
plot((0:num_steps-1)*Ts, Kp_history, 'r-', 'LineWidth', 1.5);
hold on;
plot((0:num_steps-1)*Ts, Ki_history, 'g-', 'LineWidth', 1.5);
plot((0:num_steps-1)*Ts, Kd_history, 'b-', 'LineWidth', 1.5);
title('PID参数变化');
xlabel('时间 (s)');
ylabel('PID参数值');
legend('Kp', 'Ki', 'Kd');
grid on;
%% 输出性能指标
fprintf('基于PID控制器性能评估:\n');
fprintf('------------------------------------\n');
fprintf('控制能量: %.4f\n', control_effort);
if settling_time > 0
fprintf('稳定时间 (5%%): %.4f s\n', settling_time);
end
if rise_time > 0
fprintf('上升时间 (10%-90%%): %.4f s\n', rise_time);
end
if overshoot > 0
fprintf('超调量: %.2f%%\n', overshoot);
end
fprintf('------------------------------------\n');
fprintf('最终奖励值: %.4f\n', performance_history(end, 7));
fprintf('平均奖励值: %.4f\n', mean(performance_history(:, 7)));
fprintf('探索率: %.4f\n', epsilon);
save R0.mat
0Z_021m4.完整算法代码文件获得
V