大厂面试（三）：JavaScript中两数相加的精度陷阱

引言

在面试的时候，如果面试官问：0.1加0.2等于多少？，阁下会如何应对？

你或许会犹豫片刻，然后自信地回答：0.3。

那么恭喜，你可以提前准备找下一家了...

如果你在浏览器控制台输入console.log(0.1 + 0.2)，你就会发现，你看到的不是熟悉的0.3，而是0.30000000000000004，这个诡异的计算结果背后，其实隐藏着JavaScript深层的秘密。

本文将带你了解JavaScript数值计算的真相，无论你是面试者还是工程师，相信这些知识都会对你有所帮助。

问1：在 JavaScript 中，为什么0.1+0.2 ≠0.3

答案

因为JavaScript 使用 IEEE 754 标准的 64 位浮点数来存储所有数字，这导致计算过程中存在精度丢失 和误差叠加。

解析

1. js中数字的存储方式

   众所周知，在早期的ES5版本中，JavaScript的简单数据类型其实只有五种，即Number、String、Bollean、Undefined、Null。

   其中，能实现计算的只有 Number 类型，而其中所有的数字都以 64 位浮点数的方式进行存储（IEEE 754 标准）

   所谓的IEEE 754 标准，即 1位符号位，11位指数位，52位尾数位，如下图所示：

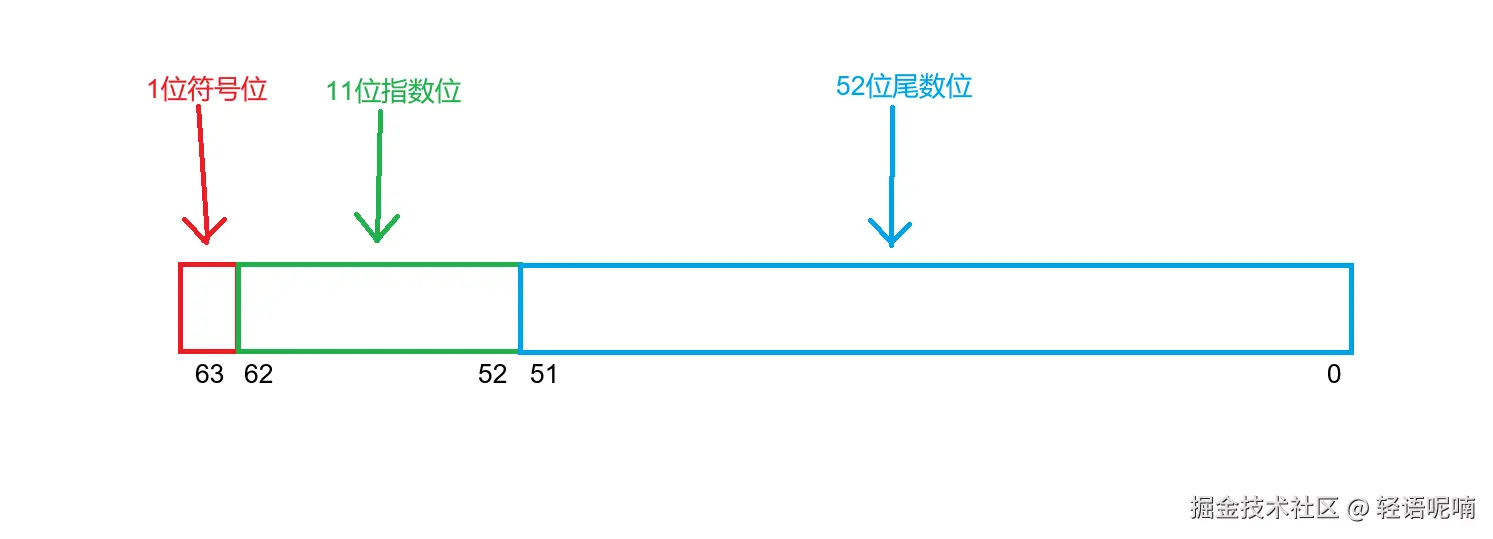
2. 精度丢失原理

   十进制小数转为二进制时会产生无限循环。

   如0.1，其实它长这样：
   0.0001100110011001100110011001100110011001100110011001101

   而0.2 长得也差不多：
   0.0011001100110011001100110011001100110011001100110011010

   在做加法运算时，其实是对二进制数进行相加，比如上面两串数字，它们的运算结果为：
   0.010011001100110011001100110011001100110011001100110100

   把它转换回小数，也就是是0.30000000000000004

   所以，在JavaScript中，0.1 + 0.2 = 0.30000000000000004而不是我们熟悉的0.3。

   当然，这其实不是 JavaScript 的 bug，而是所有遵循 IEEE 754 标准的语言的二进制浮点数固有缺陷。

---

问2：如何使得 0.1 +0.2 等于 0.3 ？**

答案

可以通过使用以下四种方法实现：

方法 1：整数转换法（推荐）

将小数转为整数计算后再转回小数：

function add(a, b) {
  // 获取小数位数
  const aDecimals = a.toString().split('.')[1]?.length || 0;
  const bDecimals = b.toString().split('.')[1]?.length || 0;
  
  // 计算最大精度
  const precision = 10 ** Math.max(aDecimals, bDecimals);
  
  // 转为整数计算
  return (a * precision + b * precision) / precision;
}

console.log(add(0.1, 0.2)); // 0.3

原理：

1. 通过 toString() 将a转换为字符串的形式，然后用 split('.') 将字符串分割成整数部分和小数部分，如果小数点后一位（即索引为1的位置）存在，则计算得到小数的位数，否则则为0。
2. 通过Math.max(aDecimals , bDecimals)得到最大精度，并得到10的该次幂。
3. a和b全部乘以该最大精度化，得到整数，相加后再除以该最大精度变回小数。

✅ 优点 ：无依赖、直观易懂

⚠️ 限制：小数位数超过 5 位时需改用 BigInt (详情可见方法4)

---

方法 2：toFixed() 显示控制

// 显示时控制精度（返回字符串）
console.log((0.1 + 0.2).toFixed(1)); // "0.3"

// 转换为数字（注意可能重新引入误差）
console.log(+(0.1 + 0.2).toFixed(1)); // 0.3

---

方法 3：专业数学库

使用第三方库彻底解决精度问题：

// 使用 decimal.js 库
import { Decimal } from 'decimal.js';

const result = new Decimal(0.1).plus(0.2);
console.log(result.toString()); // "0.3"
console.log(result.toNumber()); // 0.3

---

方法 4：BigInt 终极方案

// 将 0.1+0.2 转为 1+2 计算
const result = (1n + 2n) / 10n; 
console.log(Number(result)); // 0.3

问3：既然小数计算存在问题，那整数的计算呢？

答案

JavaScript中，当整数的大小超过一定限度时，其实也存在精度丢失问题，而安全整数范围是：从 -2⁵³ - 1 到 2⁵³ - 1 ， 即 Number.MIN_SAFE_INTEGER 到 Number.MAX_SAFE_INTEGER

解析

1. 安全整数边界

   从问1 我们得知，JavaScript 使用 64 位浮点数存储数字，其中 52 位用于存储尾数，所以，它实际可表示 53 位（符号位+尾数位）二进制数。

   因此最大安全整数为：
   2⁵³ - 1 = 9007199254740991

   最小安全整数为：
   -2⁵³ - 1 = -9007199254740991

   超出该范围的整数运算会出现精度丢失：

   console.log(9007199254740991 + 1);  // 9007199254740992 ✅
   console.log(9007199254740991 + 2);  // 9007199254740992 ❌ 结果错误！

---

问4：如何实现超安全整数范围的大数相加？

答案

两种主流方案：

方案一：字符串模拟人工计算（通用算法）

function add(num1, num2) {
  let result = '';           // 结果字符串
  let carry = 0;             // 进位值
  let i = num1.length - 1;   // 从个位开始计算
  let j = num2.length - 1;

  while (i >= 0 || j >= 0 || carry > 0) {
    // 获取当前位数字（缺位补0）
    const digit1 = i >= 0 ? parseInt(num1[i]) : 0;
    const digit2 = j >= 0 ? parseInt(num2[j]) : 0;
    
    // 计算当前位总和（含进位）
    const sum = digit1 + digit2 + carry;
    
    // 更新结果和进位
    result = (sum % 10) + result;  // 当前位结果
    carry = Math.floor(sum / 10);  // 进位值
    
    // 移动指针
    i--;
    j--;
  }
  
  return result;
}

// 测试（支持任意长度数字）
console.log(add("12345678901234567890", "98765432109876543210")); 
// 输出："111111111011111111100"，结果正确

算法解析

1. 从右向左逐位计算：模拟人工竖式计算过程

2. 三元表达式处理不同位数 ：digit1 = i >= 0 ? ... : 0

3. 进位机制：

   • sum % 10 获取当前位结果
   • Math.floor(sum / 10) 计算进位值

方案二：使用 ES6 BigInt（终极解决方案）

// 数字末尾加 n 声明 BigInt
const a = 123456789012345678901234567890123456789n;
const b = 1n; 

// 直接计算
console.log(a + b); // 123456789012345678901234567890123456790n

// 字符串转 BigInt
const c = BigInt("123456789012345678901234567890123456789");
console.log(c + 1n); // 同上

关键特性

1. 无位数限制：理论支持无限大整数

2. 类型安全：

   typeof 1n; // "bigint"
   1n === 1;  // false （类型不同）

3. 运算规则：

   • 只能与 BigInt 类型运算
   • 不支持小数（但可通过缩放法实现）

总结：

两大核心问题

1. 小数精度陷阱
   IEEE 754浮点数存储导致：
   0.1 + 0.2 = 0.30000000000000004
2. 整数安全边界
   安全范围：-9007199254740991 到 9007199254740991
   越界计算：9007199254740991 + 2 = 9007199254740992（错误）

四大解决方案

场景	解决方案	代码示例
常规小数计算	整数转换法	(0.1*10 + 0.2*10)/10
超大整数计算	BigInt	12345678901234567890n + 1n
兼容旧环境	字符串算法	addStrings("999","1")
科学计算	decimal.js专业库	new Decimal(0.1).plus(0.2)