说明:这是一个机器学习实战项目(附带数据+代码+文档 ),如需数据+代码+文档 可以直接到文章最后关注获取。


1 . 项目背景
在金融投资领域,风险管理是保障资产安全、实现稳健收益的核心环节。VaR(Value at Risk)和ES(Expected Shortfall)作为衡量市场风险的重要统计指标,广泛应用于金融机构和投资组合管理中。随着金融市场波动加剧,投资者对风险的量化能力提出了更高要求。
本项目旨在利用Python编程语言,基于方差-协方差方法构建投资组合的VaR与ES模型,通过对多资产收益率数据的风险建模,实现对潜在最大损失及其期望损失值的定量分析。该模型不仅能够帮助投资者清晰评估在一定置信水平下的最大可能损失,还能进一步揭示极端风险事件发生时的平均损失程度,为投资决策提供有力支持。该项目具备较强的实用性和可扩展性,适用于金融数据分析、风险管理及量化投资等相关场景。
本项目通过Python基于方差-协方差方法实现投资组合风险管理的VaR与ES模型项目实战。
2 . 数据获取
本次建模数据来源于网络(本项目撰写人整理而成),数据项统计如下:
|------------|--------------|------------|
| 编号 | 变量名称 | 描述 |
| 1 | ts_code | 证券代码 |
| 2 | trade_date | 交易日期 |
| 3 | open | 开盘价 |
| 4 | high | 最高价 |
| 5 | low | 最低价 |
| 6 | close | 收盘价 |
| 7 | pre_close | 昨收价 |
| 8 | change | 涨跌额 |
| 9 | pct_chg | 涨跌幅 |
| 10 | vol | 成交量 |
| 11 | amount | 成交额 |
数据详情如下(部分展示):
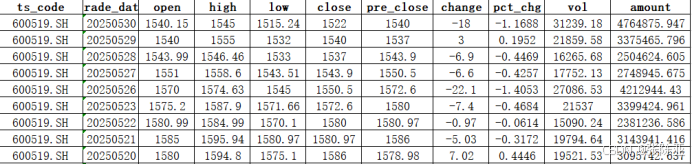
3. 数据预处理
3.1 用P andas 工具查看数据
使用Pandas工具的head()方法查看前五行数据:

关键代码:

3.2 数据缺失查看
使用Pandas工具的info()方法查看数据信息:
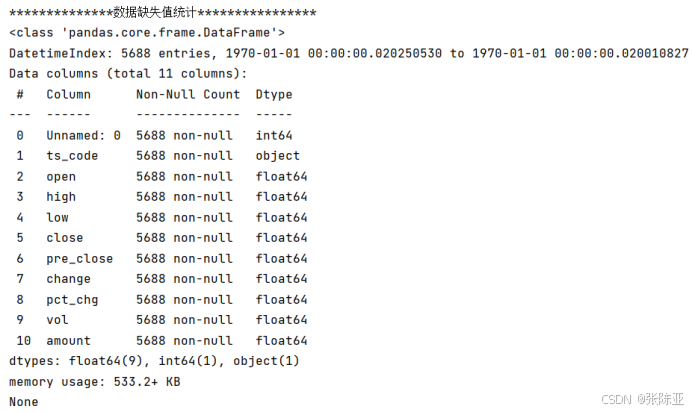
从上图可以看到,总共有10个变量,数据中无缺失值,共5688条数据。
关键代码:

3. 3数据描述性统计
通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。
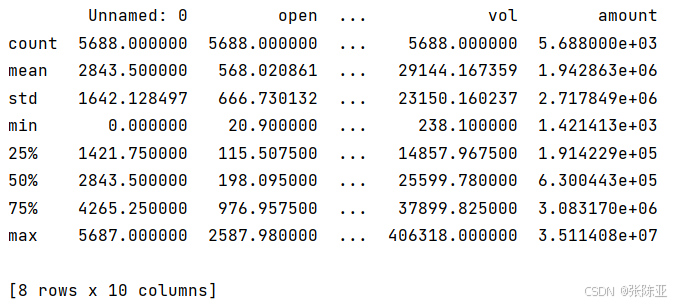
关键代码如下:

4. 探索性数据分析
4 .1 分布直方图
用Matplotlib工具的hist()方法绘制直方图:
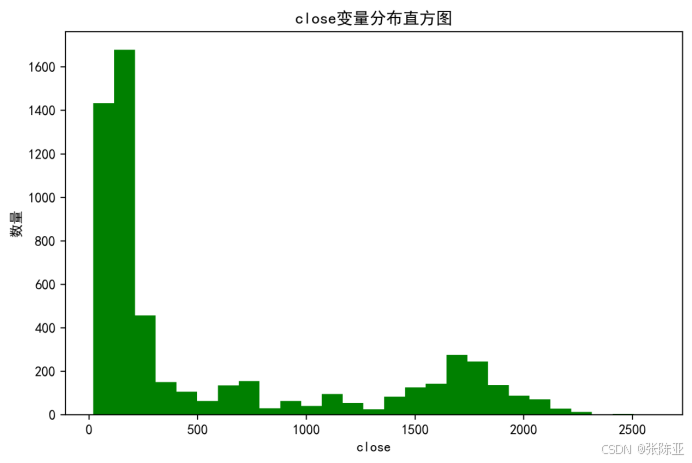
4 .2 相关性分析

从上图中可以看到,数值越大相关性越强,正值是正相关、负值是负相关。
5. 特征工程
5.1 构建日收益率
关键代码如下:

6. 构建VaR与ES模型
主要使用通过Python基于方差-协方差方法实现投资组合风险管理的VaR与ES模型算法。
6. 1 构建模型
|------------|--------------|-------------------------|
| 编号 | 模型名称 | 参数 |
| 1 | VaR模型 | confidence_level = 0.95 |
| 2 | ES模型 | mu |
| 3 | ES模型 | sigma |
| 4 | ES模型 | cl |
7 . 模型评估
7.1 结果分析
VaR和ES模型结果为:

根据方差-协方差方法计算,贵州茅台在95%置信水平下的日度VaR为4.4207%,表示有95%的把握认为每日最大损失不会超过4.42%。Expected Shortfall为-5.6253%,意味着在极端风险事件发生时,平均日损失预计为5.63%。结果表明该股票虽具稳定性,但在小概率情况下仍存在较大下行风险,需引起投资者关注并采取相应风控措施。
7.2 结果可视化

根据图示,贵州茅台股票的日收益率分布呈现出明显的左偏特征,表明其在大多数交易日中收益波动较小,但存在一定的下行风险。通过方差-协方差法计算得出,在95%的置信水平下,VaR为4.4207%,意味着有95%的概率每日最大损失不会超过这一数值;而Expected Shortfall为-5.6253%,表示在极端情况下,平均日损失预计会达到5.63%。这说明尽管茅台股票整体表现较为稳定,但在小概率事件发生时仍面临较大的潜在损失风险。投资者应对此保持警惕,并结合其他风险管理工具进行综合评估和决策,以有效控制投资组合的风险敞口。此外,图中的正态分布拟合曲线与实际收益率分布存在一定差异,提示我们市场可能并不完全符合正态分布假设,需进一步考虑使用更复杂的模型等来提高风险估计的准确性。
8. 结论与展望
综上所述,本文采用了Python基于方差-协方差方法实现投资组合风险管理的VaR与ES模型,最终证明了我们提出的模型效果良好。此模型可用于日常产品的分析。