MoonBit Pearls Vol.01：使用MoonBit编写Pratt解析器

MoonBit Pearls Vol.01：使用MoonBit编写Pratt解析器

上周 MoonBit 社区发起 MoonBit Pearls 高质量文档与示例征集活动，经过精细筛选，本周正式推出"MoonBit Pearls"专栏的首篇入选文章。专栏作为长期知识沉淀平台，持续收录优质文档。我们期待更多开发者参与后续投稿，共同丰富 MoonBit 社区生态。

以下是首篇投稿正文内容，作者通过完整案例，演示了如何用 MoonBit 编写 Pratt 解析器：

在编译过程中，语法分析（也称为解析，Parsing）是一个关键步骤。解析器的主要职责是将Token流转换成抽象语法树（AST）。

本文将介绍一种解析器的实现算法：Pratt解析(Pratt Parsing)， 是自顶向下的算符优先分析法(Top Down Operator Precedence Parsing)，并展示如何用MoonBit来实现它。

为什么用Pratt解析器

几乎每个程序员都不会对中缀表达式感到陌生, 即使是坚定的Lisp/Forth程序员，至少也知道世界上有大半人这样写算术表达式：

而对于编译器(或者解释器)的编写者而言，这样的中缀表达式要比Lisp所用的前缀表达式和Forth使用的后缀表达式难解析一点。例如，使用朴素的手写递归下降解析器来解析就需要多个互相递归的函数，还得在分析表达式语法时消除左递归，这样的代码在运算符增多时变得很不友好。解析器生成工具在这一问题上也不是很令人满意的选项，以一个简单加法和乘法运算表达式的BNF为例：

这看起来并不是很直观，搞不好还得花时间复习一下大学里上过的形式语言课程。

而有些语言如Haskell支持自定义的中缀运算符，这几乎不太可能简单地用某种解析器生成工具解决。

Pratt解析器很好地解决了中缀表达式解析的问题，与此同时，它还很方便扩展支持添加新的运算符(不需要改源码就可以做到！)。它被著名的编译原理书籍《Crafting Interpreters》推荐和递归下降解析器一同使用，rust-analyzer项目中也使用了它。

结合力

Pratt 解析器中用于描述结合性和优先级的概念叫做binding power(结合力)，对于每个中缀运算符而言，其结合力是一对整数 - 左右各一个。如下所示：

而其作用和名字非常符合，数字越大，越能优先获取某个操作数(operand, 这个例子中A B C都是操作数)。

上面的例子展示了具有不同优先级的运算符，而同一运算符的结合性通过一大一小的结合力来表示。

在这个例子中，当解析到B时，由于左边的结合力较大，表达式会变成这样：

接下来让我们看看Pratt解析器在具体执行时如何使用这一概念。

概览与前期准备

Pratt解析器的主体框架大概是这样：

从上文可以看出，它是交替使用递归和循环实现的。这其实对应着两种模式：

• 永远是最左边的表达式在最内层，即"1 + 2 + 3" = "(1 + 2) + 3", 只需要使用循环就能解析
• 永远最右边的表达式在最内层，即"1 + 2 + 3" = "1 + (2 + 3)", 这只使用递归也可以解析

min_bp是一个代表左侧某个还没有解析完毕的运算符结合力的参数。

我们的目标是读入一个token流，并输出一个不需要考虑优先级的前缀表达式：

由于这个过程中可能有各种各样的错误，所以parseExpr的返回类型是Sexpr ! ParseError。

不过在开始编写解析器之前，我们还需要对字符串进行分割，得到一个简单的Token流。

这个token流需要实现两个方法：peek() pop()

peek()方法能获取token流中的第一个token，对状态无改变，换言之它是无副作用的，只是偷看一眼将要处理的内容。对于空token流，它返回Eof。

pop()在peek()的基础上消耗一个token。

tokenize函数负责将一个字符串解析成token流。

最后我们还需要一个计算运算符结合力的函数，这可以用简单的match实现。在实际操作中为了便于添加新运算符，应该使用某种键值对容器。

解析器实现

首先取出第一个token并赋值给变量lhs(left hand side的缩写，表示左侧参数)。

• 如果它是操作数，就存储下来
• 如果是左括号，则递归解析出第一个表达式，然后消耗掉一个成对的括号。
• 其他结果都说明解析出了问题，抛出错误

接着我们试着看一眼第一个运算符：

• 假如此时结果是Eof，那并不能算失败，一个操作数也可以当成是完整的表达式，直接跳出循环
• 结果是运算符, 正常返回
• 结果是右括号，跳出循环
• 其他结果则返回ParseError

接下来我们需要决定lhs归属于哪个操作符了，这里就要用到min_bp这个参数，它代表左边最近的一个尚未完成解析的操作符的结合力，其初始值为0(没有任何操作符在左边争抢第一个操作数)。不过，此处我们要先做个判断，就是运算符是不是括号 - 假如是括号，说明当前是在解析一个括号里的表达式，也应该跳出循环直接结束。这也是使用peek方法的原因之一，因为我们无法确定到底要不要在这里就消耗掉这个运算符。

在计算好当前运算符op的结合力之后，首先将左侧结合力l_bp和min_bp进行比较：

• l_bp小于min_bp，马上break，这样就会将lhs返回给上层还等着右侧参数的运算符
• 否则用pop方法消耗掉当前操作符，并且递归调用parseExpr获取右侧参数，只是第二个参数使用当前操作符的右结合力r_bp。解析成功之后将结果赋值给lhs，继续循环

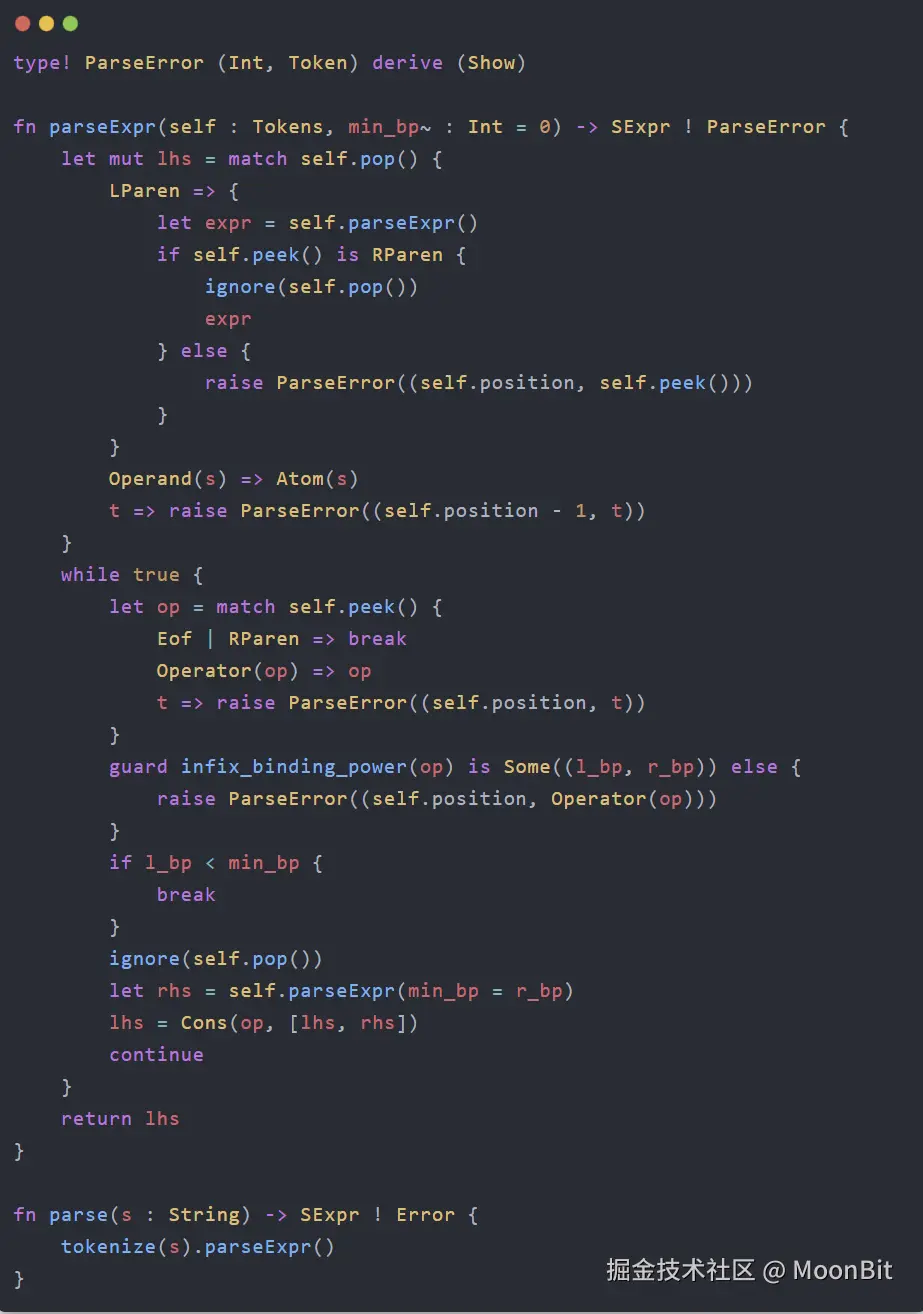
现在我们获得了一个可扩展的四则运算表达式解析器，可以在下面测试块中添加更多的例子来验证其正确性。

不过，pratt parser的能力不止于此，它还可以解析前缀运算符(例如按位取反!n)、数组索引运算符arr[i]乃至于三目运算符c ? e1 : e2。关于这方面更详细的解析请见Simple but Powerful Pratt Parsing, 这篇博客的作者在著名的程序分析工具rust-analyzer中实现了一个工业级的pratt parser。