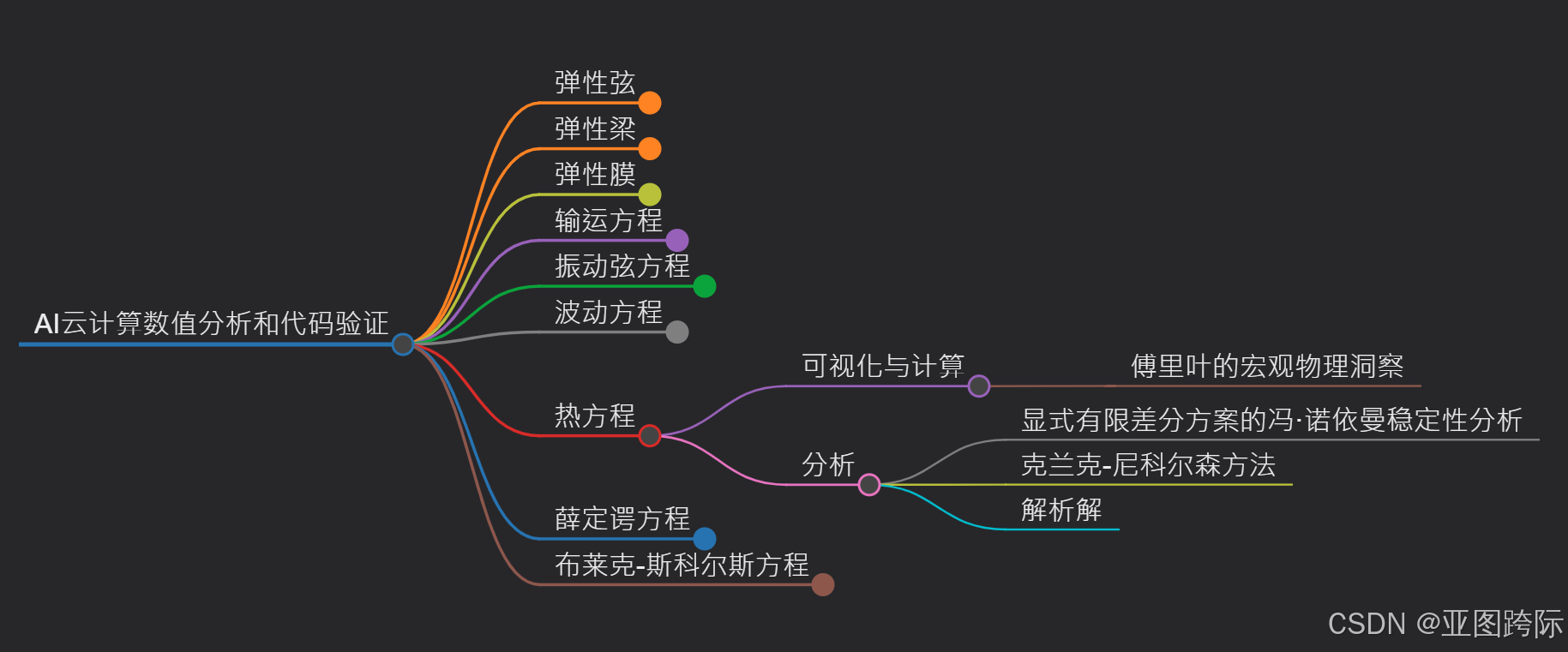
热方程是一个基础的偏微分方程 ,它模拟热量扩散 ,广泛应用于材料科学、工程学、环境研究和理论物理 等多个科学及工程领域。它的重要性体现在其数学表述 、解析和数值可解性 、热源建模能力 以及对复杂多维介质的适应性。
热方程是一个基本的偏微分方程 (PDE),它模拟热量如何随时间在介质中扩散。其应用和重要体现涵盖了各种科学和工程领域,详情如下。
热方程的应用
1. 材料科学
热方程对于理解和预测材料中的温度分布至关重要。它有助于设计具有特定热性能的材料,并分析复合材料及其他复杂材料中的热传递。这种建模对于优化制造和材料工程中的热管理至关重要。
2. 工程学
在工程学中,热方程指导热交换器、电子冷却系统和隔热材料的设计与优化。它使工程师能够预测温度分布和热通量,确保设备和结构中的有效热管理。
3. 环境科学
热方程模拟土壤和地下环境中的热行为。它被用于研究地热能系统、与气候相关的土壤温度变化以及水流对地下热传递的影响。例如,它有助于分析雨水循环如何影响土壤中的季节性温度传播,这对于环境和农业应用非常重要。
4. 物理学和数学
除了实际应用,热方程还是纯数学和理论物理学的基石。它作为抛物型偏微分方程的典型,并与谱几何和几何流(如在证明庞加莱猜想中发挥作用的 Ricci 流)相关联。它还通过布莱克-斯科尔斯方程等变体与布朗运动等随机过程和金融数学联系起来。
5. 其他科学领域
- 量子力学: 薛定谔方程可被视为具有虚时间的热方程。
- 图像分析: 热方程用于平滑图像、减少像素化和检测边缘。
- 流体动力学: 它有助于使用人工粘度方法建立冲击波模型。
热方程的重要体现
-
数学公式:
热方程通常写作:
∂ u ∂ t = α ∇ 2 u , \frac{\partial u}{\partial t}=\alpha \nabla^2 u, ∂t∂u=α∇2u,
其中 u u u 是温度, t t t 是时间, α α α 是热扩散系数, ∇ 2 \nabla^2 ∇2 是表示空间变化的拉普拉斯算子。
-
解析解和数值解:
对于简单的几何形状和边界条件,存在精确解,通常通过傅里叶级数或特征函数展开表示。对于复杂问题,有限差分法等数值方法通过离散化空间和时间来近似求解,从而实现实际工程应用。
-
热源建模:
非齐次热方程包含热源或热沉,允许对具有内部加热的系统进行建模,例如带有加热器的房间或核反应堆。
-
扩展到多维和复杂介质:
热方程适用于一维、二维或三维,并且可以适应各向异性或非均匀材料,从而实现对各种情况下热传导的真实模拟。
总而言之,热方程提供了一个数学框架,对于建模和理解跨许多学科的热传递至关重要。它的解为热系统设计、环境过程分析以及数学和物理学的基础研究提供了信息,使其成为一个重要且广泛应用的模型。
云计算为热方程的可视化和分析提供了强大的平台,它能够应用傅里叶的宏观物理洞察,通过冯·诺依曼稳定性分析评估数值稳定性,实现克朗克-尼科尔森方法,并与解析解进行比较。