文章目录
第一题
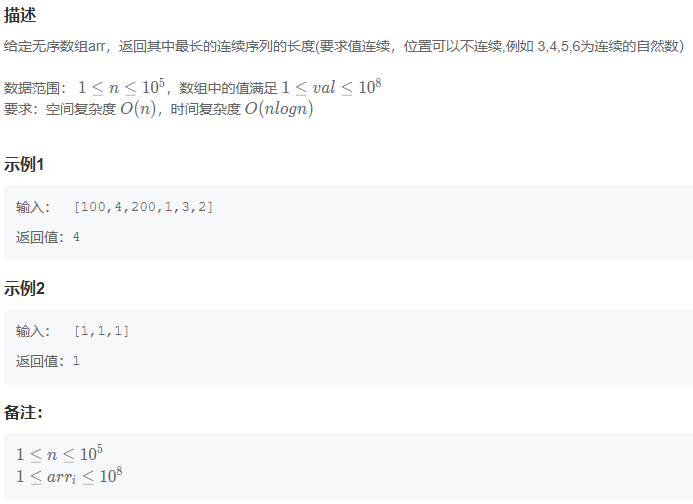
题目
思路
-
最小公倍数等于 = 两数之积除以最大公约数
-
求最大公约数的方法
- 辗转相除法:
先将两个数进行模运算,即a%b
当a%b == 0,直接返回b,b是最大公约数
当a%b != 0,则进行辗转相除,a = b和b = a % b
cppint gcd(int a, int b) { if(a%b == 0) return b; else return gcd(b,a%b); }- 辗转相减法:
不相等时,大的那个赋值为大 - 小,直到相等为止
cppint fun(int a, int b) { while(a != b) { if(a > b) a = a - b; if(b > a) b = b - a; } return a; } - 辗转相除法:
代码
第二题
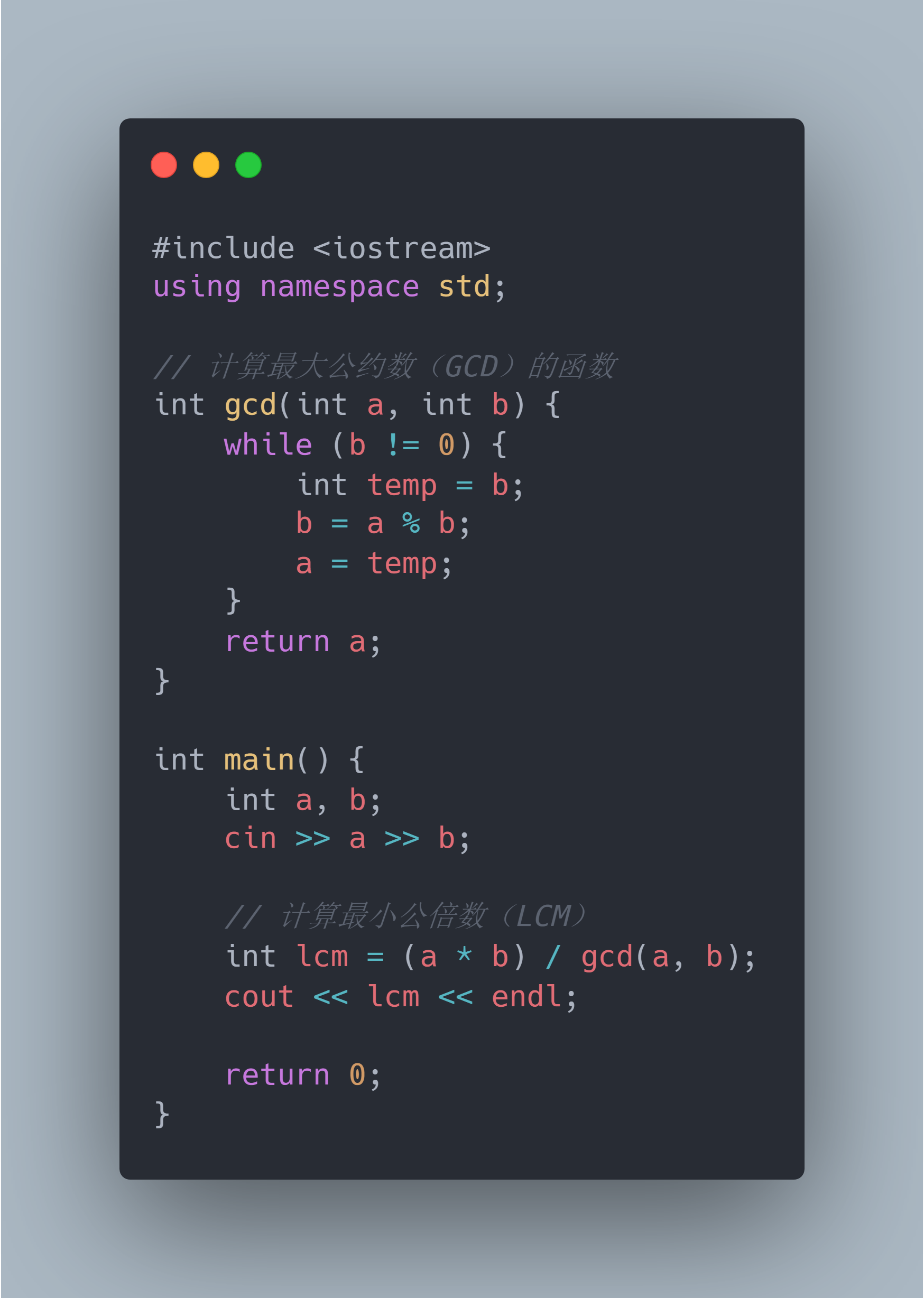
题目:
思路
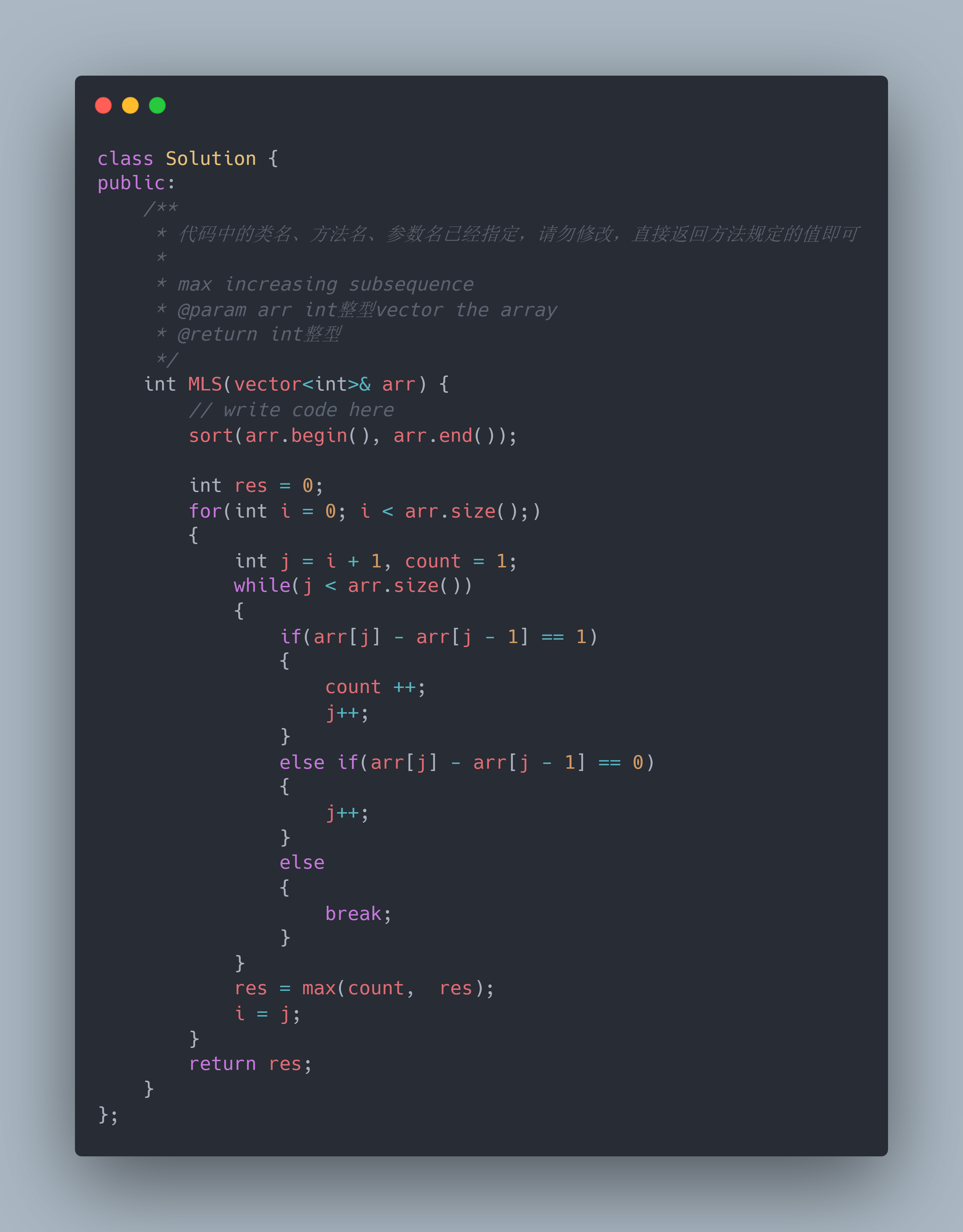
排序 + 模拟
- 排序
- 使用外层循环控制遍历的起始位置 i,对于每个起始位置 i,初始化计数器 count 为 1
- 内层循环从i+1开始遍历
- 如果当前元素比前一个元素大 1,表示连续递增
- 如果当前元素与前一个元素相等,表示重复元素,跳过该元素继续检查下一个
- 如果当前元素与前一个元素的差大于 1,表示连续递增序列中断,退出
代码
第三题
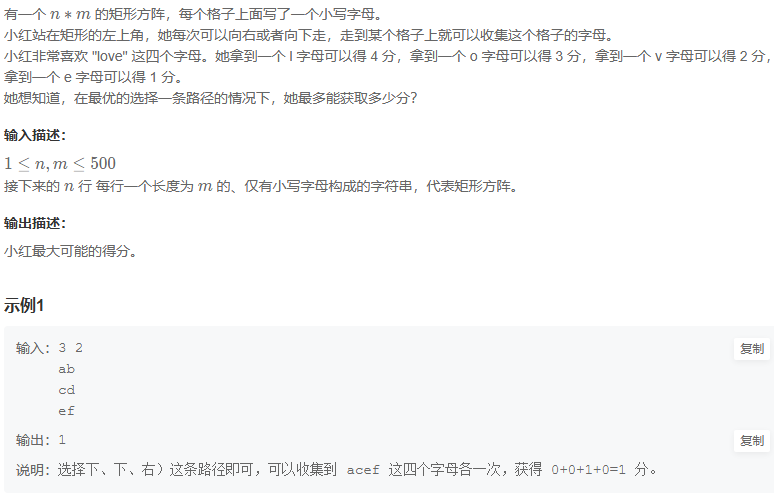
题目:
思路
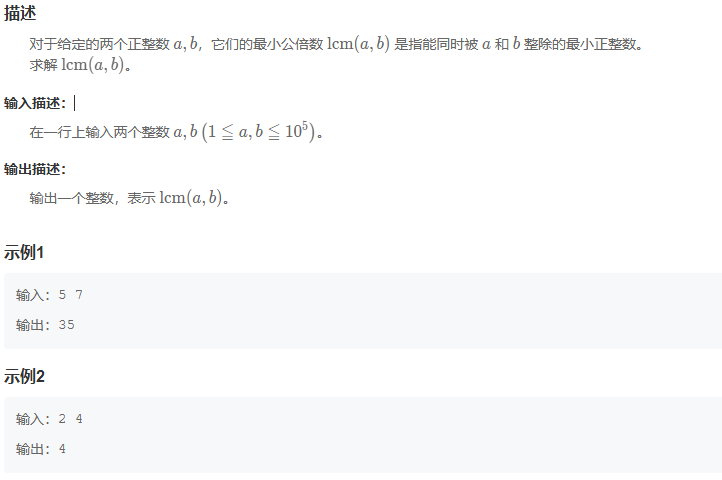
动态规划:
dp[i][j]表示从起点(1,1)到达网格中第i行第j列位置时的最大得分
dp[i][j]只能从上方和左边来;所以,转移方程为:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + t;
代码