代码随想录算法训练营第五十三天任务
- [卡码网97. 小明逛公园(Floyd 算法)](#卡码网97. 小明逛公园(Floyd 算法))
- [卡码网127. 骑士的攻击(A * 算法)](#卡码网127. 骑士的攻击(A * 算法))
- 最短路算法总结
- 图论总结
卡码网97. 小明逛公园(Floyd 算法)
Floyd算法:用于求解图中所有顶点对之间最短路径的动态规划算法
Floyd 算法的核心为:"借助中间节点,不断更新任意两点间的最短路径"。
可以想象成:要找从城市 A 到城市 B 的最短路线,一开始只知道直接走的距离;然后尝试 "绕路"------ 先从 A 到中间城市 K,再从 K 到 B,如果这条绕路的距离比直接走更短,就更新 A 到 B 的最短距离。Floyd 算法会遍历所有可能的中间节点 K,对每一对顶点 (i,j) 都做这样的 "绕路验证",最终得到所有顶点对的最短路径。
借助动规五部曲来分析:
- 确定dp数组以及下标的含义
dp[i][j][k]:表示节点 i 到 节点 j 以 [1...k] 集合中的一个节点为中间节点的最短距离 - 确定递推公式
不经过节点 k:dp[i][j][k-1]
经过节点 k:dp[i][k][k-1] + dp[k][j][k-1]
最短距离:dp[i][j][k] = min(dp[i][j][k-1], dp[i][k][k-1] + dp[k][j][k-1]) - dp数组如何初始化
由递推公式可知,由k-1推导而来,根据边的连接关系,dp[i][j][0] = value; - 确定遍历顺序
k 在最外层
分析见这篇👉思路,很详细 - 举例推导dp数组
层层打印分析
cpp
// 基于三维数组的Floyd算法
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<vector<int>>> grid(n+1, vector<vector<int>>(n+1, vector<int>(n+1, 10001)));
for(int i = 0; i < m; ++i) {
int u, v, w;
cin >> u >> v >> w;
grid[u][v][0] = w;
grid[v][u][0] = w;
}
// floyd算法
for(int k = 1; k <= n; ++k) {
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
grid[i][j][k] = min(grid[i][j][k-1], grid[i][k][k-1] + grid[k][j][k-1]);
}
}
}
int q, start, end;
cin >> q;
// 输出结果
for (int i = 0; i < q; ++i) {
cin >> start >> end;
if (grid[start][end][n] != 10001) {
cout << grid[start][end][n] << endl;
} else {
cout << -1 << endl;
}
}
return 0;
}时间复杂度: O(n3)
空间复杂度:O(n3)
解法二:优化:使用滚动数组
cpp
// 基于二维数组的Floyd算法
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n+1, vector<int>(n+1, 10001));
for(int i = 0; i < m; ++i) {
int u, v, w;
cin >> u >> v >> w;
grid[u][v] = w;
grid[v][u] = w;
}
// floyd算法
for(int k = 1; k <= n; ++k) {
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
}
}
}
int q, start, end;
cin >> q;
// 输出结果
for (int i = 0; i < q; ++i) {
cin >> start >> end;
if (grid[start][end] != 10001) {
cout << grid[start][end] << endl;
} else {
cout << -1 << endl;
}
}
return 0;
}解法三:dijkstra解法
cpp
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int n; // 节点数
void dijkstra(const vector<vector<int>>& graph, vector<int>& minDist) {
vector<bool> isVisited(n+1, false); // 标记访问
for(int i = 1; i <= n; ++i) {
int minVal = INT_MAX;
int cur = -1;
// 1. 找到距离起始节点最近的未访问节点。
for(int j = 1; j <= n; ++j) {
if (!isVisited[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
if (cur == -1) break; // 如果没有可访问的节点(所有节点都不可达),提前退出
// 2. 标记该节点已访问。
isVisited[cur] = true;
// 3. 更新未访问节点到起始节点的距离
for (int j = 1; j <= n; ++j) {
if (!isVisited[j] && graph[cur][j] != INT_MAX && minDist[cur] + graph[cur][j] < minDist[j]) { // graph[cur][j] == INT_MAX, cur和j没连接
minDist[j] = minDist[cur] + graph[cur][j];
}
}
}
}
int main() {
int m; // 边数
cin >> n >> m;
vector<vector<int>> graph(n+1, vector<int>(n+1, INT_MAX));
// 初始化自身到自身的距离为0
for (int i = 1; i <= n; ++i) {
graph[i][i] = 0;
}
for (int i = 0; i < m; ++i) {
int s, e, v;
cin >> s >> e >> v;
graph[s][e] = v;
graph[e][s] = v;
}
int q, start, end;
cin >> q;
for (int i = 0; i < q; ++i) {
cin >> start >> end;
vector<int> minDist(n+1, INT_MAX); // start到任一节点的最短距离
minDist[start] = 0;
dijkstra(graph, minDist);
if (minDist[end] != INT_MAX) {
cout << minDist[end] << endl;
} else {
cout << -1 << endl;
}
}
return 0;
}卡码网127. 骑士的攻击(A * 算法)

A* 算法是改进版的广搜,使搜索向目标的方向搜索。
A * 算法是一种启发式搜索算法,核心是结合 "从起点到当前节点的真实代价" 和 "当前节点到终点的预估代价",快速找到从起点到终点的最短路径,广泛应用于路径规划(如游戏寻路、地图导航)等场景。
启发函数:起点达到目前遍历节点的距离g + 目前遍历的节点到达终点的距离h = 起点到达终点的距离f。
与广搜的代码类似,A*用优先队列来存储遍历的节点,按照 f 的大小来排序,优先取最小的值来搜索。
cpp
#include <iostream>
#include <vector>
#include <queue>
#include <cstring> // memset函数
using namespace std;
int b1, b2; // 终点坐标
int dir[8][2] = {2, 1, -2, 1, 1, 2, -1, 2, 2, -1, 1, -2, -1, -2, -2, -1}; // 骑士可走的8个方向
int moves[1001][1001]; // 记录路径长度
struct Knight{
int x, y, g, h, f;
// priority_queue需要对元素进行比较,会调用operator< 需调用const成员函数
bool operator<(const Knight& k) const{ // 重载运算符
return k.f < f;
}
};
int Heuristic(const Knight& k) {
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2);
}
priority_queue<Knight> que;
void Astar(const Knight& k) {
Knight cur, next;
que.push(k);
while(!que.empty()) {
cur = que.top();
que.pop();
if (cur.x == b1 && cur.y == b2) break;
for (int i = 0; i < 8; ++i) {
next.x = cur.x + dir[i][0];
next.y = cur.y + dir[i][1];
if (next.x < 1 || next.y < 1 || next.x > 1000 || next.y > 1000) continue;
if (!moves[next.x][next.y]) {
moves[next.x][next.y] = moves[cur.x][cur.y] + 1;
next.g = cur.g + 5; // 起点到当前点的真实距离 5 = 1 * 1 + 2 * 2 ("日"字的对角顶点距离)
next.h = Heuristic(next); // 当前点到终点的预估距离
next.f = next.g + next.h;
que.push(next);
}
}
}
}
int main() {
int n;
cin >> n;
while(n--) {
int a1, a2;
cin >> a1 >> a2 >> b1 >> b2;
memset(moves, 0, sizeof(moves));
Knight start;
start.x = a1;
start.y = a2;
start.g = 0;
start.h = Heuristic(start);
start.f = start.g + start.h;
Astar(start);
while(!que.empty()) que.pop(); // 每轮计算完需要将队列清空
cout << moves[b1][b2] << endl;
}
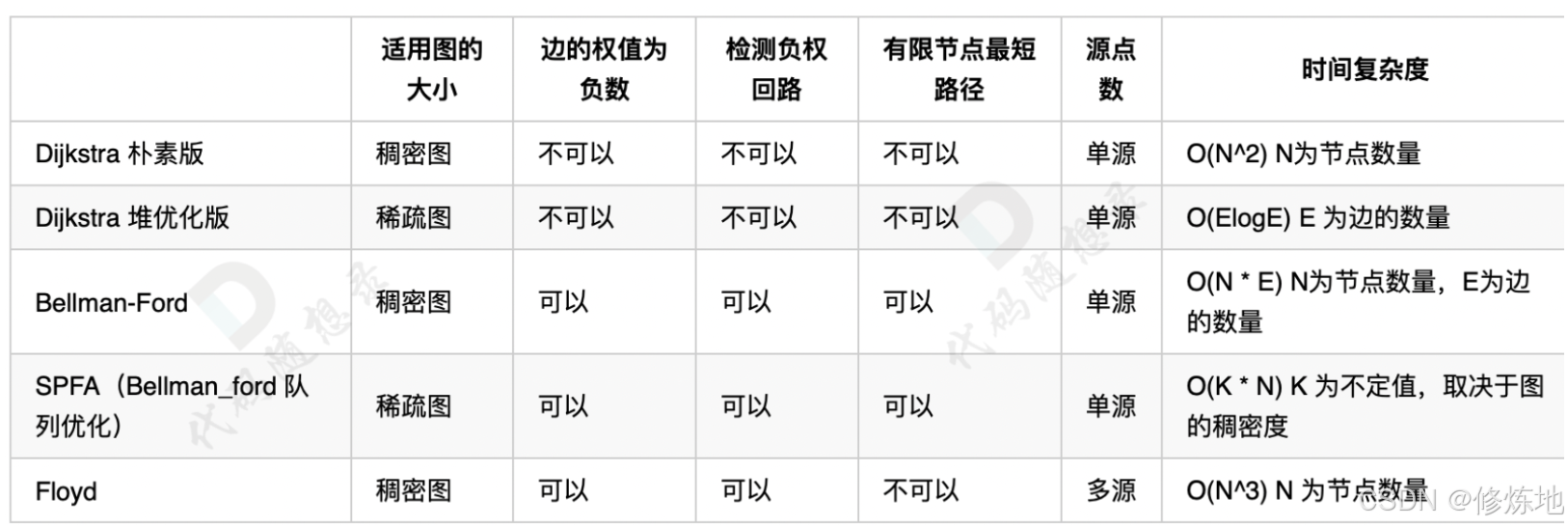
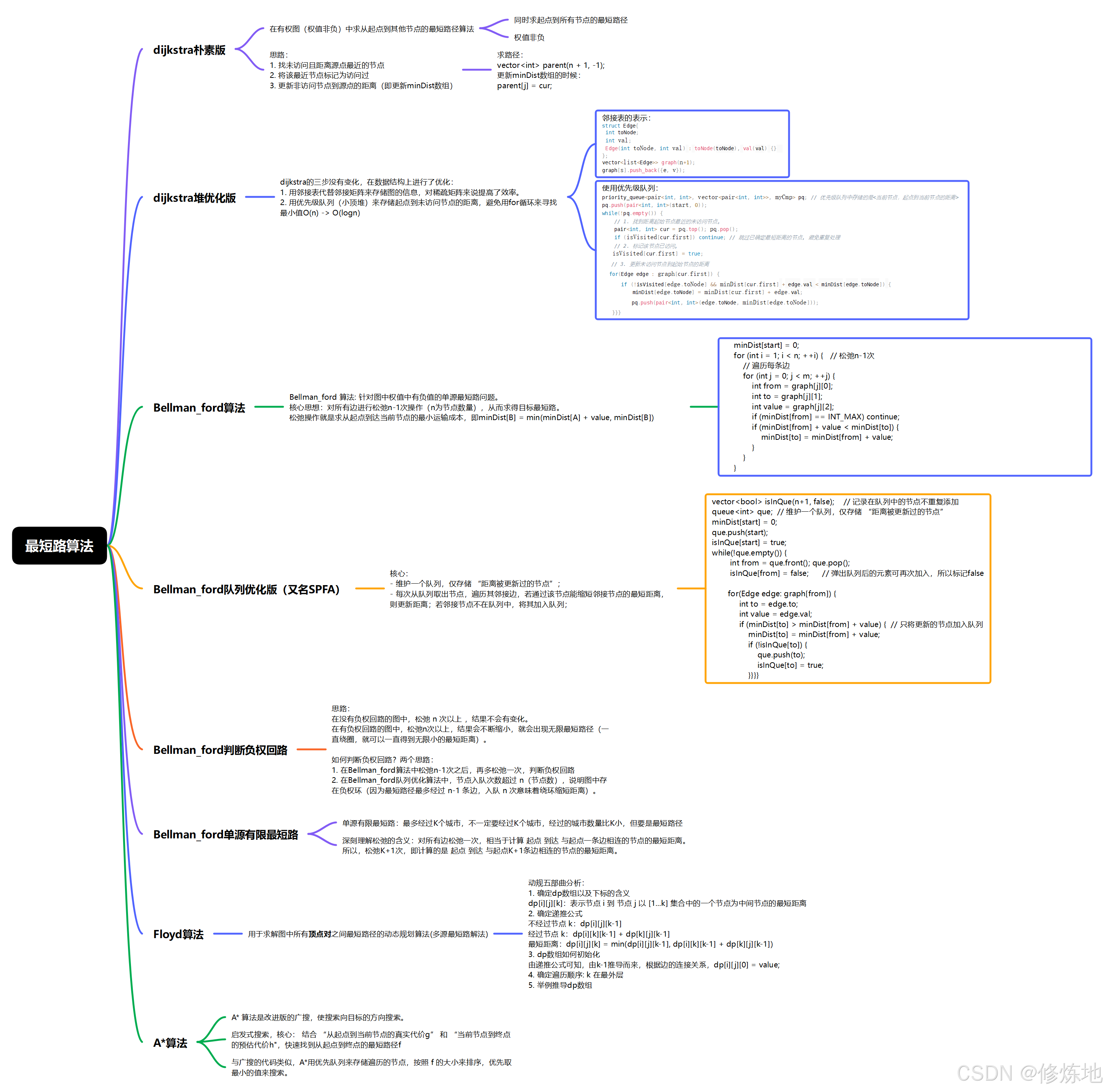
}最短路算法总结
图论总结
深搜:一个方向搜,不到黄河不回头
广搜:一圈一圈地搜索。
并查集:将两个元素添加到一个集合中、判断两个元素在不在同一个集合。
最小生成树:prim算法(三步曲,维护一个minDist数组)、Kruskal算法(并查集)
拓扑排序:把有向图转换为线性的排序(依赖关系),方法是找到入度为0的元素,加入结果集;把入度为0的元素从图中删除。
最短路算法:dijkstra、Bellman_ford、SPFA、Floyd、A*

