《通信原理》学习笔记——第三章

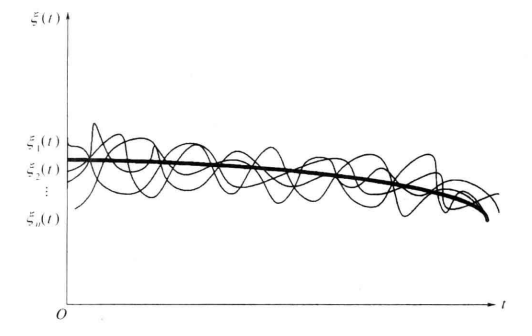
测试结果的每一个记录，即图中的一个波形，都是一个确定的时间函数 xi (t ) ，它称为样本函数 (Sample function) 或随机过程的一次实现 (realization)。全部样本函数构成的总体 { x 1( t ), x 2( t ),⋯, xn ( t )} 就是一个随机过程，记作 ξ ( t )

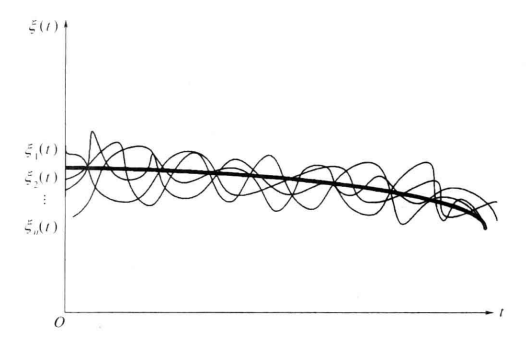
在任一给定时刻 t 1 上，每一个样本函数 xi (t ) 都是一个确定的数值 xi (t 1) ，但是每个 xi (t 1) 都是不可预知的，这正是随机过程随机性的体现。所以，在一个固定时刻 t 1 上，不同样本的取值 {xi (t 1),i =1,2,⋯,n } 是一个随机变量，记为 ξ (t 1) 。换句话说，随机过程在任意时刻的值是一个随机变量 (random variable) 。因此，又可以把随机过程看作是在时间进程中处于不同时刻的随机变量的集合。

1.随机过程的分布函数

设 ξ (t ) 表示一个随机过程，则它在任意时刻 t 1 的值 ξ (t 1) 是一个随机变量，其统计特性可以用分布函数 (distribution function) 或概率密度 (probability density) 函数来描述。把随机变量 ξ (t 1) 小于或等于某一数值 x 1 的概率 P [ξ (t 1)⩽x1] ，记作

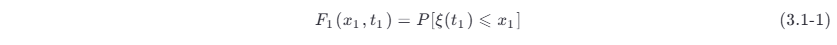
并称它为随机过程 ξ (t ) 的一维 (one dimensional) 分布函数。如果 F 1(x 1,t 1) 对 x1 的偏导 (partial derivative) 存在，有

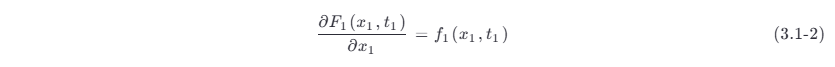
则称f 1( x 1, t 1) 为 ξ ( t ) 的一维概率密度函数 。显然，一维分布函数或一维概率密度函数仅仅描述了随机过程任一瞬间的统计特性，它对随机过程的描述很不充分。进而对于任意固定的 t 1 和 t 2 时刻，把 ξ (t 1)⩽x 1 和 ξ (t 2)⩽x2 同时成立的概率

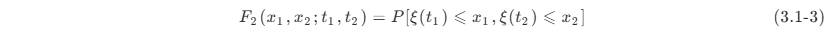
称为随机过程 ξ (t) 的二维分布函数。如果

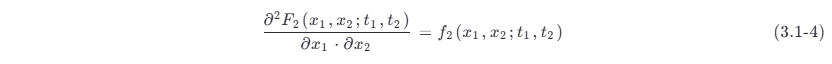
存在，则称 f 2(x 1,x 2;t 1,t 2) 为 ξ (t) 的二维概率密度函数。

同理，任意给定 t 1,t 2,⋯,tn ∈T ，则 ξ (t ) 的 n 维分布函数定义为

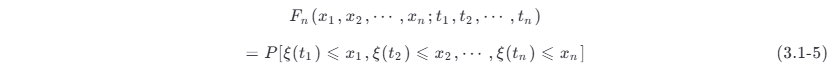
如果

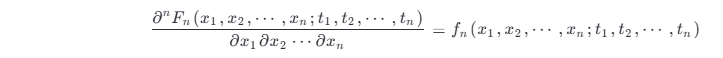
存在，则称其为 ξ (t ) 的 n 维概率密度函数。显然，n 越大，对随机过程统计特性的描述就越充分。

2.随机过程的数字特征

随机过程的数字特征是由随机变量的数字特征推广而得到的，其中最常用的是均值、方差和相关函数。

1. 均值（数学期望）

随机过程 ξ (t) 的均值 (average) 或称数学期望 (mathematical expectation)，定义为

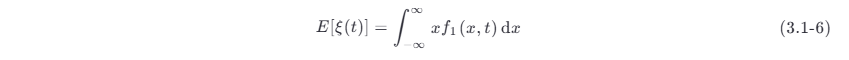
这是因为在任意给定时刻 t 1 的取值 ξ (t 1) 是一个随机变量，其概率密度函数为 f 1(x 1,t 1) ，则 ξ (t1) 的均值为

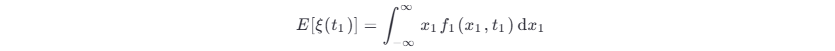
由于 t 1 是任取的，所以可以把 t 1 直接写为 t ，x 1 改为 x ，这时上式就变为随机过程在任意时刻 t 的均值，即式 (3.1-6)。

显然**，** ξ ( t ) 的均值 E [ ξ ( t )] 是时间的确定函数，常记为 a ( t ) ，它表示随机过程的 n 个样本函数曲线的摆动中心（如图中粗线所示）。

2.方差

随机过程的方差 (variance) 定义为

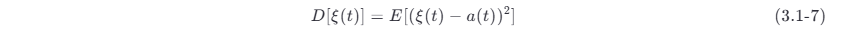
D [ξ (t )] 常记为 σ 2(t ) 。这里也把任意时刻 t 1 直接写成了 t 。因为

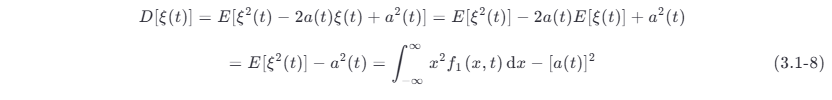
所以，方差等于均方值与均值平方之差 ，它表示随机过程在时刻 t 相对于均值 a ( t ) 的偏离程度。

3.相关函数

均值和方差都只与随机过程的一维概率密度函数有关，因而它们只是描述了随机过程在各个孤立时刻的特征，而不能反映随机过程内在的联系。为了衡量随机过程在任意两个时刻上获得的随机变量之间的关联程度，常采用相关函数 (correlation function) R ( t 1, t 2) 或协方差函数 (covariance function) B ( t 1, t 2) 。随机过程 ξ (t) 的协方差函数定义为

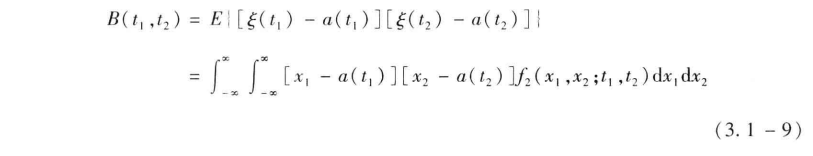
式中：a (t 1) 和 a (t 2) 分别是在 t 1 和 t 2 时刻得到的 ξ (t ) 的均值；f 2(x 1,x 2;t 1,t 2) 为 ξ (t) 的二维概率密度函数。

随机过程 ξ (t) 的相关函数定义为

式中：ξ (t 1) 和 ξ (t 2) 分别是在 t 1 和 t 2 时刻观测 ξ (t) 得到的随机变量。

可以看出，R (t 1,t 2) 是两个变量 t 1 与 t 2 的确定函数。R (t 1,t 2) 与 B (t 1,t2) 之间有着如下确定的关系：

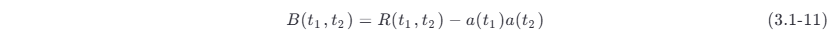
若随机过程的均值为 0，则 B (t 1,t 2) 与 R (t 1,t 2) 完全相同；即使均值不为 0，两者所描述的随机过程的特征也是一致的，今后将常用 R (t 1,t2) 。

如果把相关函数的概念引伸到两个或更多个随机过程，可以得到互相关函数。设 ξ (t ) 和 η (t) 分别表示两个随机过程，则互相关函数定义为

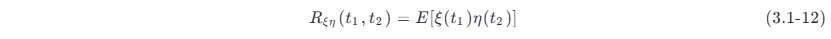
与此对比，由于R ( t 1, t 2) 是衡量同一过程的相关程度的，所以称它为自相关函数 。若 t 2>t 1 ，并令 τ =t 2−t 1 ，则相关函数 R (t 1,t 2) 可表示为 R (t 1,t 1+τ ) 。这说明，相关函数是 t 1 和 τ 的函数。

2.平稳随机过程

平稳随机过程 (stationary random process) 是一类应用非常广泛的随机过程，它在通信系统的研究中有着极其重要的意义。

1.定义

若一个随机过程 ξ ( t ) 的统计特性与时间起点无关，即时间平移不影响其任何统计特性，则称该随机过程是在严格意义下的平稳随机过程，简称严平稳随机过程。

因此，平稳随机过程 ξ ( t ) 的任意有限维概率密度函数与时间起点无关 ，也就是说，对于任意的正整数 n 和所有实数 Δ ，有

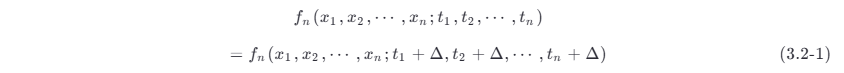
它的一维概率密度函数与时间 t 无关，即

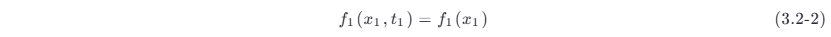
而二维分布函数只与时间间隔 τ =t 2−t1 有关，即

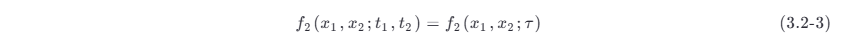
显然，随着概率密度函数的简化，平稳随机过程 ξ (t) 的一些数字特征也可以相应地简化，其均值和自相关函数分别为

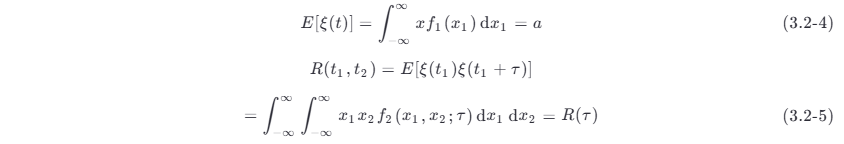
可见，平稳随机过程 ξ (t ) 具有简明的数字特征：① 均值与 t 无关，为常数 a ；② 自相关函数只与时间间隔 τ = t 2− t 1 有关，即 R ( t 1, t 1+ τ )= R ( τ )。实际上常用这两个条件来直接判断随机过程的平稳性，并把同时满足①和②的过程定义为广义平稳 (generalized stationary) 随机过程。显然，严平稳随机过程必定是广义平稳的，反之不一定成立。

2.各态历经性

随机过程的数字特征（均值、相关函数）是对随机过程的所有样本函数的统计平均，但在实际中常常很难测得大量的样本。因此，自然会提出这样一个问题：能否从一次试验而得到的一个样本函数 x (t ) 来决定平稳过程的数字特征呢？回答是肯定的。**平稳过程在满足一定的条件下具有一个有趣而又非常有用的特性，称为各态历经性 (ergodicity)（又称遍历性）。具有各态历经性的过程，其数字特征（均为统计平均）完全可由随机过程中的任一实现的时间平均值来代替。**下面，来讨论各态历经性的条件。

假设 x (t ) 是平稳过程 ξ (t) 的任意一次实现（样本），由于它是时间的确定函数，可以求得它的时间平均值。其时间均值和时间相关函数分别定义为

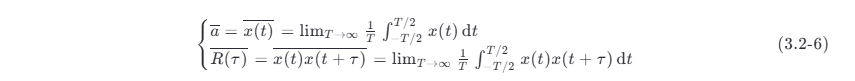
如果平稳过程使

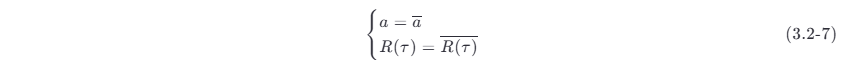
成立。也就是说，平稳过程的统计平均值等于它的任一次实现的时间平均值，则称该平稳过程具有各态历经性。

各态历经的含义：随机过程中的任一次实现都经历了随机过程的所有可能状态。 因此，关于各态历经性的一个直接结论是，**在求解各种统计平均（均值或自相关函数等）时，无需作无限多次的考察，只要获得一次实现的"时间平均"值代替过程的"统计平均"值即可，**从而使测量和计算的问题大为简化。

注意：具有各态历经性的随机过程一定是平稳过程，反之不一定成立。在通信系统中所遇到的随机信号和噪声，一般均能满足各态历经条件。

3.平稳过程的自相关函数

自相关函数是表述平稳过程特性的一个特别重要的函数。它不仅可以用来描述平稳过程的数字特征，它还与平稳过程的谱特性有着内在的联系。可以通过它的性质来说明这一点。

设 ξ (t) 为实平稳随机过程，则它的自相关函数

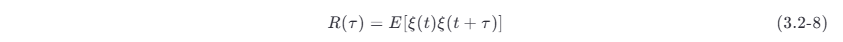
具有如下主要性质：

R (0)=E [ξ^ 2(t )] ，表示 ξ (t) 的平均功率。

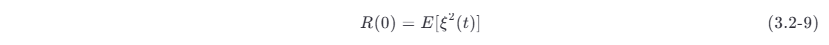
R (τ )=R (−τ ) ，表示 τ 的偶函数

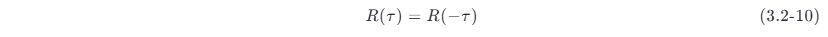
上述性质可直接由定义式 (3.2-8) 得证

∣R (τ )∣⩽R (0) ，表示 R (τ ) 在 τ =0 有最大值。考虑一个非负式 E [ξ (t )±ξ (t +τ)]^2⩾0 可以证明此关系。
R (∞)=E^ 2[ξ (t )]=a^ 2 ，表示 ξ (t) 的直流功率

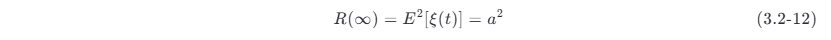
这是因为

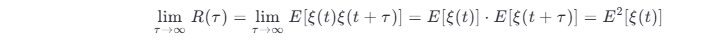
上式利用了当 τ →∞ 时，ξ (t ) 与 ξ (t +τ) 没有任何依赖关系，即统计独立。

R (0)−R (∞)=*σ^*2

4.平稳过程的功率谱密度

随机过程的频谱特性可以用它的功率谱密度来表述。随机过程中的任一样本是一个确定的功率型信号 。对于任意的确定功率信号 f (t) ，它的功率谱密度定义为

不妨把 f (t ) 看成是平稳过程 ξ (t ) 的任一样本，因而每个样本的功率谱密度也可用式 (3.2-14) 来表示。一般而言，不同样本函数具有不同的谱密度 Pf ( f ) ，因此，某一样本的功率谱密度不能作为过程的功率谱密度。过程的功率谱密度应看作是对所有样本的功率谱的统计平均，即

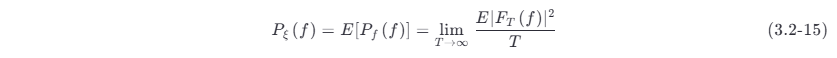
式 (3.2-15) 给出了平稳过程 ξ (t ) 的功率谱密度 Pξ (f ) 定义，尽管该定义相当直观，但直接用它来计算功率谱密度却并不简单。那么，如何方便地求功率谱 Pξ (f) 呢？

非周期的功率型确知信号的自相关函数与其功率谱密度是一对傅里叶变换 。这种关系对平稳随机过程同样成立，也就是说，平稳过程的功率谱密度 Pξ ( f ) 与其自相关函数 R ( τ ) 也是一对傅里叶变换关系，即

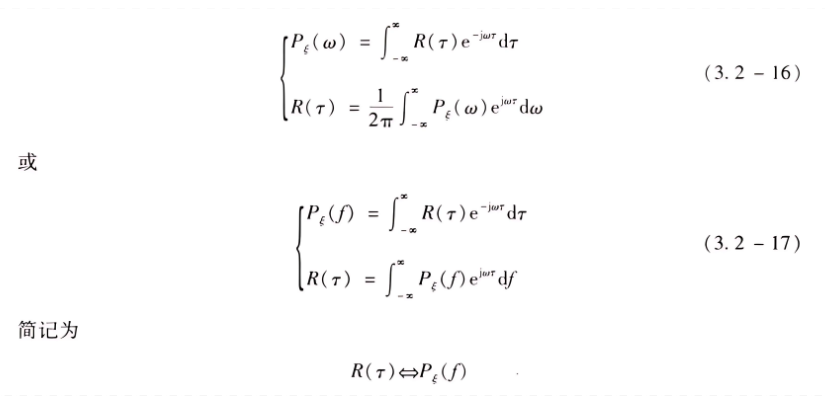
以上关系称为维纳---辛钦 (Wiener-Khinchine) 定理 。它在平稳随机过程的理论和应用中是一个非常重要的工具，它是联系频域和时域两种分析方法的基本关系式。

在维纳---辛钦关系的基础上，可以得到以下结论：

对功率谱密度进行积分，可以得到平稳过程的平均功率：

这正是维纳---辛钦关系的意义所在，它不仅指出了用自相关函数来表示功率谱密度的方法，同时还从频域的角度给出了过程 ξ (t ) 平均功率的计算法，而式 R (0)=E [ξ^ 2(t )] 是时域计算法。这一点进一步验证了 R (τ ) 与功率谱 Pξ (f) 的关系

各态历经过程的任一样本函数的功率谱密度等于过程的功率谱密度。也就是说，每一样本函数的谱特性都能很好地表现整个过程的谱特性。
功率谱密度 Pξ (f) 具有非负性和实偶性，即有

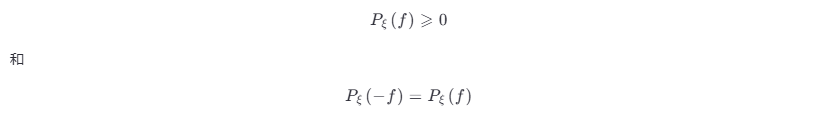
这与 R (τ) 的实偶性相对应。

3.高斯随机过程

高斯过程 (Gaussian process)，也称正态随机过程 (normal random process)，是通信领域中最重要也是最常见的过程。

1. 定义

如果随机过程 ξ ( t ) 的任意 n 维 ( n =1,2,⋯ ) 分布均服从正态分布，则称它为正态过程或高斯过程 。其 n 维正态概率密度函数表示如下：

2.重要性质

由式 (3.3-1) 可以看出，高斯过程的 n -维分布只依赖各个随机变量的均值、方差和归一化协方差。因此，对于高斯过程，只需要研究它的数字特征就可以了。
广义平稳的高斯过程也是严平稳的。因为，若高斯过程是广义平稳的，即其均值与时间无关，协方差函数只与时间间隔有关，而与时间起点无关，则它的 n -维分布也与时间起点无关，故它也是严平稳的。所以，高斯过程若是广义平稳的，则也严平稳。
如果高斯过程在不同时刻的取值是不相关的，即对所有 j≠k 有 bjk=0 ，这时式 (3.3-1) 简化为

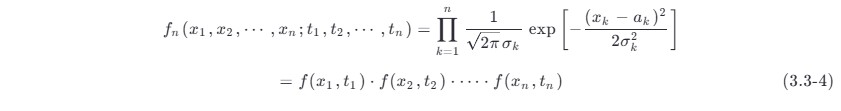
这表明，如果高斯过程在不同时刻的取值是不相关的，那么它们也是统计独立的。

高斯过程经过线性变换后生成的过程仍是高斯过程。也可以说，若线性系统的输入为高斯过程，则系统输出也是高斯过程。

3. 高斯随机变量

高斯过程在任一时刻上的取值是一个正态分布的随机变量，也称高斯随机变量，其一维概率密度函数为

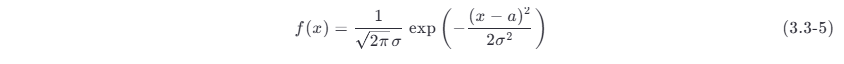
式中：a 和 σ 2 分别为高斯随机变量的均值和方差；f (x) 曲线如图所示。

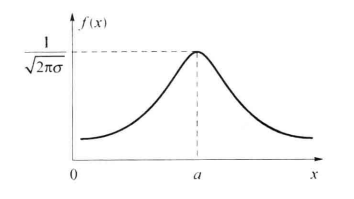
由式 (3.3-5) 及图 3-3 可以看出正态分布的概率密度 f (x) 有以下特性：

f (x ) 对称于 x =a 这条直线，即

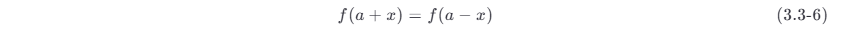
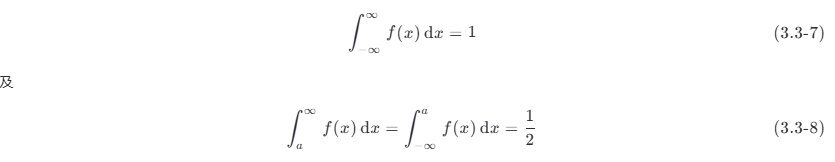
a 表示分布中心，σ 称为标准偏差，表示集中程度。f (x ) 图形将随着 σ 的减小而变高和变窄。当 a =0 ，σ=1 时，称为标准化的正态分布，即

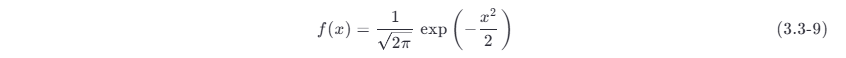
在通信系统的性能分析中，常需要计算高斯随机变量 ξ 小于或等于某一取值 x 的概率 P (ξ ⩽x ) ，它等于概率密度 f (x ) 的积分。把正态分布的概率密度 f (x) 积分定义为正态分布函数，它可表示为

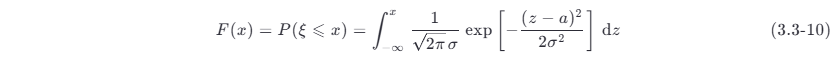
这个积分的值无法用闭合形式计算，一般把这个积分式与可以在数学手册上查出函数值的一些特殊函数联系起来计算其值。

另一种经常用于表示高斯曲线尾部下的面积的函数记为 Q ( x ) ，其定义为

4.平稳随机过程通过线性系统

随机过程通过线性系统的分析，完全是建立在确知信号通过线性系统的分析基础之上的。线性时不变 (time-invariant) 系统可由其单位冲激响应 h ( t ) 或其频率响应 H ( f ) 表征 。若令 vi (t ) 为输入信号，vo (t) 为输出信号，则输入与输出关系可以表示成卷积 (convolution)，即

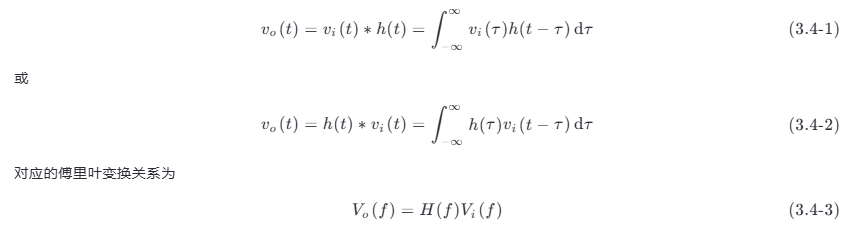
如果把 vi (t ) 看作是输入随机过程的一个样本，则 vo (t ) 是输出随机过程的一个样本。那么，当该线性系统的输入端加入一个随机过程 ξi (t ) 时，对于 ξi (t ) 的每个样本 [vi ,n (t ),n =1,2,⋯] ，系统的输出都有一个 [vo ,n (t ),n=1,2,⋯] 与其相对应，它们之间满足式 (3.4-2)，即

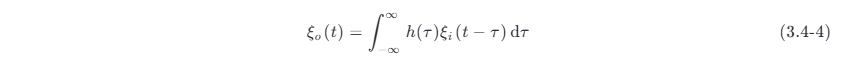
利用这个关系式，在假设输入过程 ξi (t ) 是平稳的，其均值为 a ，自相关函数为 Ri (τ ) ，功率谱密度为 Pi (ω ) 的基础上，求输出过程 ξo (t) 的统计特性，即它的均值、自相关函数、功率谱以及概率分布

输出过程 ξo (t) 的均值

对式 (3.4-4) 两边取统计平均，有

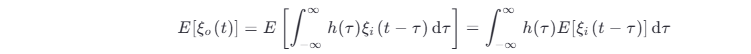
设输入过程是平稳的，则有 E [ξi (t −τ )]=E [ξi (t )]=a （常数），所以

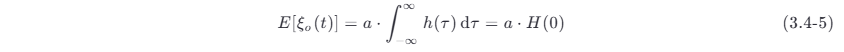
式中：H (0) 为线性系统在 f =0 处的频率响应，即直流增益 。因此输出过程的均值 E [ξo (t)] 是一个常数。

输出过程 ξo (t) 的自相关函数

根据自相关函数的定义，输出过程的自相关函数为

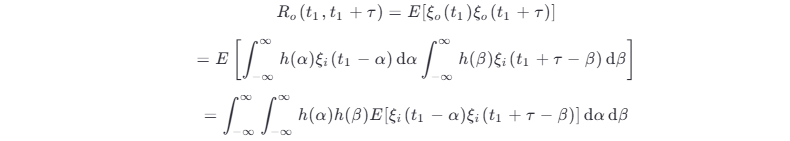
根据输入过程的平稳性，有

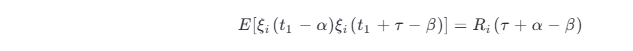
于是

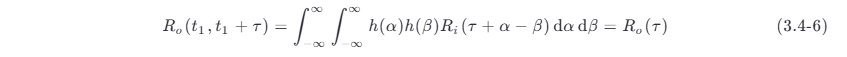
式 (3.4-6) 表明，输出过程的自相关函数仅仅是时间间隔 τ 的函数 。由式 (3.4-5) 和式 (3.4-6) 可知，若线性系统的输入过程是平稳的，那么输出过程也是平稳的。

输出过程 ξo (t) 的功率谱密度

对式 (3.4-6) 进行傅里叶变换，有

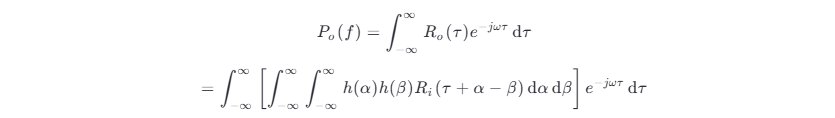
对上式进行变量代换，令 τ ′=τ +α −β ，则

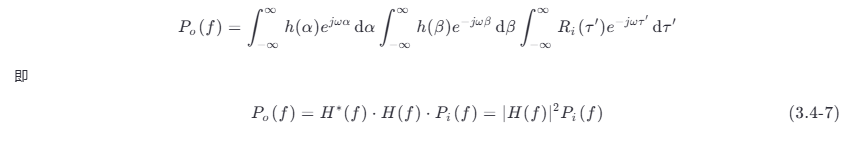
得到一个重要结论：输出过程的功率谱密度是输入过程的功率谱密度乘以系统频率响应模值的平方 。当要求的是输出过程的自相关函数 Ro (τ ) 时，较容易的方法是先求功率谱密度 Po (f ) ，然后计算其傅里叶反变换，这常常比直接计算 Ro (τ) 要简便得多。

输出过程 ξo (t) 的概率分布

一般来说，在已知输入过程概率分布的情况下，总可以通过式 (3.4-4) 来确定输出过程的概率分布。一种经常能够遇到的实际情况是：如果线性系统的输入过程是高斯型的，则系统的输出过程也是高斯型的。这是因为从积分原理来看，式 (3.4-4) 可表示为一个和式的极限，即

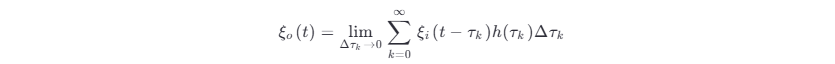
由于 ξi (t ) 已假设是高斯型的，所以上式右端的每一项 ξi (t −τk )h (τk )Δτk 在任一时刻上都是一个高斯随机变量。因此，输出过程在任一时刻上得到的随机变量就是这无限多个高斯随机变量之和。由概率论理论得知，这个"和"随机变量也是高斯随机变量，因而输出过程也为高斯过程。但要注意，由于线性系统的介入，与输入高斯过程相比，输出过程的数字特征已经改变了。

更一般地说，高斯过程经线性变换后的过程仍为高斯过程。

5.窄带随机过程

若随机过程 ξ ( t ) 的谱密度集中在中心频率 fc 附近相对窄的频带范围 Δ f 内，即满足 Δ f ≪ fc 条件，且 fc 远离零频率，则称该 ξ ( t ) 为窄带随机过程。实际中，大多数通信系统都是窄带带通型的，通过窄带系统的信号或噪声必然是窄带随机过程。

一个典型的窄带随机过程的频谱密度和波形如图所示

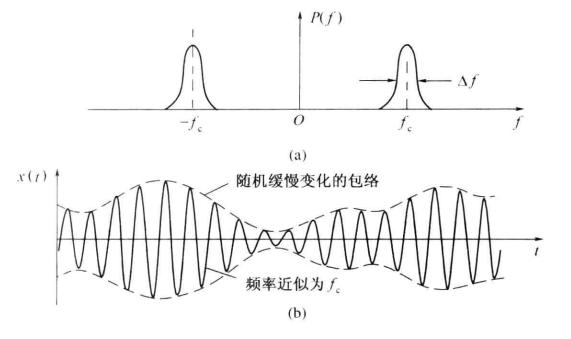
可见，窄带随机过程的一个样本的波形如同一个包络和相位随机缓变的正弦波。因此，窄带随机过程 ξ (t) 可表示为

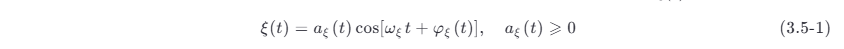
式中：aξ (t ) 及 φξ (t ) 分别为窄带随机过程 ξ (t ) 的随机包络和随机相位；ωc为正弦波的中心角频率。

将式 (3.5-1) 进行三角函数展开，可以改写为

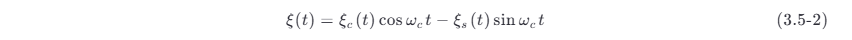
其中

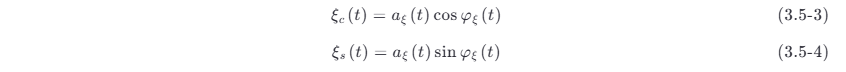
这里的ξc ( t ) 及 ξs ( t ) 分别称为 ξ ( t ) 的同相分量和正交分量 。由式 (3.5-1) 和式 (3.5-2) 看出，ξ (t ) 的统计特性可以由 aξ (t ),φξ (t ) 或 ξc (t ),ξs (t ) 的统计特性确定。反之，若窄带过程 ξ (t ) 的统计特性已知，则 aξ (t ),φξ (t ) 或 ξc (t ),ξs (t ) 的统计特性也随之可以确定。作为一个今后特别有用的例子，假设 ξ (t ) 是一个均值为 0，方差为 σξ 2 的平稳高斯窄带过程，来分析 aξ (t ),φξ (t ) 及 ξc (t ),ξs (t) 的统计特性。

1. ξc (t ) 和 ξs (t) 的统计特性

对式 (3.5-2) 求数学期望：

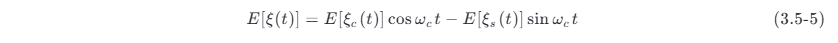
因为 ξ (t ) 平稳且均值为零，那么对于任意的时间 t ，都有 E [ξ (t)]=0 ，所以由式 (3.5-5)，得

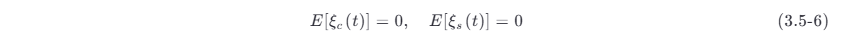
由自相关函数的定义式 (3.2-8) 和式 (3.5-2)，可得 ξ (t) 的自相关函数为

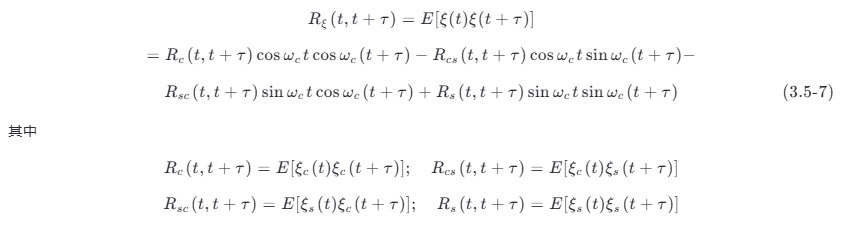
因为 ξ (t) 是平稳的，故有

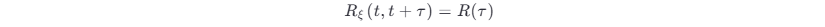
这就要求式 (3.5-7) 的右端与时间 t 无关，而仅与 τ 有关。因此，若令 t=0 ，式 (3.5-7) 仍应成立，它变为

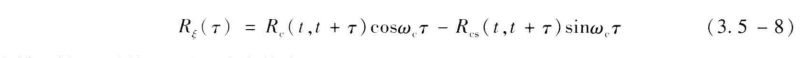
因与时间 t 无关，以下两式自然成立：

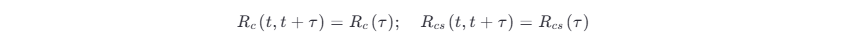
所以，式 (3.5-8) 变为

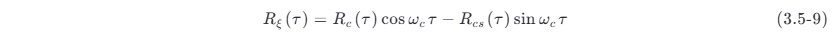
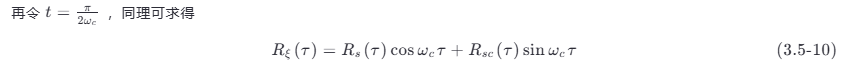
其中 Rs (t ,t +τ )=Rs (τ );Rsc (t ,t +τ )=Rsc (τ)

由以上分析可知，若窄带过程 ξ (t ) 是平稳的，则 ξc (t ) 与 ξs (t) 也必然是平稳的。

进一步分析，式 (3.5-9) 和式 (3.5-10) 应同时成立，故有

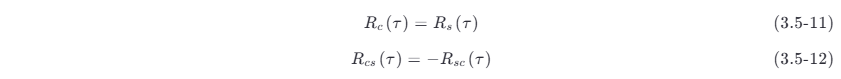
式 (3.5-11) 表明，同相分量 ξc (t ) 和正交分量 ξs (t) 具有相同的自相关函数。根据互相关函数的性质，应有

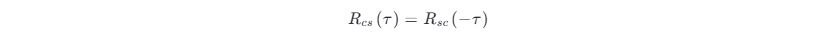
将上式代入式 (3.5-12)，可得

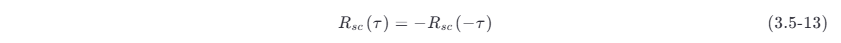
式 (3.5-13) 表明 Rsc (τ ) 是 τ 的奇函数，所以

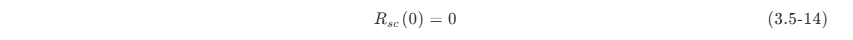
同理可证

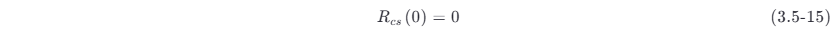
于是，由式 (3.5-9) 及式 (3.5-10)，得

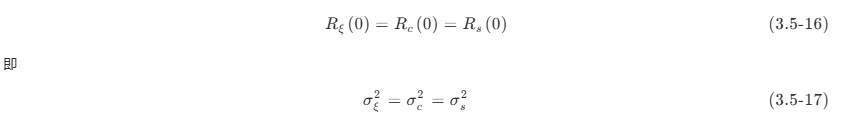
这表明 ξ (t ),ξc (t ) 和 ξs (t) 具有相同的平均功率或方差（因为均值为 0）。

另外，根据平稳性，过程的特性与 t 变量无关，故由式 (3.5-2) 可得：

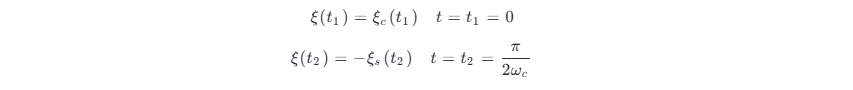
因为 ξ (t ) 是高斯过程，所以 ξc (t 1),ξs (t 2) 一定是高斯随机变量，从而 ξc (t ),ξs (t ) 也是高斯过程。根据式 (3.5-15) 可知，ξc (t ) 与 ξs (t ) 在 τ =0 处互不相关，又由于它们是高斯型的，因此 ξc (t ) 与 ξs (t) 也统计独立。

综上所述，得到一个重要结论：一个均值为零的窄带平稳高斯过程 ξ ( t ) ，它的同相分量 ξc ( t ) 和正交分量 ξs ( t ) 同样是平稳高斯过程，而且均值为零，方差也相同 。此外，在同一时刻上得到的 ξc 和 ξs 是互不相关的或统计独立的。

2. aξ (t ) 和 φξ (t) 的统计特性

由上面的分析可知，ξc 和 ξs 的联合概率密度函数为

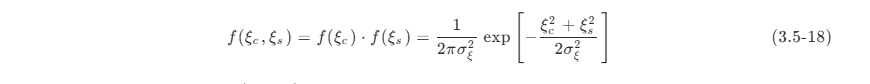
设 aξ ,φξ 的联合概率密度函数为 f (aξ ,φξ) ，则根据概率论知识有

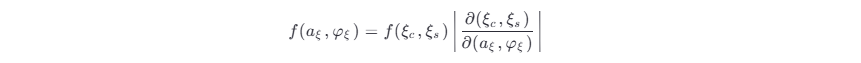
根据式 (3.5-3) 和式 (3.5-4) 在 t 时刻随机变量之间的关系

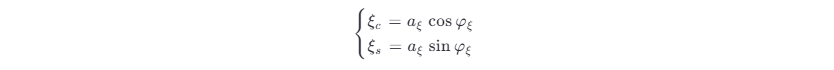
可以求得

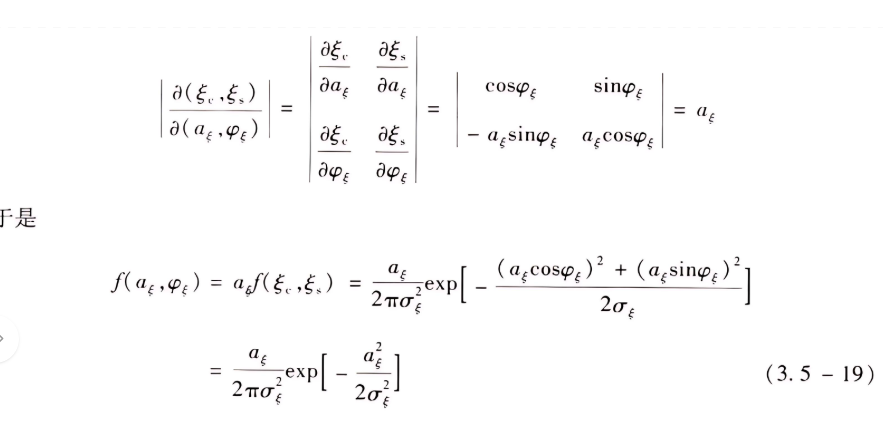
注意：这里 aξ ⩾0 ，而 φξ 在 (0,2π) 内取值。

再利用概率论中的边际分布关系，将 f (aξ ,φξ ) 对 φξ 积分求得包络 aξ 的一维概率密度函数为

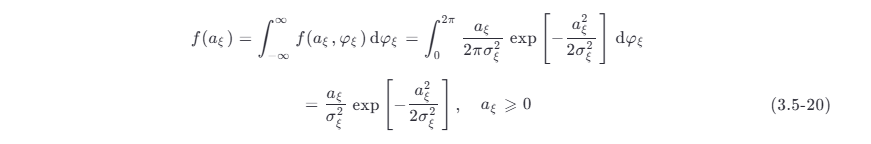
可见，aξ 服从瑞利 (Rayleigh) 分布。

由 f (aξ ,φξ ) 对 aξ 积分求得相位 φξ 的一维概率密度函数

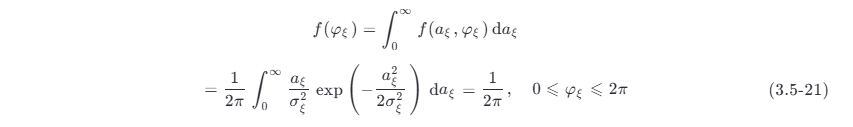
可见，φξ 服从均匀分布。

综上所述，又得到一个重要结论：一个均值为零、方差为 σξ^ 2 的窄带平稳高斯过程 ξ ( t ) ，其包络 aξ ( t ) 的一维分布是瑞利分布，相位 φξ ( t ) 的一维分布是均匀分布，并且就一维分布而言， aξ ( t ) 与 φξ ( t ) 是统计独立的，即

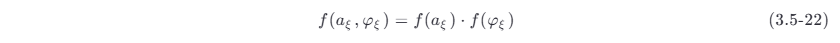
6.正弦波加窄带高斯噪声

传输的信号是用正弦波作为载波的已调信号。当信号经过信道传输时总会受到噪声的影响，通常在解调器前端设置一个带通滤波器，以滤除信号频带以外的噪声。

设正弦波加窄带高斯噪声的混合信号为

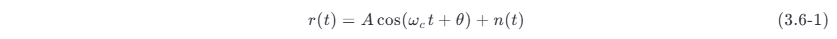
式中：n (t )=nc (t )cosωct −ns (t )sinωct （式 (3.5-2)），为窄带高斯噪声，其均值为零，方差为 σn^ 2 ；θ 为正弦波的随机相位，在 (0,2π ) 上均匀分布；振幅 A 和角频率 ωc 均假定为确知量

于是

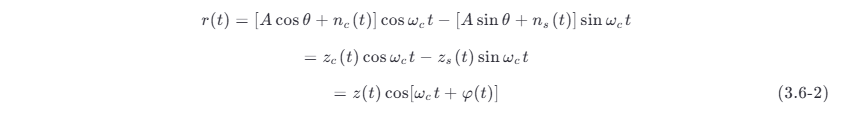
其中

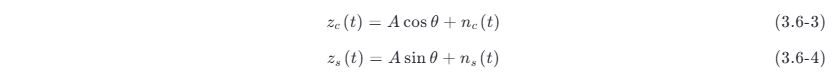
r (t) 的包络和相位分别为

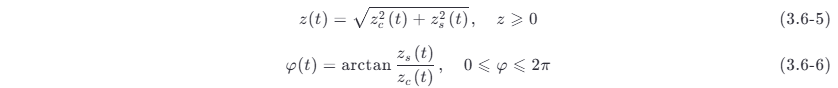
最为关心的是 r (t ) 的包络和相位的统计特性。利用 3.5 节的结果，如果 θ 值已给定，则 zc ,zs 是相互独立的高斯随机变量，且有

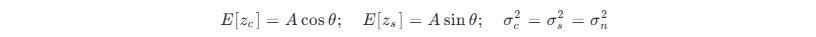
所以，在给定相位 θ 的条件下的 zc 和 zs 的联合概率密度函数为

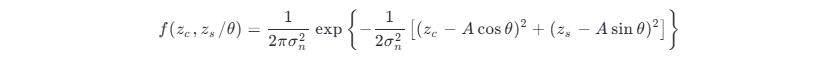
利用与 3.5 节分析 aξ ,φξ 相似的方法，根据 zc ,zs 与 z ,φ 之间的随机变量关系

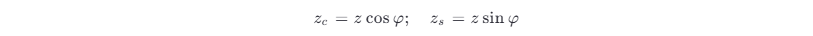
可以求得在给定相位 θ 的条件下的 z 与 φ 的联合概率密度函数为

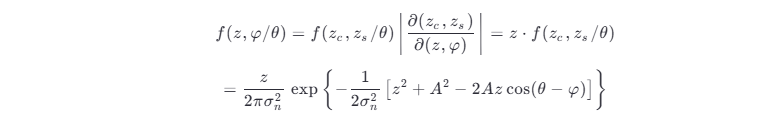
然后求给定 θ 条件下的边际分布，即

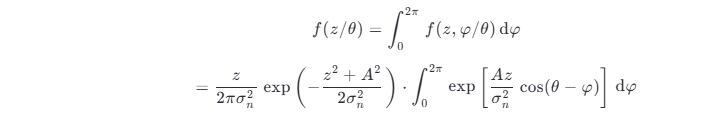
由于

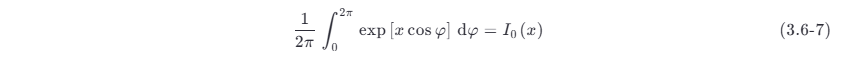
故有

当 x ⩾0 时，I 0(x ) 是单调上升函数，且有 I0(0)=1 ，因此

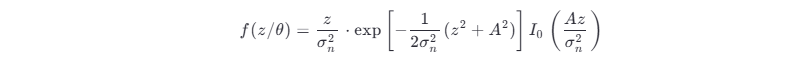
由上式可见，f (z /θ ) 与 θ 无关，故 r (t ) 的包络 z 的概率密度函数为

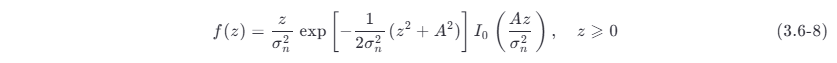
这个概率密度函数称为广义瑞利分布，又称莱斯 (Rice) 分布。

式 (3.6-8) 存在两种极限情况：

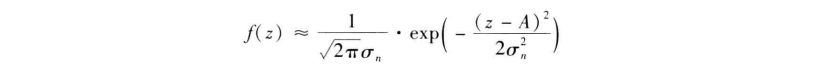
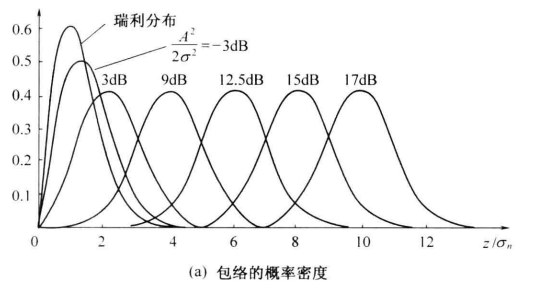
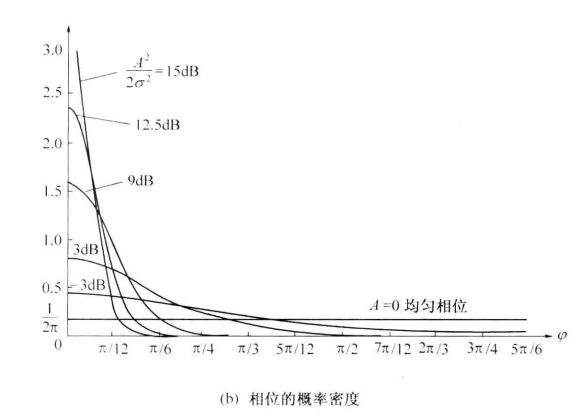
由此可见，正弦波加窄带高斯噪声的包络分布 f (z ) 与信噪比有关。小信噪比时， f ( z ) 接近于瑞利分布；大信噪比时， f ( z ) 接近于高斯分布；在一般情况下， f ( z ) 才是莱斯分布 。图给出了不同的 γ 值时 f (z) 的曲线。

7.高斯白噪声和带限白噪声

常用高斯白噪声作为通信信道中的噪声模型。

因为通信系统中常见的热噪声近似为白噪声，且热噪声的取值恰好服从高斯分布 。另外，实际信道或滤波器的带宽存在一定限制，白噪声通过后，其结果是带限噪声 ，若其谱密度在通带范围内仍具有白色特性，则称其为带限白噪声 (band-limited white noise) ，它又可以分为低通白噪声和带通白噪声。

1.白噪声

如果噪声的功率谱密度在所有频率上均为一常数，即

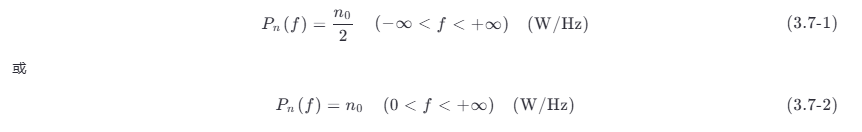
式中：n 0 为正常数，则称该噪声为白噪声，用 n ( t ) 表示。

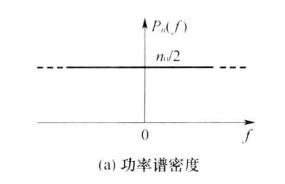
式 (3.7-1) 为双边功率谱密度，如图(a) 所示，而式 (3.7-2) 表示单边功率谱密度。

对式 (3.7-1) 取傅里叶反变换，可得到白噪声的自相关函数为

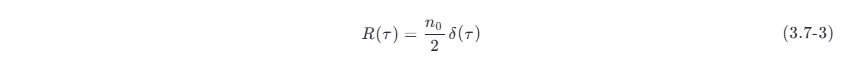
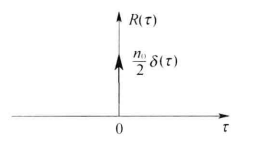
如图 (b) 所示，对于所有的 τ≠ 0 都有 R (τ )=0 ，这表明白噪声仅在 τ =0 时才相关，而在任意两个时刻（即 *τ≠*0 ）的随机变量都是不相关的。

由于白噪声的带宽无限，其平均功率为无穷大，即

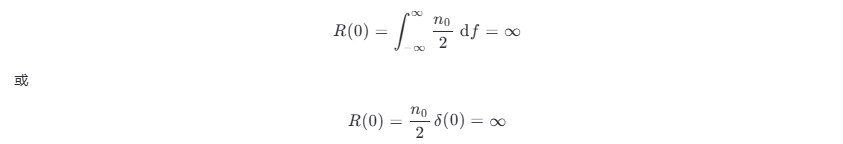
因此，真正"白"的噪声是不存在的，它只是构造的一种理想化的噪声形式，其中"白"和白光中的"白"有相同的意思；白光指在电磁辐射可见范围内所有频率分量的数值都相等

白噪声作为一个很有用的数学抽象，可以使问题的分析大大简化。在实际中，只要噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频段，就可以把它视为白噪声

如果白噪声取值的概率分布服从高斯分布，则称为高斯白噪声 ，常用它作为通信信道中的噪声模型。高斯白噪声在任意两个不同时刻上的随机变量之间，不仅是互不相关的，而且还是统计独立的。

2.低通白噪声

如果白噪声通过理想矩形的低通滤波器或理想低通信道，则输出的噪声称为低通 (lowpass) 白噪声 ，也用 n (t ) 表示。假设理想低通滤波器具有模为 1、截止频率为 ∣f ∣⩽fH 的传输特性，则低通白噪声对应的功率谱密度为

自相关函数为

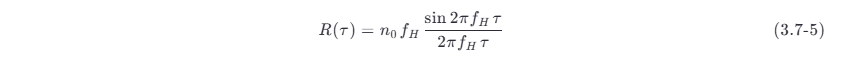
对应的曲线如图所示。

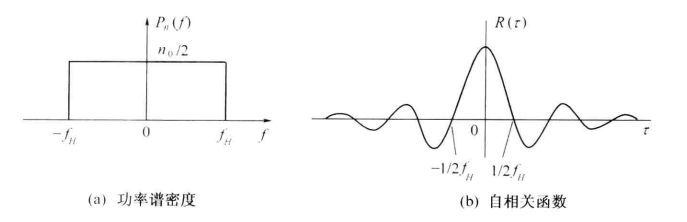
由图 (a) 可见，白噪声的功率谱密度被限制在 ∣ f ∣⩽ fH 内，在此范围外则为零，通常把这样的噪声也称为带限白噪声。

由图(b) 可以看出，这种带限白噪声只有在 τ =k /2fH （k=1,2,3,⋯ ）上得到的随机变量才不相关。也就是说，如果按抽样定理（见第 10 章）对带限白噪声进行抽样的话，各抽样值是互不相关的随机变量。这是一个很重要的概念。

3.带通白噪声

如果白噪声通过理想矩形的带通 (bandpass) 滤波器或理想带通信道，则其输出的噪声称为带通白噪声 ，仍用 n (t) 表示。

设理想带通滤波器的传输特性为

式中：fc 为中心频率；B 为通带宽度。

则其输出噪声的功率谱密度为

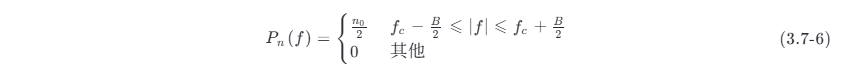
自相关函数为

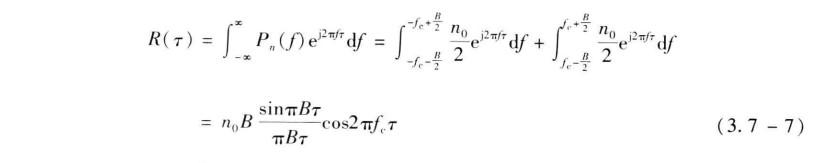
对应的曲线如图所示。

通常，带通滤波器的 B ≪ fc **，因此也称窄带 (narrowband) 滤波器，相应地把带通白噪声称为窄带高斯白噪声，**因此它的表达式和统计特性与 3.5 节所描述的一般窄带随机过程相同，即

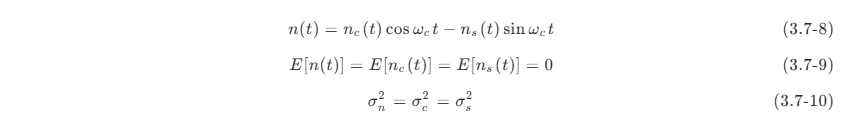
式 (3.7-10) 表明 n (t ),nc (t ) 和 n (t ) 具有相同的平均功率（因为均值为 0）。根据图所示的功率谱密度曲线，很容易求出 n (t) 的平均功率为

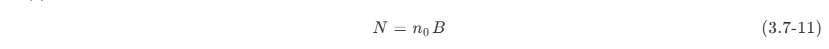
这里 B 是指理想矩形的带通滤波器的带宽，而对于实际的带通滤波器， B 应是噪声等效 (equivalent) 带宽（见 4.5 节）