用深度强化学习玩Atari游戏

温馨提示：

摘要

我们提出了第一个能够使用强化学习，直接从高维感知输入中成功学习控制策略的深度学习模型。该模型是一个卷积神经网络，使用Q-learning的一种变体进行训练，其输入为原始像素，输出为一个值函数，用于估计未来的奖励。我们将该方法应用于Arcade Learning Environment中的七款Atari 2600游戏，且无需对网络结构或学习算法进行调整。结果显示，在六款游戏中，该方法的表现优于所有以往的方法，并在其中三款游戏中超过了人类专家的水平。

1 引言

从高维感知输入（如视觉和语音）中直接学习控制智能体的策略，是强化学习（RL）长期以来面临的一个挑战。在这类任务中，大多数成功的RL应用依赖于人工设计的特征，再结合线性值函数或策略表示。显然，这类系统的性能在很大程度上依赖于特征表示的质量。

近年来，深度学习的进展使得从原始感知数据中提取高层特征成为可能，进而推动了计算机视觉 [11, 22, 16] 和语音识别 [6, 7] 等领域的突破。这些方法利用了各种神经网络结构，包括卷积网络、多层感知机、受限玻尔兹曼机和循环神经网络，并结合了监督学习和无监督学习技术。因此，一个自然而然的问题是，类似的技术是否也能为感知数据上的强化学习带来收益。

然而，从深度学习的角度来看，强化学习带来了若干挑战。首先，迄今为止多数成功的深度学习应用都依赖大量人工标注的训练数据；而强化学习算法则必须从一个标量的奖励信号中进行学习，这种奖励信号通常是稀疏的、有噪声的、且存在延迟。这种从动作到奖励可能跨越数千步的延迟，相较于监督学习中输入与目标之间的直接关联，显得尤为棘手。另一个问题是，大多数深度学习算法都假设数据样本是独立同分布的，而在强化学习中，状态序列通常具有高度相关性。此外，在RL中，随着算法学习出新的行为，数据分布也会发生变化，这对依赖固定分布的深度学习方法来说可能构成难题。

本文展示了一个卷积神经网络如何克服上述难题，在复杂的强化学习环境中，从原始视频数据中学习出成功的控制策略。该网络使用Q-learning [26] 的一种变体进行训练，通过随机梯度下降来更新权重。为缓解数据相关性和非平稳分布的问题，我们引入了"经验回放"机制 [13]，从过去的转移中随机采样，以此平滑训练过程中的数据分布。

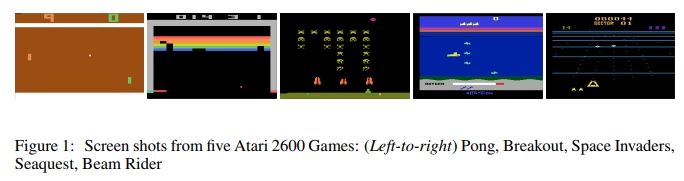
我们将所提出的方法应用于一系列由 Arcade Learning Environment（ALE）[3] 实现的 Atari 2600 游戏。Atari 2600 是一个具有挑战性的强化学习测试平台，它为智能体提供高维度的视觉输入（210×160 的 RGB 视频，每秒60帧），并包含一组多样且颇具趣味性的任务，这些任务本身就是为难倒人类玩家而设计的。我们的目标是构建一个单一的神经网络智能体，能够尽可能多地成功学习玩这些游戏。该网络没有接收到任何关于具体游戏的信息或人工设计的视觉特征，也无法访问模拟器的内部状态；它仅仅依赖视频输入、奖励与终止信号以及一组可执行动作进行学习------与人类玩家的情况完全一致。此外，网络结构及其训练所用的所有超参数在所有游戏中都保持不变。截至目前，在我们尝试的七款游戏中，该网络在六款游戏上的表现超越了所有以往的强化学习算法，并在其中三款游戏中超过了人类专家玩家的水平。图1展示了用于训练的五款游戏的截图样例。

2 背景

我们研究的是这样一类任务：智能体与环境 ε \varepsilon ε（在本研究中为 Atari 模拟器）通过一系列动作、观测和奖励进行交互。在每个时间步，智能体从合法动作集合 A = { 1 , ... , K } \mathcal { A } = \{ 1 , \ldots , K \} A={1,...,K} 中选择一个动作 a t a_t at。该动作会被传递给模拟器，从而改变其内部状态和游戏得分。一般情况下，环境 ε \varepsilon ε 可能是随机的。智能体无法观测 模拟器的内部状态；相反，它观测到的是来自模拟器的一张图像 x t ∈ R d x_t \in \mathbb{R}^d xt∈Rd，该图像是表示当前屏幕的原始像素值向量。此外，智能体还接收到一个奖励 r t r_t rt，表示游戏得分的变化。注意，游戏得分通常依赖于此前整段动作和观测序列；对于某个动作的反馈，可能需要经过成千上万个时间步才能收到。

由于智能体只能观测当前屏幕的图像，因此任务是部分可观测 的，许多模拟器状态在视觉上是不可区分的（即存在感知混淆 ）：仅凭当前屏幕 x t x_t xt 无法完全理解当前的情境。因此，我们考虑动作与观测的序列 s t = x 1 , a 1 , x 2 , ... , a t − 1 , x t s_t = x_1, a_1, x_2, \dots, a_{t-1}, x_t st=x1,a1,x2,...,at−1,xt，并学习依赖这些序列的游戏策略。我们假设模拟器中的所有序列在有限步内终止。该形式化方式构成了一个大但有限的马尔可夫决策过程（MDP），其中每个序列对应一个唯一的状态。因此，我们可以直接将标准的强化学习方法应用于该MDP，只需将完整的序列 s t s_t st 作为时间 t t t 时的状态表示即可。

智能体的目标是在与模拟器的交互中选择动作，以最大化未来的奖励。我们采用标准假设：未来奖励以折扣因子 γ \gamma γ 按时间步进行衰减，并定义时间 t t t 时的未来折扣回报为：

R t = ∑ t ′ = t T γ t ′ − t r t ′ R_t = \sum_{t'=t}^{T} \gamma^{t' - t} r_{t'} Rt=t′=t∑Tγt′−trt′

其中 T T T 是游戏终止时的时间步。

我们定义最优动作-价值函数 Q ∗ ( s , a ) Q^*(s, a) Q∗(s,a) 为：在观察到某个序列 s s s 并采取某个动作 a a a 后，按某种策略 π \pi π 行动所能获得的最大期望回报：

Q ∗ ( s , a ) = max ⁡ π E [ R t ∣ s t = s , a t = a , π ] Q^*(s, a) = \max_{\pi} \mathbb{E}[R_t \mid s_t = s, a_t = a, \pi] Q∗(s,a)=πmaxE[Rt∣st=s,at=a,π]

其中 π \pi π 是将序列映射为动作（或动作分布）的一种策略。

最优动作-价值函数满足一个重要的恒等式，称为Bellman方程 。其核心直觉如下：如果下一时间步序列 s ′ s' s′ 对于所有可能的动作 a ′ a' a′ 的最优值 Q ∗ ( s ′ , a ′ ) Q^*(s', a') Q∗(s′,a′) 都已知，那么最优策略就是选择能最大化预期值 r + γ Q ∗ ( s ′ , a ′ ) r + \gamma Q^*(s', a') r+γQ∗(s′,a′) 的动作 a ′ a' a′。
Q ∗ ( s , a ) = E s ′ ∼ E [ r + γ max ⁡ a ′ Q ∗ ( s ′ , a ′ ) ∣ s , a ] ( 1 ) Q ^ { * } ( s , a ) = \mathbb { E } _ { s ^ { \prime } \sim \mathcal { E } } \left[ r + \gamma \operatorname* { m a x } _ { a ^ { \prime } } Q ^ { * } ( s ^ { \prime } , a ^ { \prime } ) \Big | s , a \right]\quad(1) Q∗(s,a)=Es′∼E[r+γa′maxQ∗(s′,a′) s,a](1)

许多强化学习算法背后的基本思想是，通过使用 Bellman 方程作为迭代更新规则来估计动作-价值函数，其形式如下：

Q i + 1 ( s , a ) = E [ r + γ max ⁡ a ′ Q i ( s ′ , a ′ ) ∣ s , a ] Q_{i+1}(s, a) = \mathbb{E} \left[ r + \gamma \max_{a'} Q_i(s', a') \mid s, a \right] Qi+1(s,a)=E[r+γa′maxQi(s′,a′)∣s,a]

这样的值迭代算法会逐步收敛到最优动作-价值函数，即 Q i → Q ∗ Q_i \to Q^* Qi→Q∗ 当 i → ∞ i \to \infty i→∞ [23]。

然而，在实际中，这种基本方法是完全不可行的，因为动作-价值函数是针对每个状态序列分别估计的 ，没有任何泛化能力。因此，更常见的做法是使用一个函数逼近器来估计动作-价值函数：

Q ( s , a ; θ ) ≈ Q ∗ ( s , a ) Q(s, a; \theta) \approx Q^*(s, a) Q(s,a;θ)≈Q∗(s,a)

在强化学习领域中，这类函数逼近器通常是线性的，但有时也会使用非线性函数逼近器，例如神经网络。我们将带有权重参数 θ \theta θ 的神经网络函数逼近器称为 Q网络（Q-network） 。Q 网络可以通过最小化一系列随迭代 i i i 而变化的损失函数 L i ( θ i ) L_i(\theta_i) Li(θi) 来进行训练。

L i ( θ i ) = E s , a ∼ ρ ( ⋅ ) [ ( y i − Q ( s , a ; θ i ) ) 2 ] ( 2 ) L _ { i } \left( \theta _ { i } \right) = \mathbb { E } _ { s , a \sim \rho ( \cdot ) } \left[ \left( y _ { i } - Q \left( s , a ; \theta _ { i } \right) \right) ^ { 2 } \right]\quad(2) Li(θi)=Es,a∼ρ(⋅)[(yi−Q(s,a;θi))2](2)

其中，

y i = E s ′ ∼ E [ r + γ max ⁡ a ′ Q ( s ′ , a ′ ; θ i − 1 ) ∣ s , a ] \begin{array} { r } { y _ { i } \; = \; \mathbb { E } _ { s ^ { \prime } \sim \mathcal { E } } \left[ r + \gamma \operatorname* { m a x } _ { a ^ { \prime } } Q ( s ^ { \prime } , a ^ { \prime } ; \theta _ { i - 1 } ) | s , a \right] } \end{array} yi=Es′∼E[r+γmaxa′Q(s′,a′;θi−1)∣s,a]

是第 i i i 次迭代中的目标值 ， ρ ( s , a ) \rho(s, a) ρ(s,a) 是在状态序列 s s s 与动作 a a a 上的一个概率分布，我们称之为行为分布（behaviour distribution） 。在优化损失函数 L i ( θ i ) L_i(\theta_i) Li(θi) 时，使用的是前一次迭代中的参数 θ i − 1 \theta_{i-1} θi−1，并在训练过程中保持不变。需要注意的是，这些目标值 y _ i y\_i y_i 是依赖于网络参数的；这与监督学习不同，在监督学习中，目标在训练开始前就已经确定。

对损失函数关于参数 θ i \theta_i θi 求导，得到梯度表达式如下：

∇ θ i L i ( θ i ) = E s , a ∼ ρ ( ⋅ ) ; s ′ ∼ E [ ( r + γ max ⁡ a ′ Q ( s ′ , a ′ ; θ i − 1 ) − Q ( s , a ; θ i ) ) ∇ θ i Q ( s , a ; θ i ) ] ( 3 ) \begin{array} { r } { \nabla _ { \theta _ { i } } L _ { i } \left( \theta _ { i } \right) = \mathbb { E } _ { s , a \sim \rho ( \cdot ) ; s ^ { \prime } \sim \mathcal { E } } \left[ \left( r + \gamma \operatorname* { m a x } _ { a ^ { \prime } } Q ( s ^ { \prime } , a ^ { \prime } ; \theta _ { i - 1 } ) - Q ( s , a ; \theta _ { i } ) \right) \nabla _ { \theta _ { i } } Q ( s , a ; \theta _ { i } ) \right] } \end{array}\quad(3) ∇θiLi(θi)=Es,a∼ρ(⋅);s′∼E[(r+γmaxa′Q(s′,a′;θi−1)−Q(s,a;θi))∇θiQ(s,a;θi)](3)

与其计算上述期望的完整形式，在实际应用中，通常使用随机梯度下降（SGD）来优化损失函数以提高计算效率。也就是说，如果在每一个时间步更新参数，并且将上述期望替换为从行为分布 ρ \rho ρ 和环境 E E E 中采样得到的单一样本，我们就得到了熟知的 Q-learning 算法 [26]。

请注意，这一算法是模型无关（model-free）的：它直接通过从环境 ${ \\varepsilon }$ 中采样来求解强化学习任务，而不需要显式构建对环境 ε { \varepsilon } ε 的估计。同时，它也是离策略（off-policy）的：尽管学习目标是贪婪策略 a = max ⁡ a Q ( s , a ; θ ) a = \max_a Q(s, a; \theta) a=maxaQ(s,a;θ)，但训练过程中遵循的是某种行为分布，以确保足够的探索。

在实践中，行为分布通常由一个 ε \varepsilon ε-贪婪策略 （ ε \varepsilon ε-greedy strategy）定义：以概率 1 − ε 1 - \varepsilon 1−ε 选择当前估计的最优动作（贪婪策略），以概率 ε \varepsilon ε 随机选择一个动作。

3 相关工作

强化学习中最著名的成功案例之一，或许就是 TD-Gammon：一个通过强化学习和自我对弈训练出来的西洋双陆棋程序，其水平达到了超越人类的程度 [24]。TD-Gammon 使用了类似于 Q-learning 的模型无关（model-free）强化学习算法，并通过一个带有单隐藏层的多层感知机（multi-layer perceptron）来逼近价值函数。

然而，早期对 TD-Gammon 方法的后续尝试并不成功，包括将其应用于国际象棋、围棋和跳棋等游戏。这导致人们普遍认为 TD-Gammon 是一个特例，只能在西洋双陆棋中奏效，可能是因为骰子的随机性有助于探索状态空间，同时也使得该游戏的价值函数相对平滑 [19]。

此外，已有研究表明，将模型无关的强化学习算法 （如 Q-learning）与非线性函数逼近器结合 [25]，或者与离策略学习（off-policy learning）结合 [1]，可能会导致 Q 网络的发散。因此，此后大多数强化学习研究都集中在使用线性函数逼近器上，以获得更好的收敛性保证[25]。

近年来，结合深度学习与强化学习的研究重新受到关注。深度神经网络已被用于估计环境 E E E；受限玻尔兹曼机已被用于估计价值函数 [21]；或估计策略函数 [9]。此外，Q-learning 的发散问题已通过梯度时序差分方法得到部分缓解。这些方法已被证明在使用非线性函数逼近器评估固定策略时是收敛的 [14]；或在使用线性函数逼近器并采用一种受限形式的 Q-learning 来学习控制策略时是收敛的 [15]。然而，这些方法尚未扩展到非线性控制任务。

或许与我们方法最相似的已有工作是神经拟合 Q-learning（Neural Fitted Q-learning，NFQ）[20]。NFQ 使用 RPROP 算法来优化第 2 式中的损失函数序列，并更新 Q 网络的参数。然而，它采用的是批量更新方式，其每次迭代的计算成本与数据集的大小成正比；而我们考虑的是具有固定低计算成本并可扩展到大规模数据集的随机梯度更新方式。NFQ 也已被成功地应用于一些仅使用视觉输入的简单真实控制任务中，这些任务首先使用深度自编码器学习任务的低维表示，然后将 NFQ 应用于该表示空间 [12]。相比之下，我们的方法是端到端的强化学习方法，直接从视觉输入中学习；因此，它可能学到的是对区分动作价值更具相关性的特征。Q-learning 也曾被与经验回放机制和一个简单的神经网络结合使用 [13]，但其起点是低维状态，而非原始视觉输入。

将 Atari 2600 模拟器作为强化学习平台最早由 [3] 引入，该工作使用了带有线性函数逼近器和通用视觉特征的标准强化学习算法。随后，相关结果通过使用更多特征并利用拔河哈希（tug-of-war hashing）将这些特征随机投影到低维空间中而得到改进 [2]。HyperNEAT 进化架构 [8] 也已被应用于 Atari 平台，它为每个不同的游戏分别演化出一个表示该游戏策略的神经网络。在对抗确定性游戏序列反复训练并利用模拟器的重置功能时，这些策略能够利用多个 Atari 游戏中的设计缺陷。

4 深度强化学习

近年来，计算机视觉和语音识别领域的突破依赖于在极大规模训练集上高效训练深度神经网络。最成功的方法是直接从原始输入中训练的，使用基于随机梯度下降的轻量级更新方式。通过向深度神经网络输入足够多的数据，通常可以学得比手工设计特征更优的表示 [11]。这些成功激励了我们对强化学习的研究方法。我们的目标是将强化学习算法与深度神经网络相结合，使其直接作用于 RGB 图像输入，并通过随机梯度更新高效处理训练数据。

Tesauro 的 TD-Gammon 架构为这种方法提供了一个起点。该架构直接利用从策略样本 ( s t , a t , r t , s t + 1 , a t + 1 ) (s_t, a_t, r_t, s_{t+1}, a_{t+1}) (st,at,rt,st+1,at+1)（通过算法与环境的交互获得，或在 backgammon 游戏中通过自对弈获得）来更新估计价值函数的网络参数。由于该方法在 20 年前就已经能够超越人类 backgammon 顶尖选手，我们自然会思考，倘若结合过去二十年的硬件进步、现代的深度神经网络架构以及可扩展的强化学习算法，是否能带来显著的进展。

与 TD-Gammon 及类似的在线方法不同，我们采用了一种称为"经验回放"（experience replay）的技术 [13]，在该方法中，我们将智能体每一步的经历 e t = ( s t , a t , r t , s t + 1 ) e_t = (s_t, a_t, r_t, s_{t+1}) et=(st,at,rt,st+1) 存储在数据集 D = e 1 , ... , e N D = {e_1, \dots, e_N} D=e1,...,eN 中，这些经历跨多个 episode 聚合组成一个回放记忆池。在算法的内循环中，我们从该记忆池中随机抽取样本 e ∼ D e \sim D e∼D，并对这些经历执行 Q-learning 更新或 minibatch 更新。在完成经验回放之后，智能体根据 ϵ \epsilon ϵ-greedy 策略选择并执行一个动作。由于使用任意长度的历史作为神经网络的输入存在困难，我们的 Q 函数作用于由函数 ϕ \phi ϕ 生成的固定长度的历史表示上。完整算法（我们称之为深度 Q-learning）在算法 1 中给出。

这种方法相比标准的在线 Q-learning [23] 有若干优点。首先，每一步经历在训练过程中可能被用于多次权重更新，这使得数据利用效率更高。

温馨提示：

阅读全文请访问"AI深语解构 " 用深度强化学习玩Atari游戏