【图论】图的定义与一些常用术语

【图论】图的定义

图论编辑器1：https://csacademy.com/app/graph_editor/

图论编辑器2：https://graphonline.top/ch/

图（graph）由节点（node）和边（edge）组成。其中，节点集合记为 V V V，边集合记为 E E E 。每条边连接两个节点，某些图的边可能具有方向性。集合元素的数量用该集合的绝对值来表示。

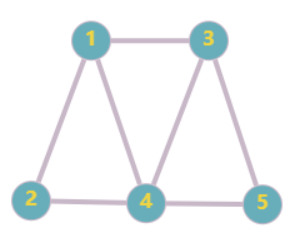
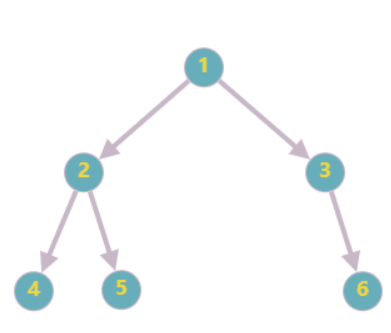
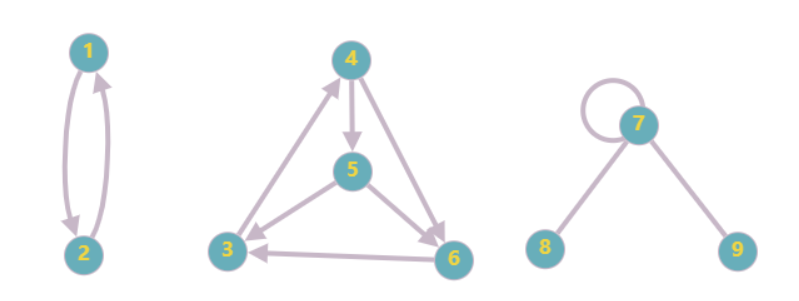
通过对比可以看出，图比树具有更大的灵活性。例如，树结构要求子节点不能与父节点直接相连且禁止横向连接，而图不仅允许任意节点间自由连接，还支持自环和方向定义。可以说树是图论中的一种特殊结构，或者说是一种受到严格限制的图。

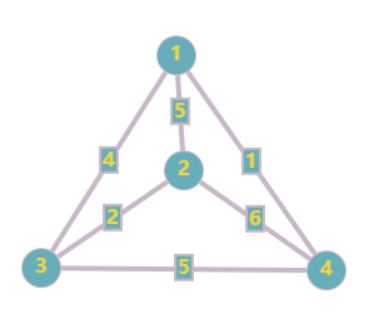
对于一些图的边会给出一个数值，这个值叫做边权（weight）。它可以表示为距离、过路费、障碍数量等各种各样的数值。

有向图是指有方向的图，只能沿着箭头方向移动，不能走回头路；而无向图则可以自由通行

从一点开始，中间经历不重复 的边到另一个点中间的路叫路径（path）

从一点开始，中间经历可重复 的边到另一个点中间的路叫途径（way 或 walk）

环：从一个点到它本身，序列长度至少为 2 2 2 的路径

重边：允许两个点之间有多条边

自环：允许边自己连向自己

度：用于无向图 ，与自己连接的边的条数

入度：用于有向图 ，以自己为终点的边的条数

出度：用于有向图，以自己为起点的边的条数

点 u u u 和点 v v v 连通：是否存在从点 u u u 到点 v v v 的路径

联通分量：与一个点连通的所有点构成的集合

把有向边的方向忽略得到无向图，对应这个无向图中的连通、连通分量和连通图就是弱连通、弱连通分量和弱连通图；在有向图中，如果两个顶点之间至少存在一条路径，则称这两个顶点是强连通的。如果一个有向图中的任意两个顶点都是强连通的，则称该图为强连通图。对于非强连通图，其极大强连通子图被称为强连通分量

图的稀疏性与稠密性主要取决于图中边的数量相对于顶点数量的密度。如果图中 ∣ E ∣ ≪ ∣ V ∣ 2 |E| \ll |V|^2 ∣E∣≪∣V∣2，则这个图为稀疏图；若 ∣ E ∣ ≈ ∣ V ∣ 2 |E| \approx |V|^2 ∣E∣≈∣V∣2，则此图为稠密图

这个用于字符迷宫上，例如对于任意一个位置，你可以上下左右移动，这就叫做四联通；如果你可以八方移动，就叫八联通

在编程实现中，一般会定义方向数组。

四方向数组：

cpp 复制代码

const int DX[4] = {0, 1, 0, -1};
const int DY[4] = {1, 0, -1, 0};

八方向数组：

cpp 复制代码

const int DX[8] = {-1, 1, 0, 0, -1, -1, 1, 1};
const int DY[8] = {0, 0, -1, 1, -1, 1, -1, 1};