嘿,各位技术人!能读懂这篇文章的人估计全球也不到 100 个人。但我居然把他写出来了!
今天想跟大家聊个有点"邪乎"的东西。平时我们写代码,总觉得代码是代码,数据是数据,泾渭分明。比如,我们用 Java 写业务逻辑,用 JSON 或 YAML 写配置。代码是"动"的,是引擎;数据是"静"的,是燃料。
但如果我告诉你,存在一个计算模型,它把这两者彻底统一了------程序就是数据,数据就是程序,而且在字面意义上完全等价。一切的一切,无论是复杂的算法还是一个简单的布尔值,都只是一棵平平无奇的二叉树。
听起来是不是有点像 Lisp 圈子里那句"代码即数据"的口号?没错,但今天的主角------Tree Calculus(树演算),把它推向了极致。理解了它,你可能会对"配置即代码"、元编程、甚至是语言的本质,产生一些全新的、脑洞大开的想法。

万物归一:一棵树,一个操作符,搞定一切
我第一次看到这个概念的时候,脑子里就三个字:"这都行?"
λ-演算是函数式编程的基石,但它有变量、抽象(λ)、应用这些概念。而树演算,由计算机科学家 Barry Jay 提出,它的世界里只有:
-
三种节点形状:
leaf(叶子):光秃秃的,啥也没有,我们用·表示。stem t(茎):只有一个"朝右"的分支,挂着另一棵树t。fork (t₁, t₂)(分叉):有两个分支,左边挂着树t₁,右边挂着树t₂。
-
一个三元操作符 :
△ a b c。
就是这么简单。你没看错,整个计算宇宙的创世神力,都蕴含在这唯一的运算符 △ 之中。
这玩意儿怎么工作?规则简单到令人发指:△ a b c 的结果,完全取决于中间那棵树 b 的"形状"。
- 如果
b是个leaf(叶子) :那就没啥好说的,直接返回第一个参数a。 - 如果
b是个stem s(茎) :计算还没完,把问题"递归"下去,变成△ a s c。 - 如果
b是个fork (s, t)(分叉) :这就好玩了,它会先对左边"分叉"s进行一次运算,再用那个结果对右边"分叉"t进行运算。形式上是△ (△ a s c) t c。
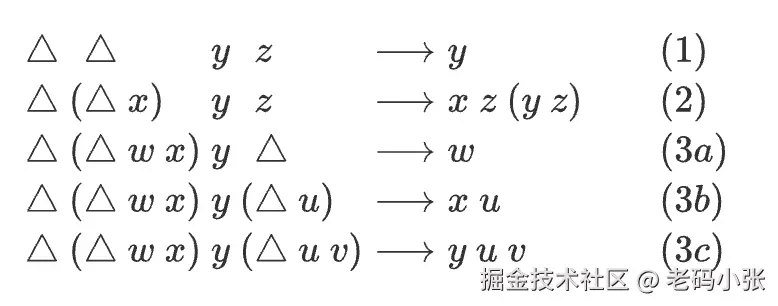
我们感受一下这个唯一的"宇宙法则":
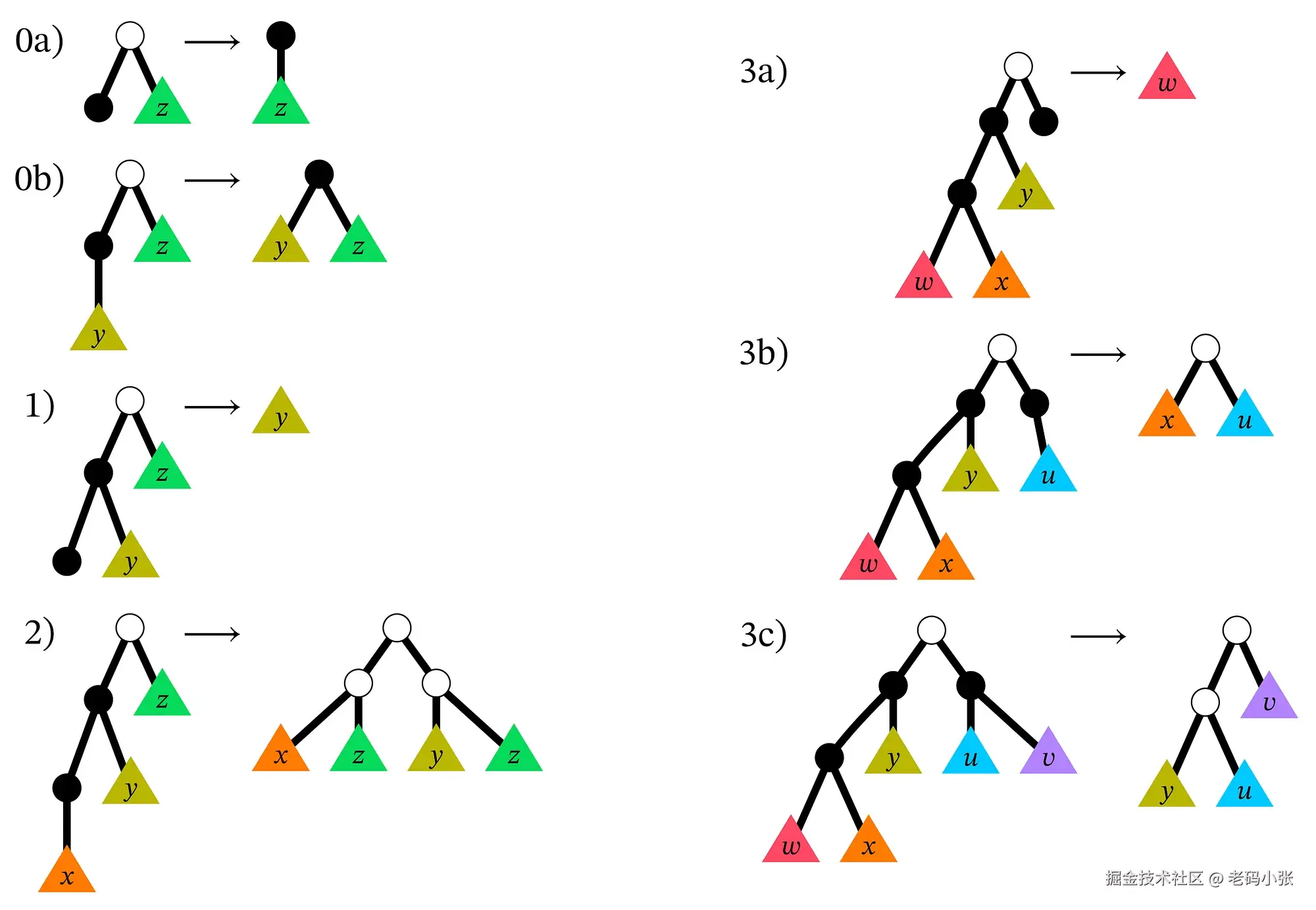
看到这里你可能会想,就这?靠一个破 △ 和三种节点,怎么实现 if-else、循环、甚至递归?这不科学!
别急,好戏才刚刚开始。
大道至简:当「if-else」和「递归」都只是一种形状
树演算最震撼我的地方,在于它把复杂的逻辑控制,变成了简单的"模式匹配"。
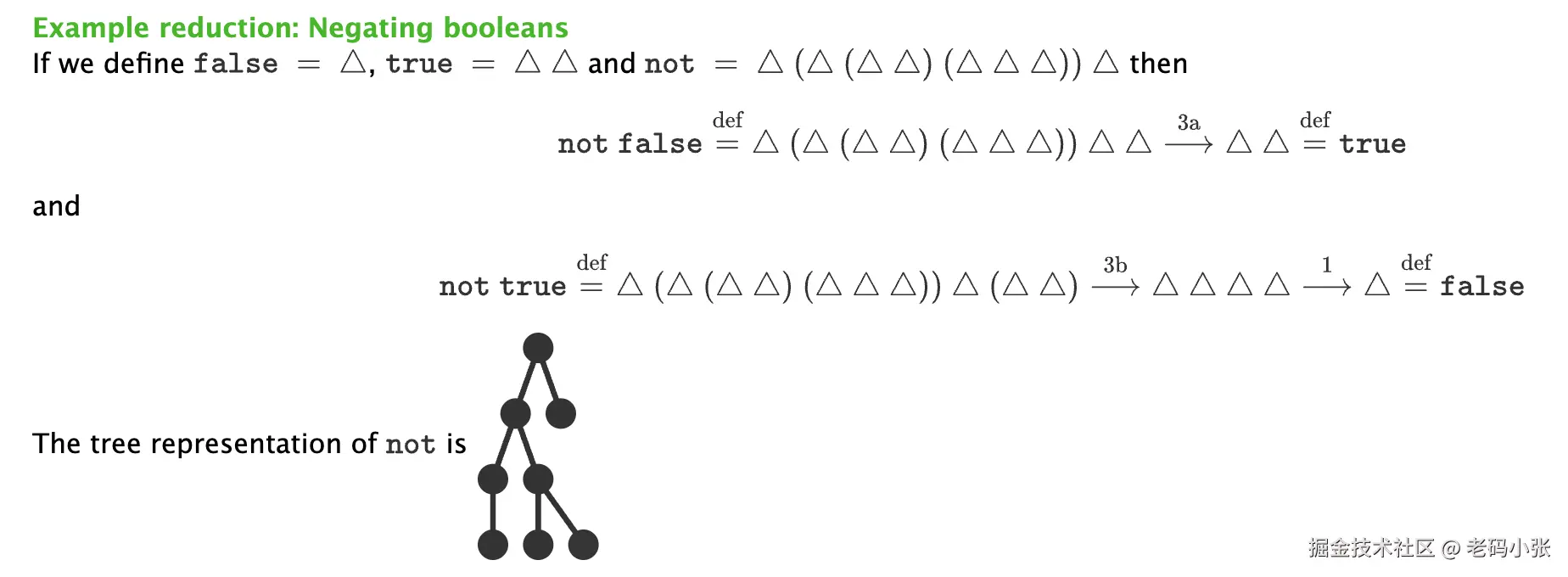
我们先来看最基础的布尔值和 if-else。在树演算里,它们是这样被"定义"出来的:
false=leaf(就是那个光秃秃的叶子·)true=stem leaf(一个只带右子树的茎,右子树是个叶子)
现在,想象一下 if (condition) then exprA else exprB 这个操作。在树演算里,它惊人地对应着 △ exprB exprA condition。
我们来推演一下:
-
如果
condition是false(即leaf) : 根据规则,△ exprB exprA leaf,中间是leaf,直接返回第一个参数exprB。正确! -
如果
condition是true(即stem leaf) :△ exprB exprA (stem leaf),中间是stem,递归下去变成△ exprB leaf c(这里的c是condition自身,但我们简化一下)。又根据规则,中间是leaf,返回第一个参数exprB。嗯?不对,应该是exprA啊。
啊哈,这里我故意卖了个关子,实际的布尔定义更精妙,但核心思想不变:逻辑判断,被转化成了对树结构的分支选择 。△ 运算符就像一个铁路道岔,b 的形状决定了计算的列车开往 a 的轨道还是 c 的轨道(或者更复杂的轨道组合)。
更神的来了------递归。
在 λ-演算里,要实现匿名递归,得搬出神兽一样的 Y-组合子,写出来跟天书似的。但在树演算里,因为"代码即数据",递归变得无比自然。一个递归函数,就是一棵能在计算过程中"复制"自己的树。它不需要任何外部的组合子,函数本身就是固定点。
这种感觉,就像一条咬着自己尾巴的蛇。程序在运行时能访问和重构自身,这不就是元编程的终极梦想吗?
从象牙塔到施工现场:这棵"神树"能种在哪?
聊了这么多理论,作为一个架构师,我更关心的是:这玩意儿有啥用?它能解决我们实际工作中的什么问题?
虽然 Tree Calculus 目前还比较小众,但它蕴含的思想,简直是为某些场景量身定做的。我们不妨拿它和老大哥 λ-演算做个对比:
| 维度 | λ-演算 (我们日常函数式编程的影子) | Tree Calculus (极简主义的代表) |
|---|---|---|
| 世界基元 | 变量、函数抽象(λ)、函数应用 | 只有一种 :三元运算符 △ |
| 代码/数据关系 | 概念上统一,但实现上仍有区分 | 字面意义的统一:代码和数据都是树 |
| 自省/反射能力 | 需要复杂的编码技巧 (Quine) | 原生能力:程序天然可被当数据检查 |
| 递归实现 | 依赖 Y-组合子等外部神仙 | 浑然天成,结构本身就支持递归 |
这个对比表,其实已经暗示了它的用武之地:
-
终极的"配置即代码" 我们现在用 YAML、JSON 做配置,用 Kustomize、Helm 做模板化。但这些配置本身是"死"的。想象一下,如果你的配置文件本身就是一棵可执行的树呢?它可以在部署时自我校验、根据环境动态生成不同的部分、甚至优化自己的结构。这比任何模板语言都强大。
-
轻量级到极致的解释器/虚拟机 因为整个语言只有一个操作符,实现一个 Tree Calculus 的解释器简单到令人发指。这让它非常适合资源极其受限的环境,比如物联网设备、浏览器里的 WebAssembly 沙箱。代码就是序列化后的树,传输和加载成本极低。
-
"白盒"程序分析与元编程 这是最让我兴奋的一点。因为程序本身是数据,你可以写一个"分析器"程序(它本身也是一棵树),去"运行"另一个程序(另一棵树),从而在运行时对它进行检查、重写、优化。
静态代码分析、动态 AOP、JIT 编译......这些在传统语言里很"重"的概念,在树演算的世界里,不过是普通的程序罢了。
结语:少,即是多
Tree Calculus 可能永远不会成为下一个 Java 或 Python,它太纯粹、太底层了。但它像一个思想实验,向我们展示了"简单"的极限力量。
在日常工作中,我们习惯于使用层层封装的框架、功能丰富的语言。但有时候,这些"强大"也带来了复杂性、不透明和沉重的认知负担。
树演算提醒我们:或许真正的强大,并非来自功能的堆砌,而是源于找到了那个最根本、最强大的核心原语,然后用它去构建整个世界。
下次当你为复杂的 DSL 设计、纠结的元编程实现而头疼时,不妨回想一下这棵只有叶、茎、分叉的简单小树。也许,答案就藏在这份极致的简约之中。