目录
1.程序功能描述
椭圆曲线密码学(Elliptic Curve Cryptography, ECC)作为现代公钥密码学的重要分支,以其在相同安全级别下密钥更短、计算效率更高的优势,成为资源受限环境(如移动设备、物联网)中数据加密的理想选择。将ECC应用于图像加解密领域,不仅能保护图像内容的机密性,还能充分利用图像数据的二维特性和ECC的数学特性,设计出高效且安全的加密方案。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
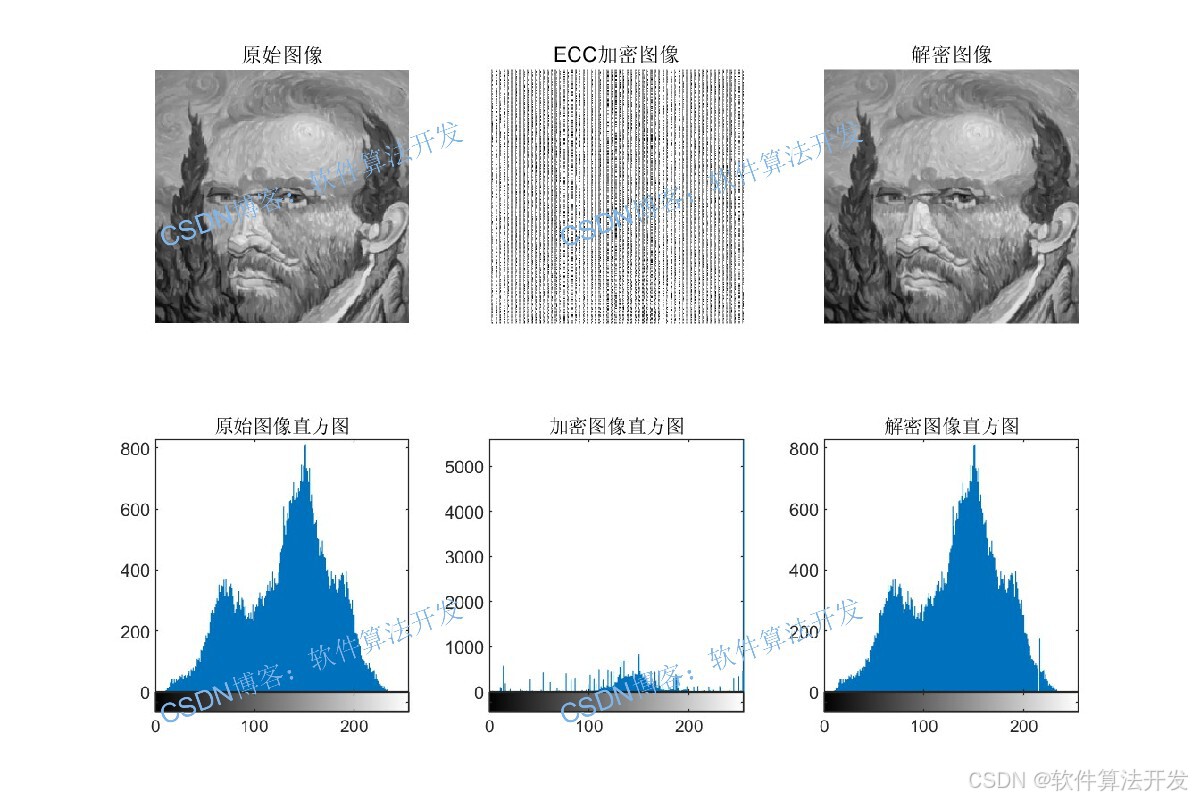
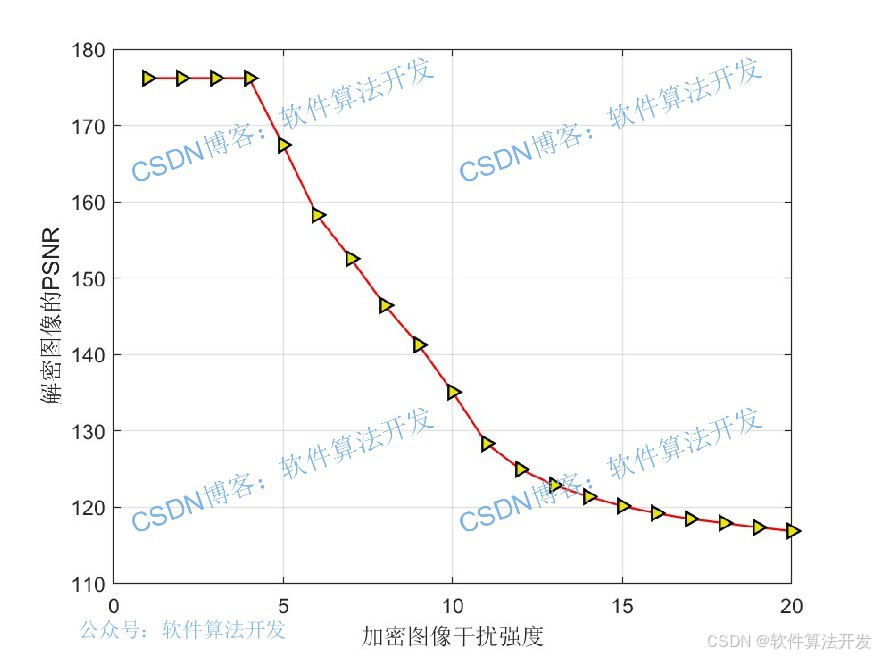
3.部分程序
% 生成加密所需的基点和参数
aphn = func_primroot(p); % 获取原根
Xm1 = func_mult([d(1),d(2)],aphn,a,b,p); % 计算基点的标量乘法
Xm2 = func_mult([d(1),d(2)],k,a,b,p); % 计算基点的标量乘法
% 图像加密过程
for i=1:m
for j=1:n
m1 = x(i,j); % 获取当前像素值
c = func_Elliptic(m1,a,b,p,K); % 将像素值映射到椭圆曲线上
% 执行椭圆曲线上的加密操作
Xm3= func_add([c(1),c(2)],func_mult([Xm1(1),Xm1(2)],k,a,b,p),a,b,p);
% 存储加密结果(每个像素转换为椭圆曲线上的两个点)
jm(l) = Xm2(1);
jm(l+1)= Xm2(2);
jm(l+2)= Xm3(1);
jm(l+3)= Xm3(2);
l=l+4;
end
end
1064.算法理论概述
ECC的安全性基于椭圆曲线离散对数问题(ECDLP):给定椭圆曲线上的点P和Q,找到整数k使得Q=kP在计算上是困难的。目前没有已知的多项式时间算法能解决ECDLP,这使得ECC在较小密钥长度下提供与RSA、DSA等传统公钥算法相当的安全性。例如:
160位ECC密钥 ≈ 1024位RSA密钥
256位ECC密钥 ≈ 3072位RSA密钥
椭圆曲线上的点运算定义如下:

传统图像加密方法(如AES、DES)通常将图像视为一维数据流处理,忽略了图像的二维结构和像素间的相关性。基于ECC的图像加密算法则结合了ECC的数学特性和图像的空间特性,主要通过以下方式实现:
像素值变换:利用ECC点运算对像素值进行非线性变换;
像素位置置乱:基于ECC生成混沌序列,对像素位置进行重排;
密钥生成与管理:使用ECC生成公钥/私钥对,实现安全的密钥交换和管理。
基于ECC的图像加密算法通常包含以下核心模块:
密钥生成:基于ECC生成公钥 / 私钥对;
混沌序列生成:利用ECC点运算生成伪随机序列,用于像素置乱和值变换;
像素置乱:改变像素的空间位置,打乱图像的视觉特征;
像素值加密:对置乱后的像素值进行变换,使其统计特性接近噪声;
解密过程:逆序执行加密步骤,恢复原始图像。
基于ECC的图像加解密算法充分利用了椭圆曲线密码学的数学特性和图像数据的二维结构,通过像素置乱和值变换实现了高效且安全的图像加密。
5.参考文献
1\]胡滟.ECC加解密技术中算法优化研究与实现\[D\].云南大学,2011.DOI:CNKI:CDMD:2.2010.265235. \[2\]苏斌.一种ECC\\\\RSA加解密协处理器:CN200610167380.3\[P\].CN100583757C\[2025-07-21\].DOI:CN100583757 C. \[3\]何泽.基于RSA/ECC算法的可配置加解密协处理器\[D\].西安电子科技大学\[2025-07-21\].DOI:CNKI:CDMD:2.1019.003284. ## 6.完整程序 **VVV**