3.1 非线性规划模型
3.1.1 非线性规划的定义
当目标函数或约束条件中包含非线性函数时,就称这种规划问题为非线性规划问题。非线性规划目前尚未有适用于各类问题的通用方法,各种方法都有自己的适用范围。
非线性规划的一般形式:
min f(x)s. t. {hj(x)≤0,j=1,...,qgi(x)=0,i=1,...,pmin\,f(x)\\ s.\, t. \, \left\{\begin{matrix} h_j(x) \le 0,j=1,...,q \\ g_i(x)=0,i=1,...,p \end{matrix} \right.minf(x)s.t.{hj(x)≤0,j=1,...,qgi(x)=0,i=1,...,p
式中:x=[x1,...,xn]Tx=[x_1,...,x_n]^Tx=[x1,...,xn]T为决策变量;fff为目标函数,gig_igi和hjh_jhj为约束函数(等式约束和不等式约束)。
3.1.2 非线性规划的Matlab解法
Matlab中非线性规划的标准数学模型为:
min f(x)s. t. {A⋅x≤bAeq⋅x=beqc(x)≤0ceq(x)=0lb≤x≤ubmin\,f(x)\\ s.\, t. \, \left\{\begin{matrix} A \cdot x \le b \\ Aeq \cdot x=beq\\ c(x) \le 0\\ ceq(x)=0 \\ lb \le x \le ub \end{matrix} \right.minf(x)s.t.⎩ ⎨ ⎧A⋅x≤bAeq⋅x=beqc(x)≤0ceq(x)=0lb≤x≤ub
式中:f(x)f(x)f(x)为标量函数;A,b,Aeq,beq,lb,ubA,b,Aeq,beq,lb,ubA,b,Aeq,beq,lb,ub为对应维数的矩阵和向量;c(x),ceq(x)c(x),ceq(x)c(x),ceq(x)为非线性向量函数。
matlab
[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)其中:
xxx和fvalfvalfval分别返回决策变量的值和目标函数的值;
fun是定义的函数f(x)f(x)f(x);x0x0x0是初值;
A,b,Aeq,beqA,b,Aeq,beqA,b,Aeq,beq定义了线性约束,若没有线性约束,则为[ ];
lb,ublb,ublb,ub为下界和上界,若没有上下界,则为[ ];也可以写为lb为-inf,ub为inf;
nonlcon是M文件定义的非线性向量函数c(x),ceq(x)c(x),ceq(x)c(x),ceq(x);
options定义了优化参数,可以使用Matlab的默认设置。
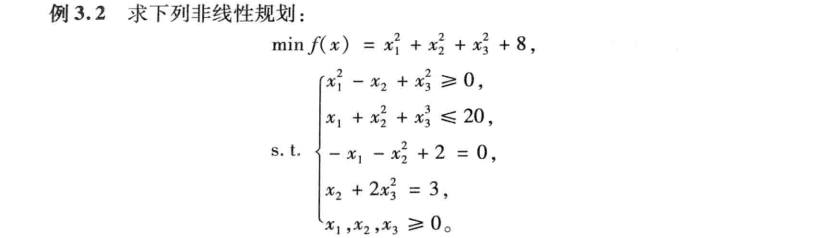
(1)编写M函数定义目标函数和非线性约束:
matlab
function f=fun1(x)
f=sum(x.^2)+8;
matlab
function [g,h]=fun2(x)
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3];%非线性等式约束(2)编写主程序:
matlab
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')
matlab
补充:
rand - 均匀分布的随机数
此 MATLAB 函数 返回从区间 (0,1) 的均匀分布中得到的随机标量。
X = rand
X = rand(n)
X = rand(sz1,...,szN)
X = rand(sz)
X = rand(___,typename)
X = rand(___,"like",p)
X = rand(s,___)
输入参数
n - 方阵的大小
整数值
sz1,...,szN - 每个维度的大小(作为单独参数)
整数值
sz - 每个维度的大小(作为行向量)
整数值
typename - 要创建的数据类型(类)
"double" (默认值) | "single"
p - 要创建的数组的原型
数值数组
s - 随机数流
RandStream 对象3.2 无约束问题的Matlab求解
3.2.1 无约束极值问题的符号解

matlab
clc,clear
syms x y
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f); %求一阶偏导数
d2f=jacobian(df); %求二阶偏导数
[xx,yy]=solve(df) %求驻点
for i=1:length(xx)
a=subs(d2f,{x,y},{xx(i),yy(i)}); % 代入驻点计算
b=eig(a); %求Hessian矩阵特征值
f=subs(f,{x,y},{xx(i),yy(i)});
if all(b>0)
fprint('(%f,%f)是极小值点,极小值为%f\n',xx(i),yy(i),f);
else if all(b<0)
fprint('(%f,%f)是极大值点,极大值为%f\n',xx(i),yy(i),f);
else if any(b>0) & any(b<0)
fprintf('(%f,%f)不是极值点\n',xx(i),yy(i));
else
fprintf('无法判断(%f,%f)是不是极值点\n',xx(i),yy(i));
end
end
matlab
补充:
sym/jacobian - Jacobian matrix
This MATLAB function computes the Jacobian matrix of f with respect to v.
jacobian(f,v)
输入参数
f - Scalar or vector function
symbolic expression | symbolic function | symbolic vector
v - Vector of variables or functions with respect to which you compute Jacobian
symbolic variable | symbolic function | symbolic vector
-----------------------------------------------------
subs - Symbolic substitution
This MATLAB function returns a copy of s, replacing all occurrences of old with new, and then evaluates s.
snew = subs(s,old,new)
snew = subs(s,new)
snew = subs(s)
sMnew = subs(sM,oldM,newM)
sMnew = subs(sM,newM)
输入参数
s - Symbolic input
symbolic scalar variable | symbolic expression | symbolic equation | symbolic function | symbolic array | symbolic matrix | structure
old - Scalar variable to substitute
symbolic scalar variable | symbolic function | symbolic expression | symbolic array | cell array
new - New value
number | symbolic number | symbolic scalar variable | symbolic function | symbolic expression | symbolic array | structure | cell array
sM - Symbolic input
symbolic matrix variable | symbolic matrix function | symbolic expression | symbolic equation | symbolic condition
oldM - Matrix variable or function to substitute
symbolic matrix variable | symbolic matrix function | symbolic expression | cell array
newM - New value
number | symbolic number | symbolic matrix variable | symbolic matrix function | symbolic expression | symbolic array | cell arra
-----------------------------------------------------
eig - 特征值和特征向量
此 MATLAB 函数 返回一个列向量,其中包含方阵 A 的特征值。
e = eig(A)
[V,D] = eig(A)
[V,D,W] = eig(A)
e = eig(A,B)
[V,D] = eig(A,B)
[V,D,W] = eig(A,B)
[___] = eig(A,balanceOption)
[___] = eig(A,B,algorithm)
[___] = eig(___,outputForm)
输入参数
A - 输入矩阵
方阵
B - 广义特征值问题输入矩阵
方阵
balanceOption - 均衡选项
'balance' (默认值) | 'nobalance'
algorithm - 广义特征值算法
'chol' | 'qz'
outputForm - 特征值的输出格式
'vector' | 'matrix'
输出参数
e - 特征值(以向量的形式返回)
列向量
V - 右特征向量
方阵
D - 特征值(以矩阵的形式返回)
对角矩阵
W - 左特征向量
方阵
-----------------------------------------------------
any - 确定是否有任何数组元素非零
此 MATLAB 函数 沿着大小不等于 1 的数组 A 的第一维测试所有元素为非零数字还是逻辑值 1(true)。实际上,any 是逻辑 OR 运算符的原生扩展。 如果 A 为向量,当 A 的任何元素是非零数字或逻辑 1 (true) 时,B = any(A) 返回逻辑 1,当所有元素都为零时,返回逻辑 0(false)。 如果 A 为非空非向量矩阵,B = any(A) 将 A 的各列视为向量,返回包含逻辑 1和 0 的行向量。 如果 A 为 0×0 空矩阵,any(A) 返回逻辑 0 (false)。 如果 A 为多维数组,则 any(A) 沿第一个非单一维度运算并返回逻辑值数组。此维的大小将变为 1,而所有其他维的大小保持不变。
B = any(A)
B = any(A,'all')
B = any(A,dim)
B = any(A,vecdim)
输入参数
A - 输入数组
标量 | 向量 | 矩阵 | 多维数组
dim - 沿其运算的维度
正整数标量
vecdim - 维度向量
正整数向量
输出参数
B - 逻辑数组
标量 | 向量 | 矩阵 | 多维数组 3.2.2无约束极值问题的数值解
在Matlab中,用于求解无约束极小值问题的函数有fminunc和fminsearch。
minx f(x)\min_x \, f(x)xminf(x)
xxx为标量或向量。
matlab
[x,fval]=fminsearch(fun,x0,options)xxx为极小值点,fval是极小值。fun是M函数,当只有一个返回值时,返回值是函数f(x)f(x)f(x);当有两个返回值时,第二个返回值是f(x)f(x)f(x)的梯度向量;当有三个返回值时,第三个返回值是f(x)f(x)f(x)的二阶导数(Hessian矩阵)。x0为初值,options为优化参数。
matlab
[x,fval]=fminsearch(fun,x0,options)
%fminsearch只能求初值附近的一个极小值点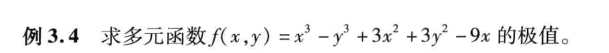
matlab
clc,clear
f=@(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1); %定义匿名函数
g=@(x) -f(x);
[xy1,fval1]=fminunc(f,rand(2,1)); %求极小值点
[xy2,fval2]=fminsearch(g,rand(2,1)); %求极大值点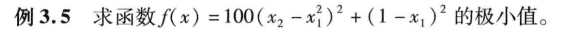
matlab
%使用梯度
%M函数:
function [f,g]=fun(x)
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
g=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)]; %g返回梯度向量
%主程序:
options=optimset('GradObj','on');
[x,y]=fminunc('fun',rand(1,2),options)
matlab
%使用二阶导数
%M函数:
function [f,df,d2f]=fun(x)
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
df=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)];
d2f=[-400*x(2)+1200*x(1)^2+2,-400*x(1),-400*x(1),200];
%主程序:
options=optimset('GradObj','on','Hessian','on');
[x,y]=fminunc('fun',rand(1,2),options)3.2.3 求函数零点和方程组的解
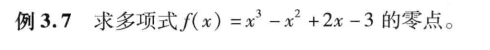
matlab
%roots
clc,clear
a=[1,-1,2,-3]; %多项式系数定义
x0=roots(a)
%----------------------------------------------------
roots - 多项式根
此 MATLAB 函数 以列向量的形式返回 p 表示的多项式的根。输入 p 是一个包含 n+1 多项式系数的向量,以 xn 系数开头。0 系数表示方程中不存在的中间幂。例如:p = [3 2 -2] 表示多项式 3x2+2x−2。
r = roots(p)
输入参数
p - 多项式系数
向量
matlab
%符号求解
syms x
x0=solve(x^3-x^2+2*x-3) %求函数零点的符号解
%----------------------------------------------------
optim.problemdef.OptimizationProblem/solve - 求解优化问题或方程问题 使用 solve 来求优化问题或方程问题的解。
sol = solve(prob)
sol = solve(prob,x0)
输入参数
prob - 优化问题或方程问题
OptimizationProblem 对象 |EquationProblem 对象
x0 - 初始点
结构体 | OptimizationValues 对象的向量
输出参数
sol - 解
结构体 | OptimizationValues 向量
matlab
%求数值解
y=@(x) x^3-x^2+2*x-3;
x=fsolve(y,rand) %只能求初值附近的一个零点
%----------------------------------------------------
fsolve - 对非线性方程组求解
非线性方程组求解器
输入参数
fun - 要求解的非线性方程
函数句柄 | 函数名称
x0 - 初始点
实数向量 | 实数数组
x = fsolve(fun,x0)
输出参数
x - 解
实数向量 | 实数数组3.3 约束极值问题
求解约束极值问题通常使用以下优化:
- 将约束问题转化为无约束问题;
- 将非线性规划问题转化为线性规划问题;
- 复杂问题转化为简单问题。
3.3.1 二次规划
定义:若非线性规划的目标函数值为自变量x的二次函数,约束条件是线性的,则称为二次规划。
Matlab中的二次规划的数学模型为:
min1/2xTHx+fTxs. t.{A⋅x≤b,Aeq⋅x=beq,lb≤x≤ubmin \quad 1/2x^THx+f^Tx\\ s. \, t. \left\{\begin{matrix} A \cdot x \le b,\\ Aeq \cdot x = beq,\\ lb \le x \le ub \end{matrix}\right.min1/2xTHx+fTxs.t.⎩ ⎨ ⎧A⋅x≤b,Aeq⋅x=beq,lb≤x≤ub
式中,HHH为实对称矩阵;f,b,beq,lb,ubf,b,beq,lb,ubf,b,beq,lb,ub为列向量;A,AeqA,AeqA,Aeq为相应维数的矩阵。
matlab
[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)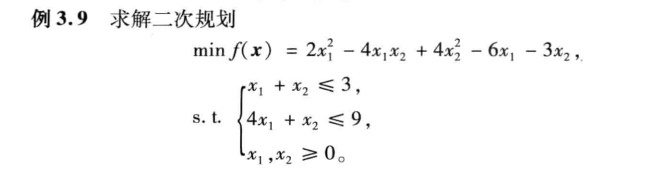
matlab
h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,fval]=quadprog(h,f,a,b,[],[],zeros(2,1))3.3.2 罚函数法
罚函数法可以将非线性规划问题转化为无约束极值问题。
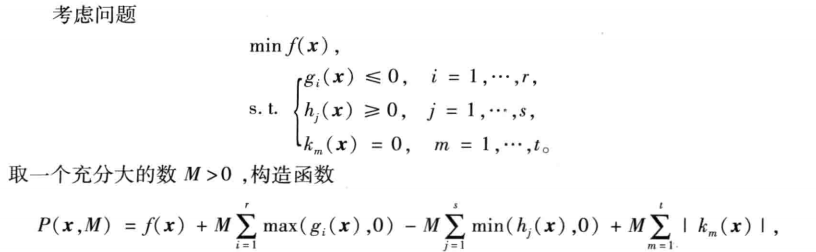

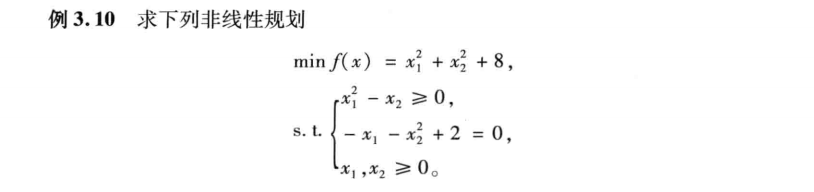
matlab
%定义增广目标函数的M文件:
function g=fun1(x)
M=50000;
f=x(1)^2+x(2)^2+8;
g=f-M*min(x(1),0)-M*min(x(2),0)-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
%利用矩阵运算:
%g=f-M*sum(min([x';zeros(1,2)]))-M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);
%求解:
[x,y]=fminsearch('fun1',rand(2,1))由于是非线性问题,很难求得全局最优解,只能求得一个局部最优解,且每次的运行结果都不一样。
3.3.3 Matlab求约束极值问题
- fminbnd
求解单变量非线性函数在区间的极小值:
minxf(x),x∈[x1,x2]\min_x f(x),x \in [x_1,x_2]xminf(x),x∈[x1,x2]
matlab
[x,fval]=fmibnd(fun,x1,x2,options)- fseminf
求解:
minf(x)s. t. {A⋅x≤b,Aeq⋅x=beq,lb≤x≤ub,c(x)≤0,ceq(x)=0,Ki(x,wi)≤0,1≤i≤n.min f(x)\\ s. \, t. \, \left\{\begin{matrix} A \cdot x \le b,\\ Aeq \cdot x=beq,\\ lb \le x \le ub,\\ c(x) \le 0,\\ ceq(x) = 0,\\ K_i(x,w_i) \le 0,1 \le i \le n. \end{matrix}\right.minf(x)s.t.⎩ ⎨ ⎧A⋅x≤b,Aeq⋅x=beq,lb≤x≤ub,c(x)≤0,ceq(x)=0,Ki(x,wi)≤0,1≤i≤n.
其中,Ki(x,wi)K_i(x,w_i)Ki(x,wi)为标量函数,wiw_iwi为附加变量。
matlab
[x,fval]=fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub)其中:fun定义目标函数;x0为初值;ntheta是半无穷约束Ki(x,wi)K_i(x,w_i)Ki(x,wi)的个数;函数seminfcon由于定义非线性不等式约束c(x)c(x)c(x)、非线性等式约束ceq(x)ceq(x)ceq(x)和半无穷约束Ki(x,wi)K_i(x,w_i)Ki(x,wi)的函数,函数seminfcon有两个参量x和s,s是推荐的取样步长,可以不使用。
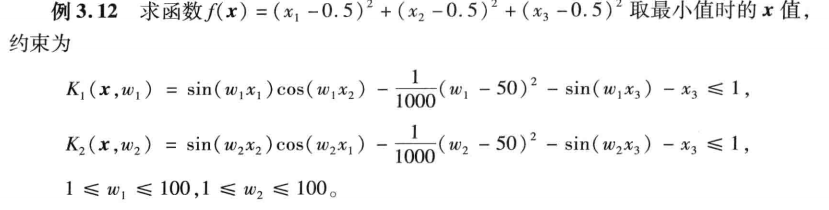
matlab
%定义目标函数:
function f=fun1(x,s)
f=sum((x-0.5).^2);
%定义约束条件:
function [c,ceq,k1,k2,s]=fun2(x,s)
c=[];ceq=[];
if isnan(s(1,1))
s=[0.2,0;0.2,0];
end
w1=1:s(1,1):100; %取样
w2=1:s(2,1):100;
k1=sin(w1*x(1)).*cos(w1*x(2))-1/1000*(w1-50).^2-sin(w1*x(3))-x(3)-1;
k2=sin(w2*x(2)).*cos(w2*x(1))-1/1000*(w2-50).^2-sin(w2*x(3))-x(3)-1;
plot(w1,l1,'-',w2,k2,'+'); %画约束的图形
%调用fseminf:
x0=[0.5;0.2;0.3];
[x,y]=fseminf(@ fun1,x0,2,@ fun2)- fminimax
求解:
minxmaxiFi(x)s. t. {A⋅x≤b,Aeq⋅x=beq,c(x)≤0,ceq(x)=0,lb≤x≤ub,\min_x \max_i F_i(x)\\ s. \, t. \, \left\{\begin{matrix} A \cdot x \le b,\\ Aeq \cdot x=beq,\\ c(x) \le 0,\\ ceq(x) =0,\\ lb \le x \le ub,\\ \end{matrix}\right.xminimaxFi(x)s.t.⎩ ⎨ ⎧A⋅x≤b,Aeq⋅x=beq,c(x)≤0,ceq(x)=0,lb≤x≤ub,
matlab
[x.fval]=fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)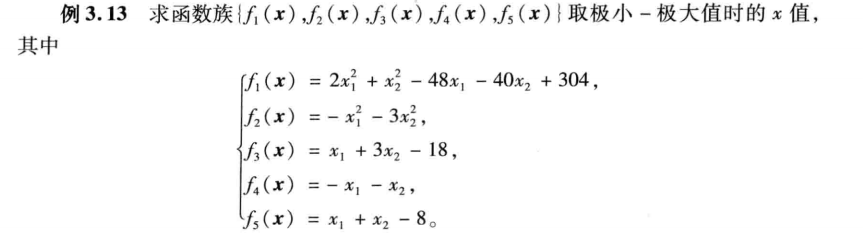
matlab
%定义目标函数
function f=fun1(x)
f=[2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304
-x(1)^2-3*x(2)^2
x(1)+3*x(2)-18
-x(1)-x(2)
x(1)+x(2)-8];
%调用fminimax
[x,y]=fminimax(@ fun1,rand(2,1))