傅里叶转换(机器视觉方向)

傅里叶转换(机器视觉)

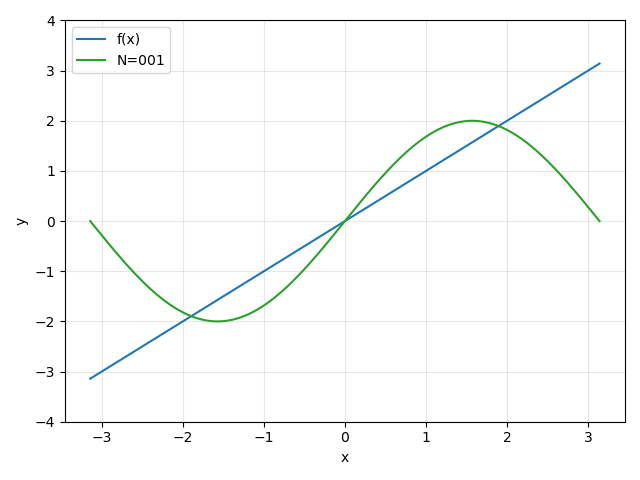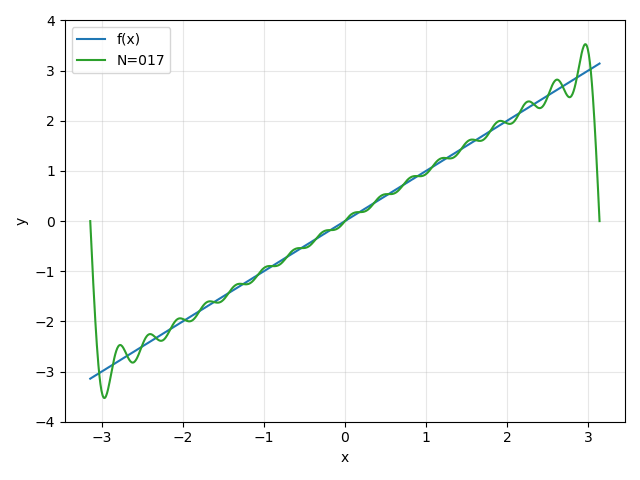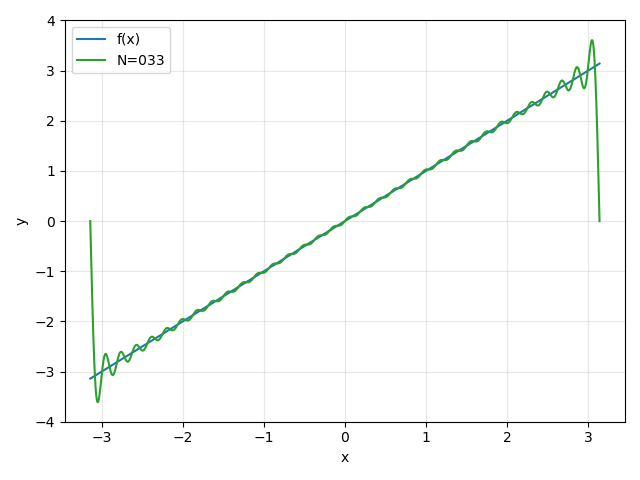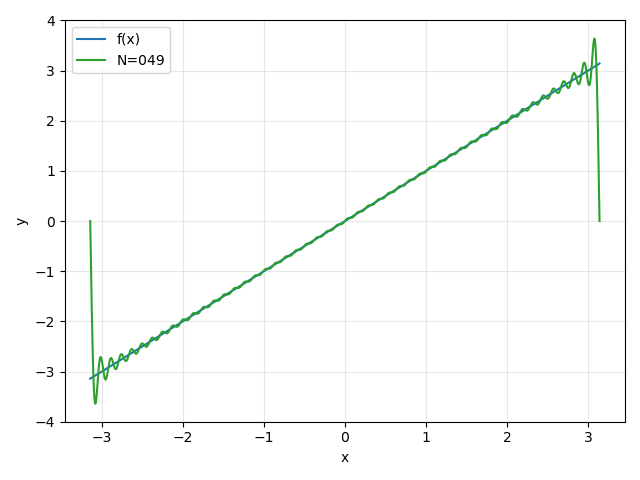
"傅里叶细分"在机器视觉中主要涵盖以下核心方向：

• 滤波增强： 低通、高通、带通/阻、同态滤波。
• 纹理与形状分析： 频谱特征、傅里叶描述子。
• 图像配准： 相位相关法（平移）、对数-极坐标/傅里叶-梅林（旋转缩放）。
• 高效计算： 频域卷积/相关（大核）。
• 压缩基础： 能量集中、变换编码原理。
• 图像重建： CT重建（投影切片定理）。
• 视频分析： 三维傅里叶变换、时空频谱。
• 光学应用： 光学傅里叶变换、光学相关。

傅里叶转换在机器视觉中的深度解析

频率域滤波技术强化

数学原理补充：

• 滤波器通用公式：

  math

  H(u,v) = \frac{1}{1 + [D(u,v)/D_0]^{2n}} \quad \text{(巴特沃斯滤波器)}

  其中 D(u,v) = \sqrt{(u-M/2)^2 + (v-N/2)^2} 为频域点到中心的距离，D₀ 为截止频率，n 控制过渡带陡峭度。

关键细节优化：

1. 振铃效应解决方案：

   • 使用高斯窗函数优化理想滤波器：

     math

     H_{\text{modified}}(u,v) = H_{\text{ideal}}(u,v) \cdot e^{-\frac{D^2}{2\sigma^2}}

   • 巴特沃斯滤波器阶数选择：n=2~4 平衡平滑度与边缘保留

2. 同态滤波参数指南：

   参数	典型值	作用
   γₗ	0.2~0.5	低频压缩强度
   γₕ	1.5~2.5	高频增强强度
   c	0.5~1.0	过渡带斜率

3. 彩色图像处理：

   • 策略1：转换到HSV空间，仅对V(亮度)通道滤波
   • 策略2：在YCbCr空间独立处理Y通道

   python

   # OpenCV 彩色图像频域滤波示例
   img_bgr = cv2.imread("image.jpg")
   img_ycbcr = cv2.cvtColor(img_bgr, cv2.COLOR_BGR2YCrCb)
   Y, Cr, Cb = cv2.split(img_ycbcr)
   Y_filtered = frequency_domain_filter(Y, filter_type="GLPF", D0=30)
   result = cv2.merge([Y_filtered, Cr, Cb])

---

傅里叶描述子技术深化

数学表达与算法：

1. 轮廓参数化：

   • 边界点序列：{(x₀,y₀), (x₁,y₁), ..., (x_{N-1},y_{N-1})}
   • 复数表示：s(k) = x(k) + jy(k), k=0,1,...,N-1

2. 离散傅里叶变换：

   math

   a_n = \frac{1}{N} \sum_{k=0}^{N-1} s(k) e^{-j2\pi nk/N}, \quad n=0,1,...,N-1

   • a₀：中心位置（平移不变性基础）
   • |a₁|：尺度特征
   • ∠aₙ：旋转角度特征

3. 不变性实现：

   python

   # 归一化傅里叶描述子
   descriptors = np.fft.fft(contour_complex)
   descriptors[0] = 0  # 消除平移
   descriptors = descriptors / np.abs(descriptors[1])  # 消除尺度
   descriptors = np.angle(descriptors)  # 消除旋转

应用场景对比：

特征描述子	不变性	计算效率	适用场景
傅里叶描述子	平移+旋转+尺度	高	闭合轮廓物体
SIFT	仿射+光照	中	纹理丰富区域
Hu矩	平移+旋转+尺度	极高	简单形状分类

---

图像配准技术扩展

相位相关法数学推导：

1. 平移定理：

   math

   \mathcal{F}\{f(x-\Delta x, y-\Delta y)\} = F(u,v)e^{-j2\pi(u\Delta x/M + v\Delta y/N)}

2. 互功率谱：

   math

   \frac{F_1(u,v) \cdot F_2^*(u,v)}{|F_1(u,v) \cdot F_2^*(u,v)|} = e^{j2\pi(u\Delta x/M + v\Delta y/N)}

3. 位移提取：

   math

   \delta(x,y) = \mathcal{F}^{-1}\left\{ e^{j2\pi(u\Delta x/M + v\Delta y/N)} \right\}

   峰值位置 (xₚ, yₚ) 即位移量

旋转缩放配准优化流程：

图表

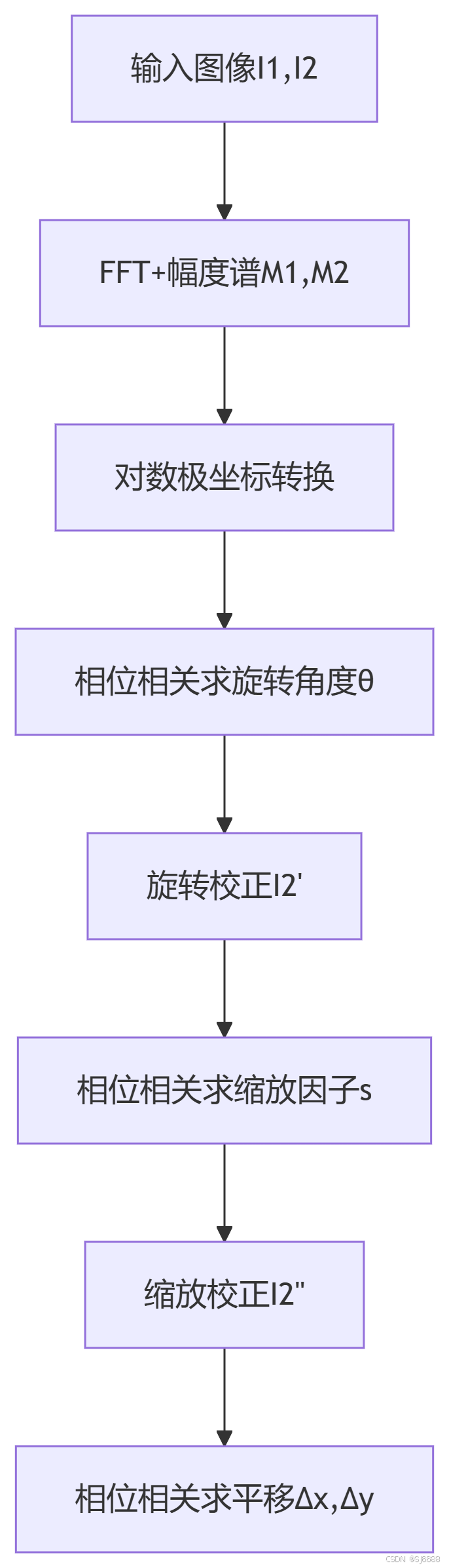
代码

graph TD
A[输入图像I1,I2] --> B[FFT+幅度谱M1,M2]
B --> C[对数极坐标转换]
C --> D[相位相关求旋转角度θ]
D --> E[旋转校正I2']
E --> F[相位相关求缩放因子s]
F --> G[缩放校正I2'']
G --> H[相位相关求平移Δx,Δy]

---

频域卷积的工程实践

复杂度对比分析：

卷积方式	时间复杂度	空间复杂度	适用条件
空间域直接卷积	O(MN·mn)	O(1)	小核(k<15)
频域FFT卷积	O(MN·log(MN))	O(MN)	大核(k>15)
分块重叠相加法	O(MN·log(k))	O(k²)	极大核(k>50)

OpenCV 频域卷积实现：

python

def fft_convolve(img, kernel):
    # 计算填充尺寸
    h, w = img.shape
    kh, kw = kernel.shape
    padded_size = (h + kh - 1, w + kw - 1)
    
    # FFT计算
    img_fft = np.fft.fft2(img, s=padded_size)
    kernel_fft = np.fft.fft2(np.flipud(np.fliplr(kernel)), s=padded_size)
    
    # 频域相乘 + 逆变换
    result = np.fft.ifft2(img_fft * kernel_fft).real
    
    # 裁剪有效区域
    return result[kh//2:kh//2+h, kw//2:kw//2+w]

---

图像重建技术增强

投影切片定理数学表述：

math

\mathcal{F}_1\{p_\theta(t)\} = P_\theta(\omega) = F(\omega \cos\theta, \omega \sin\theta)

其中：

• p_θ(t) 为角度θ的投影
• F(u,v) 为物体2D傅里叶变换

CT重建关键步骤：

1. 正弦图采集：获取0°~180°的投影数据
2. 傅里叶切片：对每个投影进行1D FFT
3. 极坐标插值：将频谱填充到笛卡尔网格
4. 逆FFT重建 ：f(x,y) = \mathcal{F}^{-1}\{F(u,v)\}

重建质量优化技术：

• 滤波反投影(FBP)：使用Ram-Lak滤波器抑制高频噪声

  math

  |\omega| \cdot \text{rect}\left(\frac{\omega}{2\omega_c}\right)

• 迭代重建(SART)：克服投影数据不足问题

---

光学傅里叶变换物理原理

透镜傅里叶变换模型：

图表

代码

graph LR
A[输入平面] --> B[透镜]
B --> C[后焦平面]
C --> D[输出平面]

• 数学描述 ：U_f(u,v) = \frac{e^{jkf}}{j\lambda f} \iint U_o(x,y) e^{-j\frac{2\pi}{\lambda f}(xu+yv)} dxdy
• 4f系统：实现输入-频谱-输出的级联处理

光学相关器实现：

图表

代码

graph LR
S[光源] --> C1[准直镜]
C1 --> SLM1[空间光调制器 输入图像]
SLM1 --> L1[傅里叶透镜]
L1 --> F[匹配滤波器]
F --> L2[傅里叶透镜]
L2 --> CCD[输出相关峰]

优势对比：

特性	光学处理	数字处理
速度	光速(ps级)	受限于CPU/GPU
并行性	天然并行	需特殊硬件
功耗	极低	较高
精度	中等	可达到亚像素级

---

实用建议与最佳实践

1. 频率域滤波参数选择：

   • 截止频率 D₀ = 0.05~0.2 × 图像宽度
   • 巴特沃斯阶数 n=2~4
   • 优先选择高斯滤波器避免振铃效应

2. 傅里叶描述子优化：

   python

   # 抗噪声鲁棒性增强
   k = 15  # 保留低频分量数
   desc = descriptors[:k]  # 保留主要形状信息
   desc /= np.linalg.norm(desc)  # 归一化

3. 频域卷积内存优化：

   python

   # 使用FFTW库提升大图像处理效率
   import pyfftw
   pyfftw.interfaces.cache.enable()
   img_fft = pyfftw.interfaces.numpy_fft.fft2(img, threads=4)

4. CT重建加速技术：

   • GPU并行实现滤波反投影
   • 使用NUFFT(Non-uniform FFT)避免插值误差

---

前沿扩展方向

1. 深度学习融合：

   • Fourier Neural Networks (FNN)：直接在频域进行卷积操作
   • 频域数据增强：在傅里叶空间进行随机滤波

2. 压缩感知应用：

   math

   \min_x \|y - \Phi \Psi x\|_2^2 + \lambda \|x\|_1

   其中 Ψ 为傅里叶变换基

3. 非均匀采样处理：

   • 非均匀傅里叶变换(NUFFT)
   • 径向采样重建技术

4. 量子傅里叶变换：

   • O(N log N) 加速潜力
     免插值误差

---

前沿扩展方向

1. 深度学习融合：

   • Fourier Neural Networks (FNN)：直接在频域进行卷积操作
   • 频域数据增强：在傅里叶空间进行随机滤波

2. 压缩感知应用：

   math

   \min_x \|y - \Phi \Psi x\|_2^2 + \lambda \|x\|_1

   其中 Ψ 为傅里叶变换基

3. 非均匀采样处理：

   • 非均匀傅里叶变换(NUFFT)
   • 径向采样重建技术

4. 量子傅里叶变换：

   • O(N log N) 加速潜力
   • 量子图像处理初步探索