1.排序的概念及运用
1.1概念
排序:就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
1.2运用
现实生活中往往需要通过排序来了解我们所需的事物
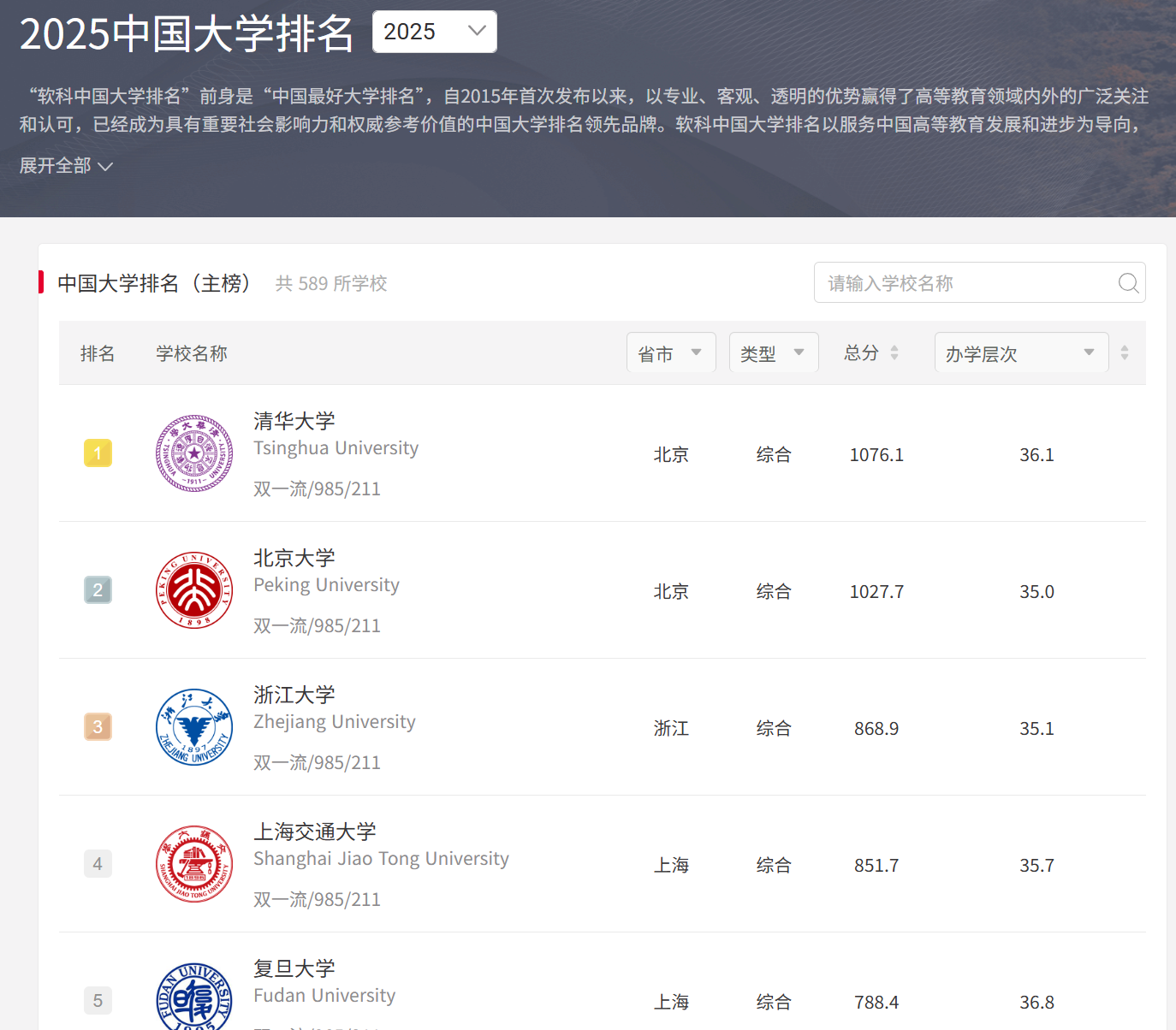
中国大学排名:
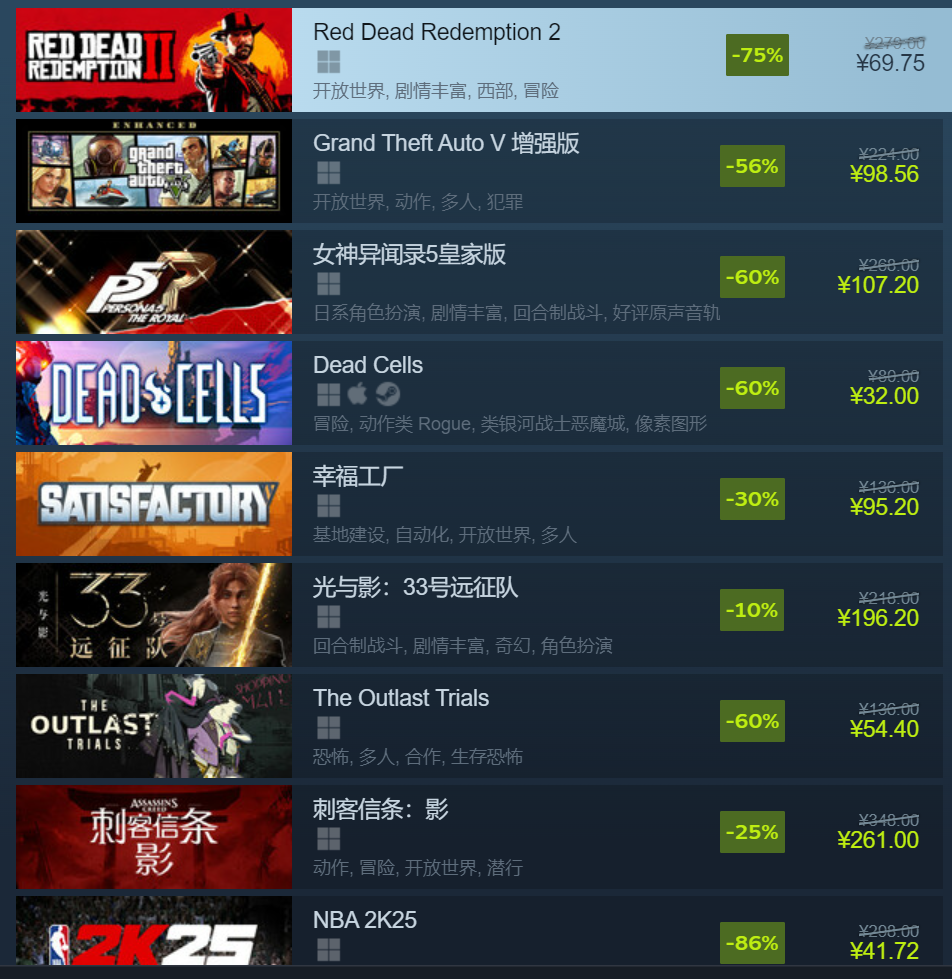
游戏促销排名
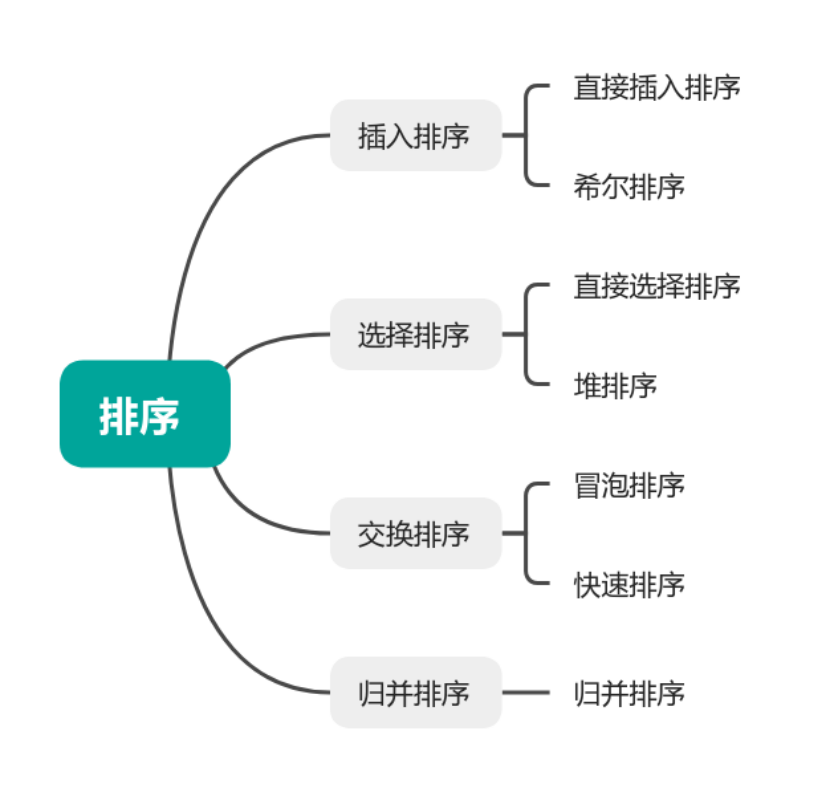
1.3常见的排序算法
排序算法一般分为两大类:
比较排序
非比较排序
2.比较排序算法实现
2.1插入排序
基本思想
直接插入排序是一种简单的插入排序算法,其基本思想是:把待排序的记录按期关键码值的大小逐个插入到一个已经排序好的序列中,直到所有的记录插入完为止,得到一个新的有序序列。
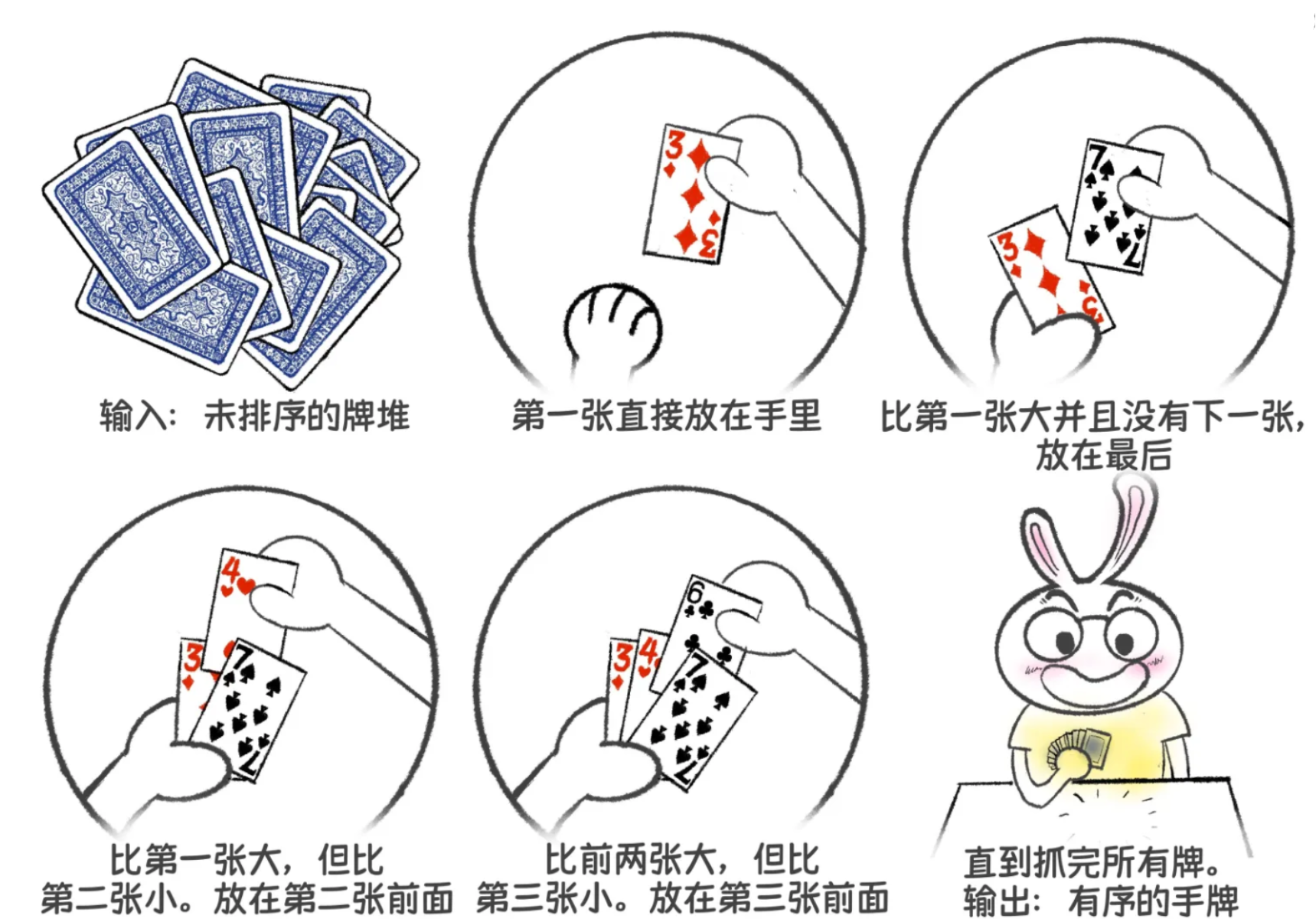
2.1.1直接插入排序

想要把上图翻译成代码,首先要分析:
每一次执行都是将未排序的元素插入到前面,这就需要比较,且要正好找到合适的位置,那么该如何实现这一步?要知道当元素插入到中间时,如"执行的第三轮",我们需要将"3"、"4"都往后挪动一个位置,并将"1"插入到arr[1]的位置。先把待执行的元素用tmp变量暂时存储,同时需要一个"标记",也就是"end",end在每轮执行前都将指向数组最后的位置,而end+1则是其后一个位置,这样当元素后移时,就可以通过"arr[end + 1] = arr[end];"进行实现,通过end--,标记往前移动,直到arr[end]<=tmp,则找到了合适的位置。
cpp
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
end--;
}
else
{
}那么标记不断往前移动的过程也可以看作是一个循环,而循环的条件也就是(1)end>=0 (2) tmp没有找到合适的位置。
cpp
int tmp = arr[end + 1];
while (end>=0)
{
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}若要调整含有6个元素的数组,那么就需要总体循环6次该过程,又是一个循环
最终:
cpp
//直接插入排序
void InserSort(int* arr, int n)
{
for (int i = 0; i < n-1; i++)//注意循环的范围,n-1,确保end+1不会出界
{
int end = i;//end时刻指向已排序数组的最后一位
int tmp = arr[end + 1];
while (end>=0)
{
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}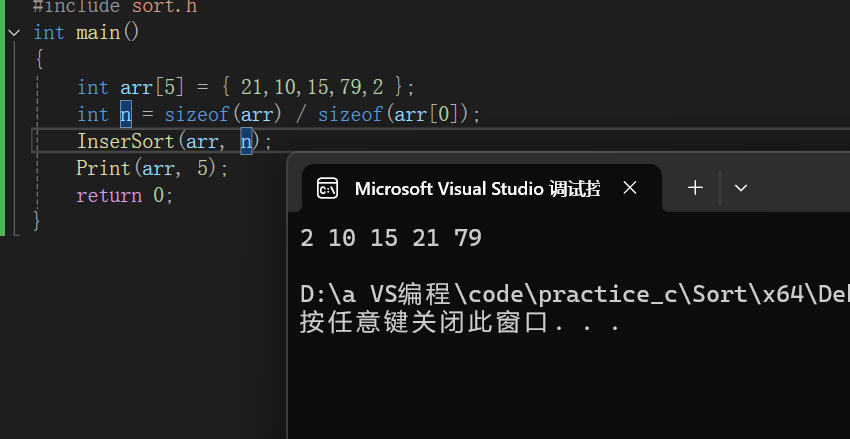
元素越接近有序,直接插入排序算法的时间效率就越高
时间复杂度:0(N^2);
空间复杂度:0(1);
2.1.2希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数(通常是gap=n/3+1),把待排序文件所有记录分成各组,所有的距离相等的记录分在同一组内,并对每一组内的记录进行排序,然后gap=gap/3+1得到下一个整数,再将数组分成各组,进行插入排序,当gap=1时,就相当于直接插入排序。
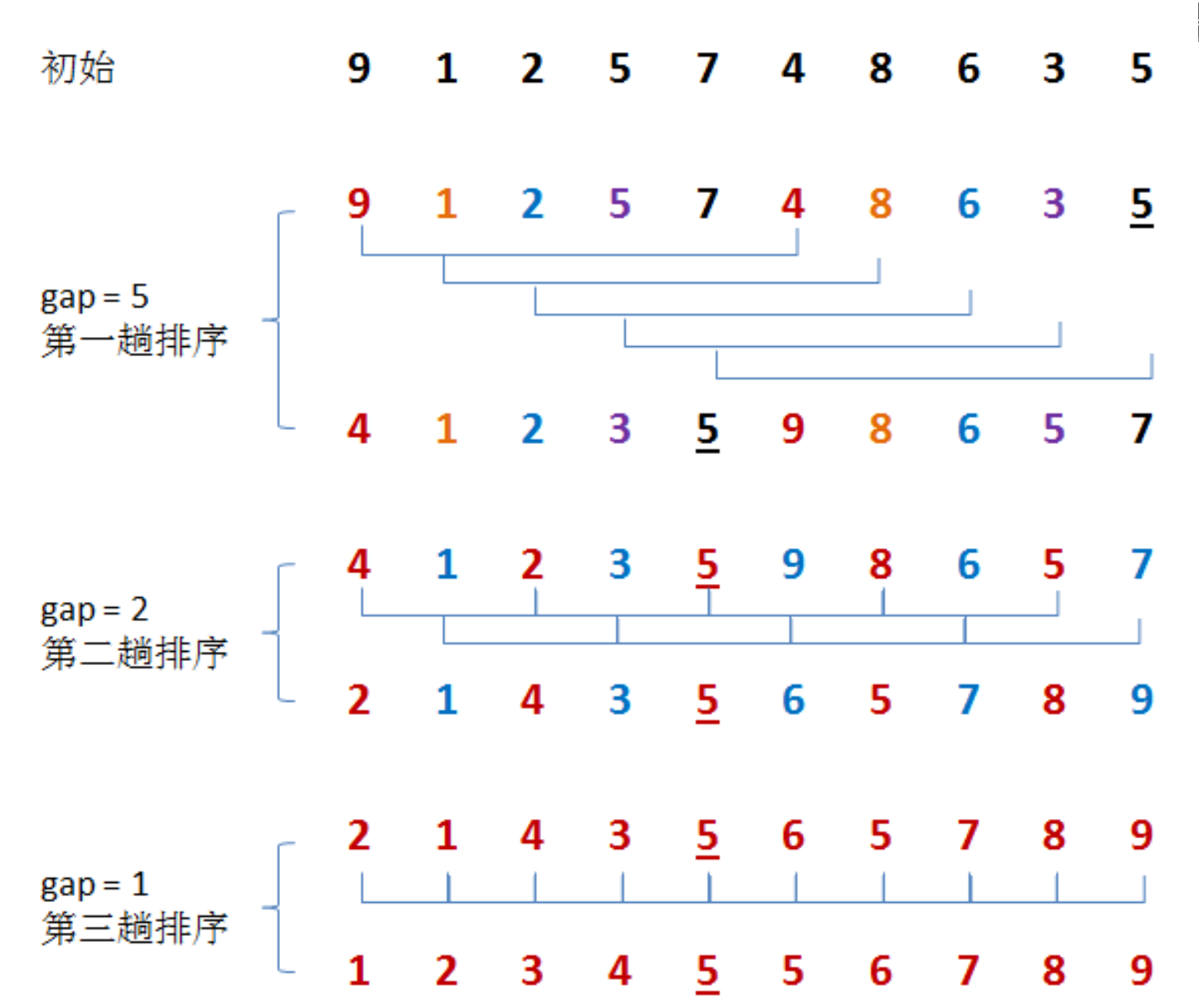
改编直接插入排序,将end+1改为end+gap,同时end每次向前的距离也改为了gap,而一次插入排序算为一组,我们需要通过改变gap的值多次重复执行插入排序。
cpp
//希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while(gap>1)
{
gap = gap / 3 + 1;
//对每组进行插入排序
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end-=gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}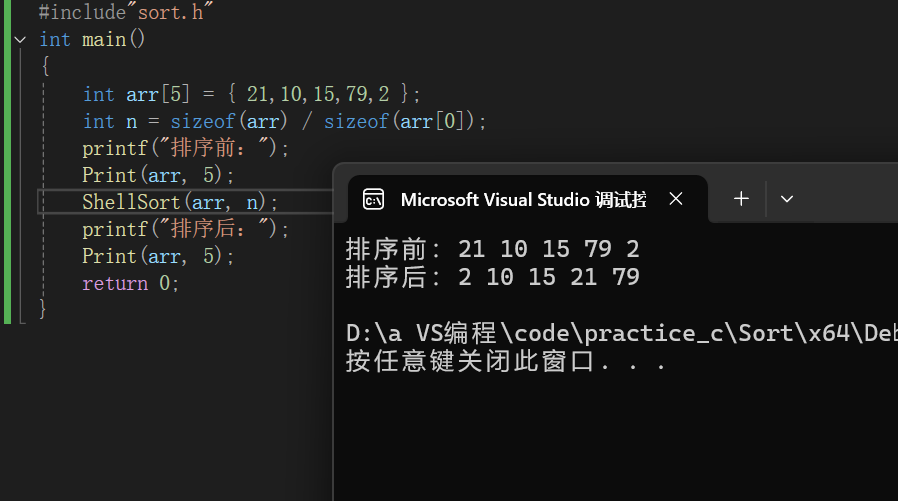
希尔排序时间复杂度不好计算,因为 gap 的取值很多,导致很难去计算,因此很多书中给出的希尔排序的时间复杂度都不固定。
2.2选择排序
选择排序基本思想:
每一次从待排序的数据元素中选出最小的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
2.2.1直接选择排序
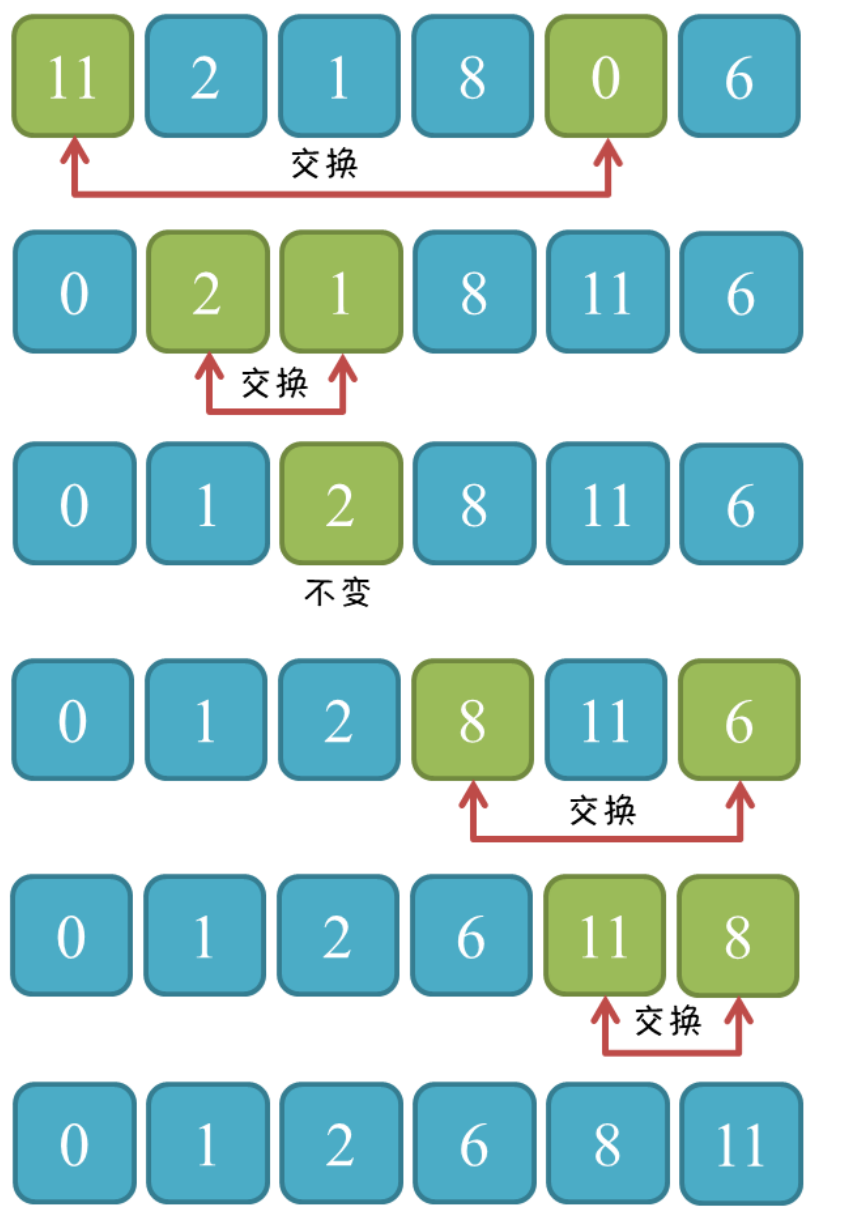

cpp
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
cpp
//直接选择排序
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
//初始化maxi和mini的值
int maxi = begin;
int mini = begin;
for (int i = begin+1; i <=end; i++)
{
//找到mini和maxi
if (arr[i] > arr[maxi])
{
maxi = i;
}
if (arr[i] < arr[mini])
{
mini = i;
}
}
//交换
//mini <-> begin
//maxi <-> begin
if (maxi == begin)//当maxi==begin时,若将arr[mini], arr[begin]后,原最大值的位置跑到了
{ //原mini的位置,为了防止二次交换,需要加一个判断
maxi = mini;
}
Swap(&arr[mini], &arr[begin]);
Swap(&arr[maxi], &arr[end]);
begin++;
end--;
}
}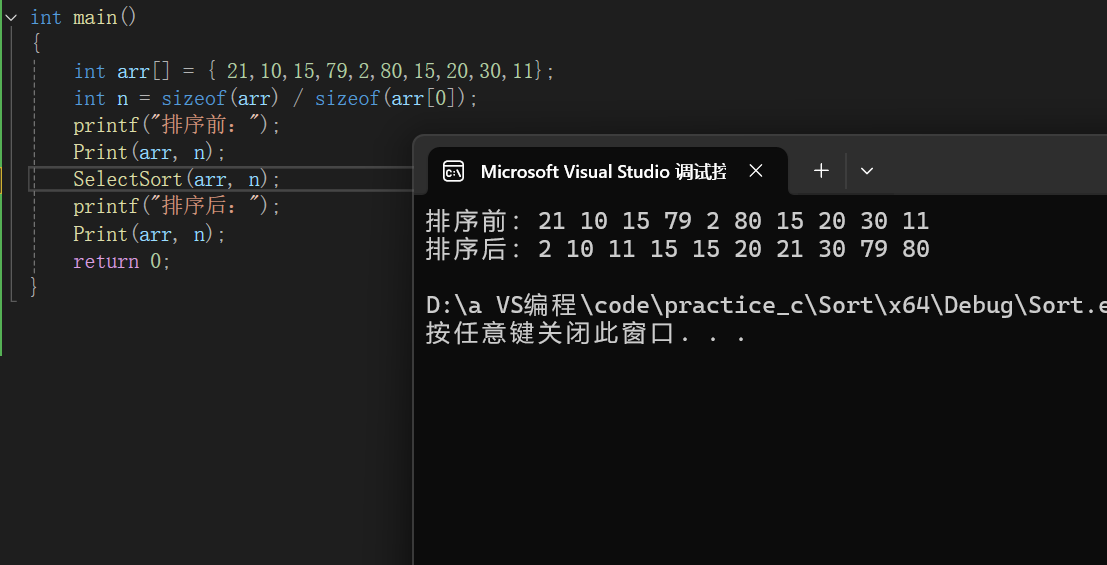
时间复杂度:0(N^2)
2.2.2堆排序
cpp
//向下调整
void AdjustDown(int* arr,int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && arr[child]<arr[child+1])
{
child++;
}
if (arr[child]>arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* arr, int n)
{
for (int i = (n - 2) / 2; i >= 0; i--)
{
AdjustDown(arr, i, n);
}
int end = n - 1;
while (end>0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, 0, end);
end--;
}
}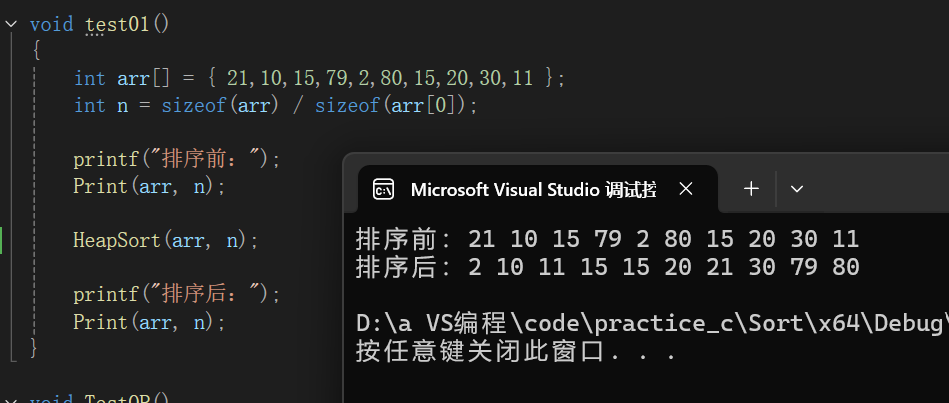
时间复杂度:0(N*logN)
2.3交换排序
交换排序基本思想:
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,
交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动
2.3.1冒泡排序
冒泡排序是一种最基础的交换排序冒泡排序,因为每一个元素都可以像小气泡一样,根据自身大小一点一点向数组的一侧移动。
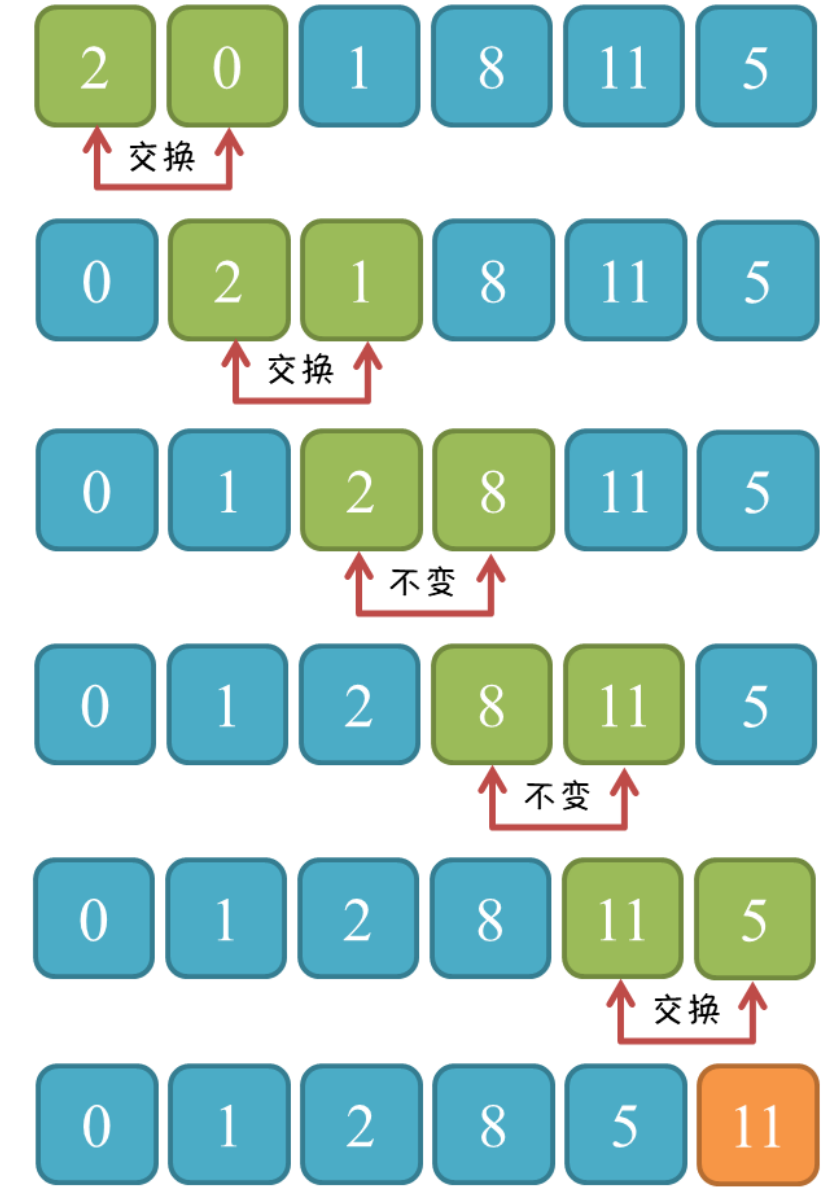

cpp
//冒泡排序
void BubbleSort(int* arr, int n)
{
assert(arr);
for (int i = 0; i < n - 1; i++) {
// 从第 1 个元素开始遍历,遍历至 n-1-i
int flag = 1;
for (int j = 0; j < n - 1 - i; j++) {
//比较 arr[j] 和 arr[j+1] 的大小
if (arr[j] > arr[j + 1]) {
//交换 2 个元素的位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = 0;
}
}
if (flag)//数组内全部有序,提前跳出
{
break;
}
}
}2.3.2快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
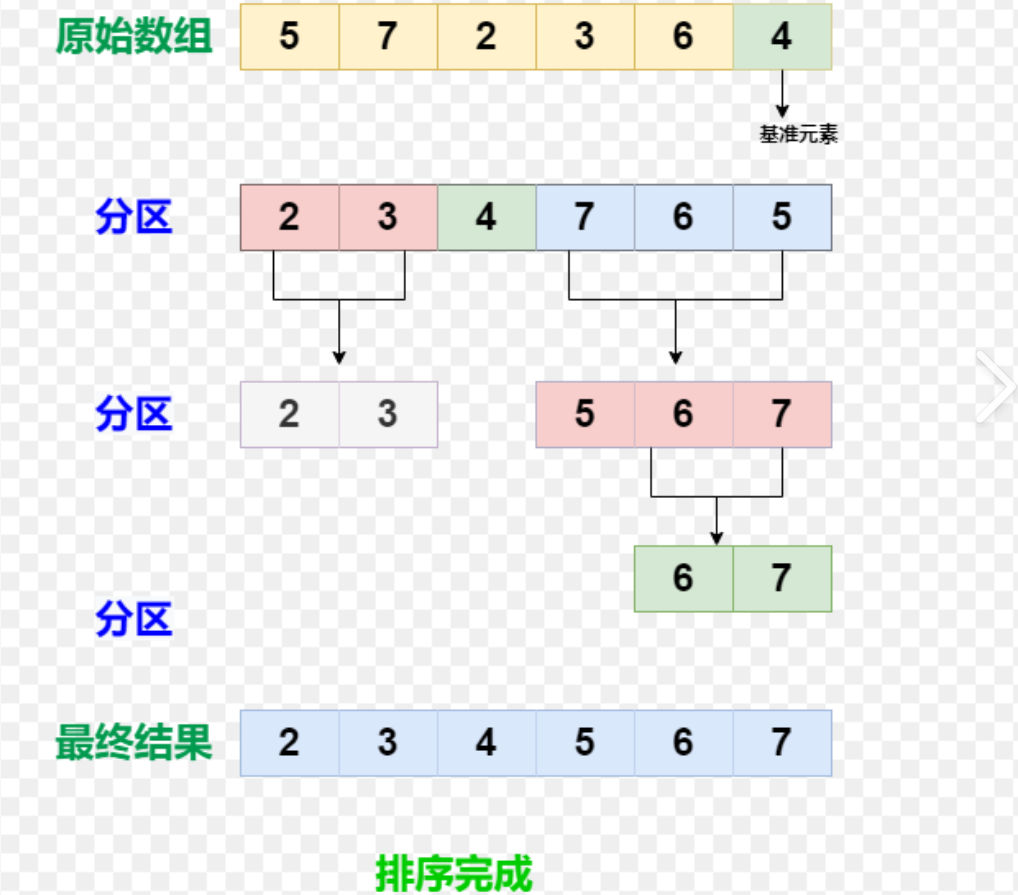
2.3.2.1hoare版本
算法思路:
- 创建左右指针,确定基准值
- 从右向左找出比基准值小的数据,从左向右找出比基准值大的数据,左右指针数据交换,进入下次循环
cpp
int _QuickSort(int*arr,int left,int right)
{
int keyi = left;
++left;
while (left<=right)
{
//right:从右往左 找比基准值更小的
while (left <= right && arr[right] > arr[keyi])
{
right--;
}
//left:从左往右,找比基准值要大的
while(left <= right && arr[left]<arr[keyi])
{
left++;
}
//right left
if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
}
}
Swap(&arr[keyi], &arr[right]);
return right;
}
//快速排序
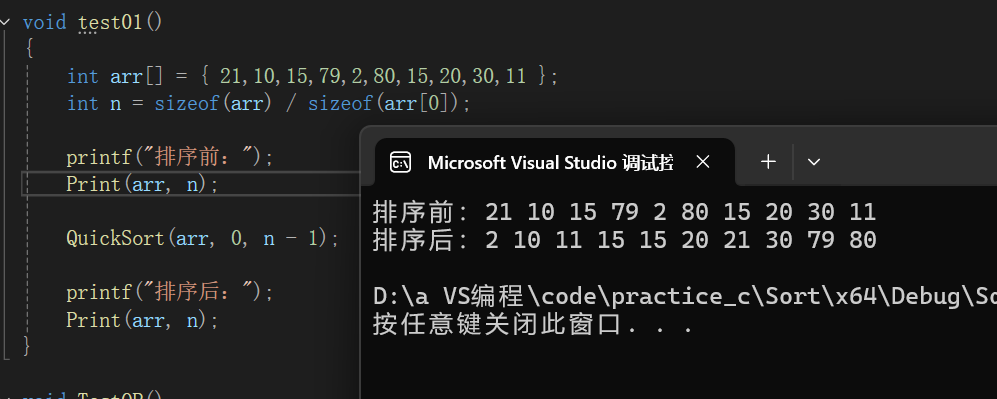
void QuickSort(int* arr, int left, int right)
{
if (left>=right)
{
return;
}
int keyi = _QuickSort(arr,left,right);
//left right
//左序列[left,keyi-1] 右序列[keyi+1,right]
QuickSort(arr, left, keyi - 1);
QuickSort(arr, keyi+1,right);
}
2.3.2.2挖坑法
思路:
创建左右指针。首先从右向左找出比基准小的数据,找到后立即放入左边坑中,当前位置变为新的"坑",然后从左向右找出比基准大的数据,找到后立即放入右边坑中,当前位置变为新的"坑",结束循环后将最开始存储的分界值放入当前的"坑"中,返回当前"坑"下标(即分界值下标)
cpp
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
int hole = left;
int key = a[hole];
while (left < right)
{
while (left<right&&a[right]>key)
{
--right;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] < key)
{
++left;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
if (left>=right)
{
return;
}
int keyi = PartSort2(arr,left,right);
//left right
//左序列[left,keyi-1] 右序列[keyi+1,right]
QuickSort(arr, left, keyi - 1);
QuickSort(arr, keyi+1,right);
}2.3.2.3lomuto前后指针法
创建前后指针,从左到右找比基准值小的进行交换,使得小的都排在基准值的左边。
创建两个变量prev,cur,cur从左往右找比基准值要小的数据,prev和cur交换
cur探路,找比基准值要小的数据
找到了:++prev,prev与基准值交换,cur++
未找到:cur++
cpp
//lomuto前后指针法
int _QuickSort(int*arr,int left,int right)
{
int keyi = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
Swap(&arr[prev], &arr[cur]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
return prev;
}
//快速排序
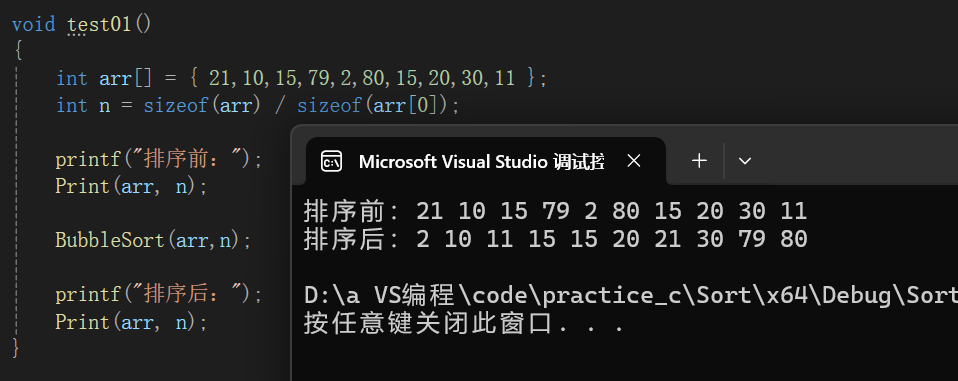
void QuickSort(int* arr, int left, int right)
{
if (left>=right)
{
return;
}
int keyi = _QuickSort(arr,left,right);
//left right
//左序列[left,keyi-1] 右序列[keyi+1,right]
QuickSort(arr, left, keyi - 1);
QuickSort(arr, keyi+1,right);
}
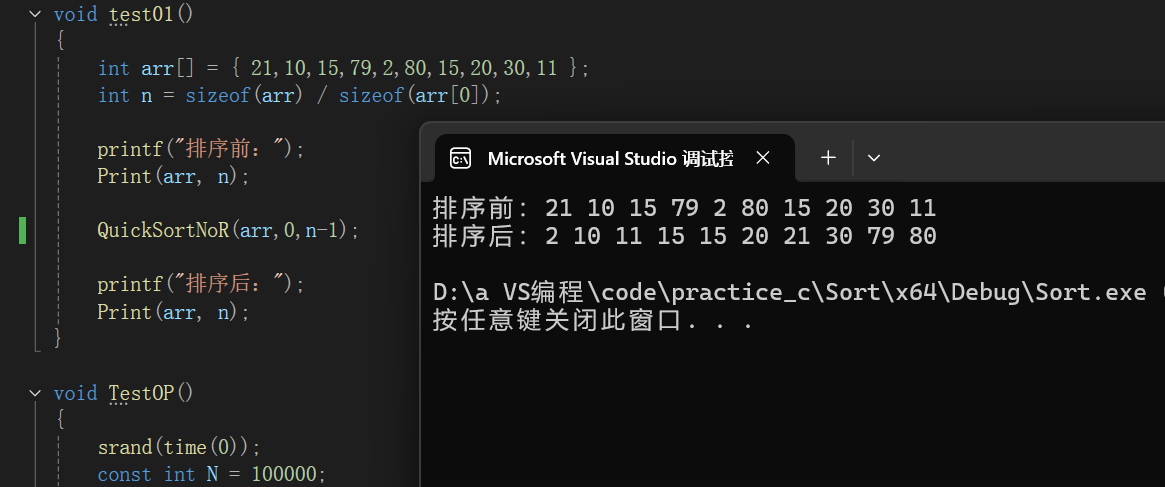
2.3.2.4非递归版本的快速排序
cpp
void QuickSortNoR(int* arr, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
//取栈顶两次
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
//[begin,end]找基准值
int keyi = begin;
int prev = begin, cur = prev + 1;
while (cur<=end)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
Swap(&arr[prev], &arr[cur]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
keyi = prev;
//begin keyi end
//左序列:[begin,keyi-1] 右序列[keyi+1,end];
if (keyi + 1 < end)
{
StackPush(&st, keyi + 1);
StackPush(&st, end);
}
if (begin < keyi - 1)
{
StackPush(&st, begin);
StackPush(&st, keyi - 1);
}
}
StackDestroy(&st);
}
2.4归并排序
归并排序算法思想:
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序核心步骤:
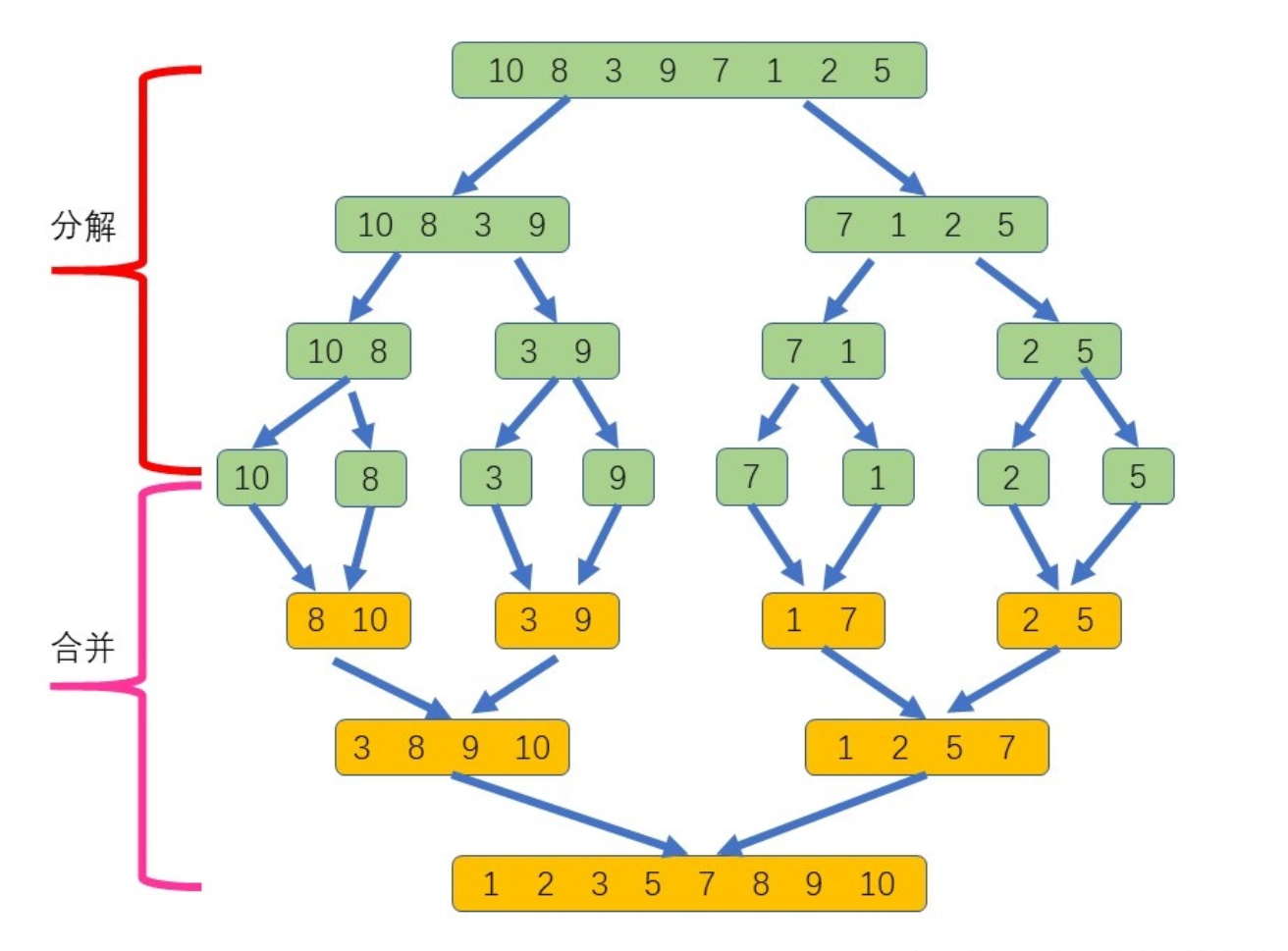
2.4.1归并排序
cpp
//归并排序
void _MergeSort(int* arr, int left,int right,int*tmp)
{
if (left >= right)
{
return;
}
//[left,right]
int mid = (left + right) / 2;
//分左右两个序列[left mid] [mid+1,right]
_MergeSort(arr, left, mid,tmp);
_MergeSort(arr, mid + 1, right,tmp);
//合并两个有序的序列
int begin1 = left, begin2 = mid+1;
int end1 = mid, end2 = right;
//[begin1,end1] [begin2,end2]
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//tmp中有序的数据导入到原数组
//[left,right]
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
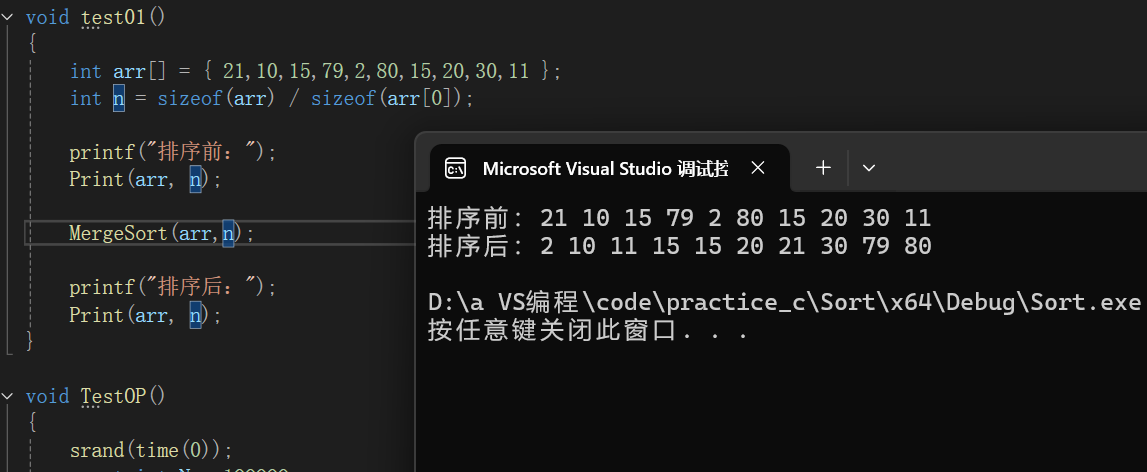
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
时间复杂度:0(n*logn)
2.4.2非递归归并排序,利用
在分解的时候可以发现,数据局部分解,由下到上,每组的数据从1个到2^n个,利用这一特性,创建gap变量,代表每次分组的数据的数量。
cpp
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(1);
}
int gap = 1;
while (gap < n)
{
//根据gap划分组 两两合并
for (int i = 0; i < n; i+=2*gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i+gap, end2 = i +2*gap - 1;
int index = begin1;
//两个有序序列进行合并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1]<a[begin2])
{
tmp[index++] = tmp[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 < end2)
{
tmp[index++] = a[begin2++];
}
//
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
}2.5排序的时间效率大比拼:
通过代码生成10万个随机数据,利用clock函数计算排序的时间(毫秒)
cpp
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
int* a8 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
a8[i] = a1[i];
}
int begin1 = clock();
InserSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
BubbleSort(a5, N);
int end5 = clock();
int begin6 = clock();
QuickSort(a6, 0, N - 1);
int end6 = clock();
int begin7 = clock();
QuickSortNoR(a7, 0, N - 1);
int end7 = clock();
int begin8 = clock();
MergeSort(a1, N);
int end8 = clock();
printf("InserSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("BubbleSort:%d\n", end5 - begin5);
printf("QuickSort:%d\n", end6 - begin6);
printf("QuickSortNoR:%d\n", end7 - begin7);
printf("MergeSort:%d\n", end8 - begin8);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
free(a8);
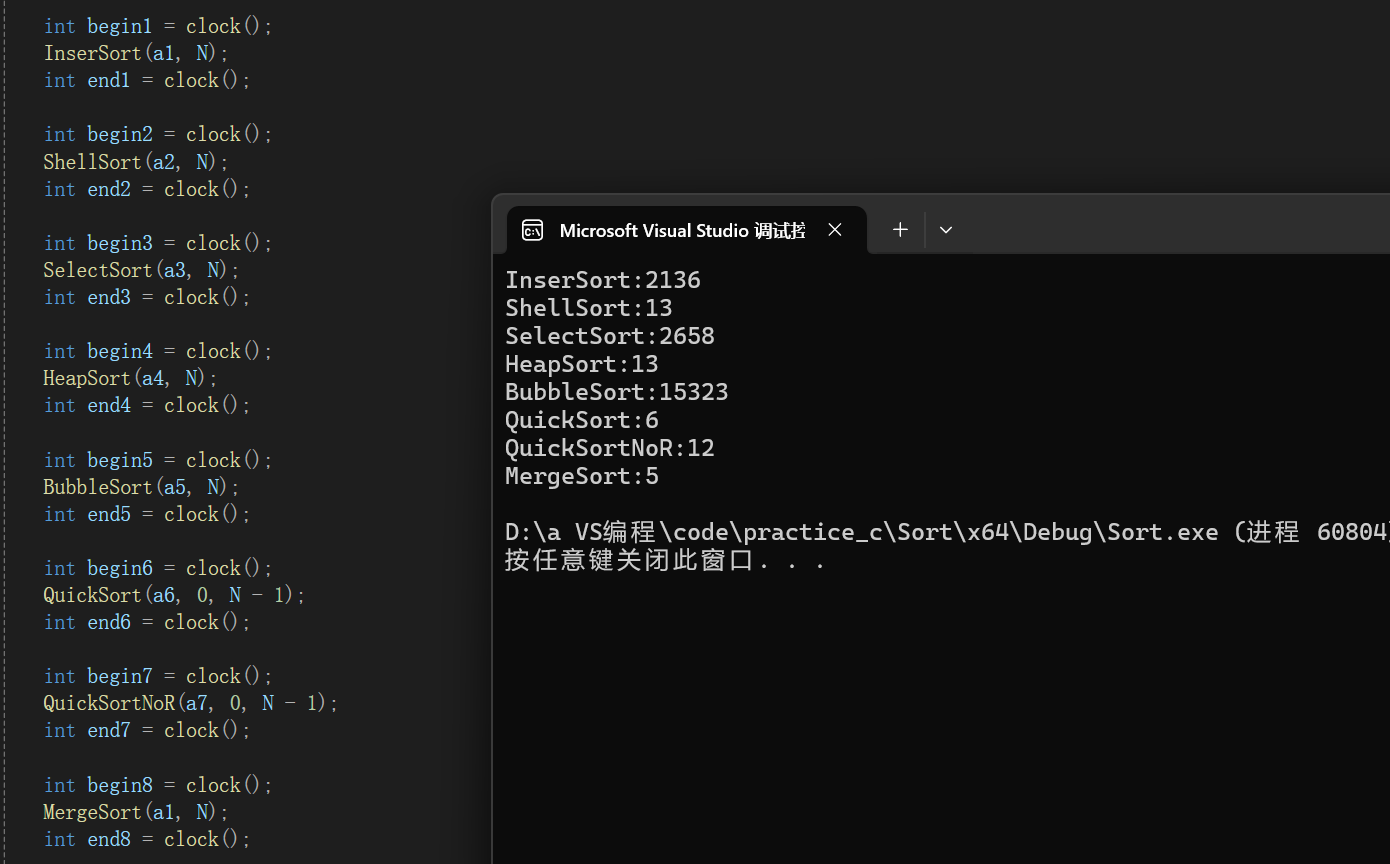
}大比拼结果:
3.非比较排序算法
3.1计数排序
计数排序又称为鸽巢原理,是对哈希直接定址法的变相应用。操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
cpp
//计数排序
void CountSort(int* arr, int n)
{
//找最大和最小值
int min = arr[0], max = arr[0];
for (int i = 0; i < n; i++)
{
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
//max-min确定count数组的大小
int rang = max - min + 1;
int* count = (int*)malloc(sizeof(int) * rang);
if (count==NULL)
{
perror("malloc fail");
exit(1);
}
//
memset(count, 0, sizeof(int) * rang);
for (int i = 0; i < n; i++)
{
count[arr[i] - min]++;
}
//将count数组还原到原数组
int index = 0;
for (int i = 0; i < rang; i++)
{
while (count[i]--)
{
arr[index++] = i + min;
}
}
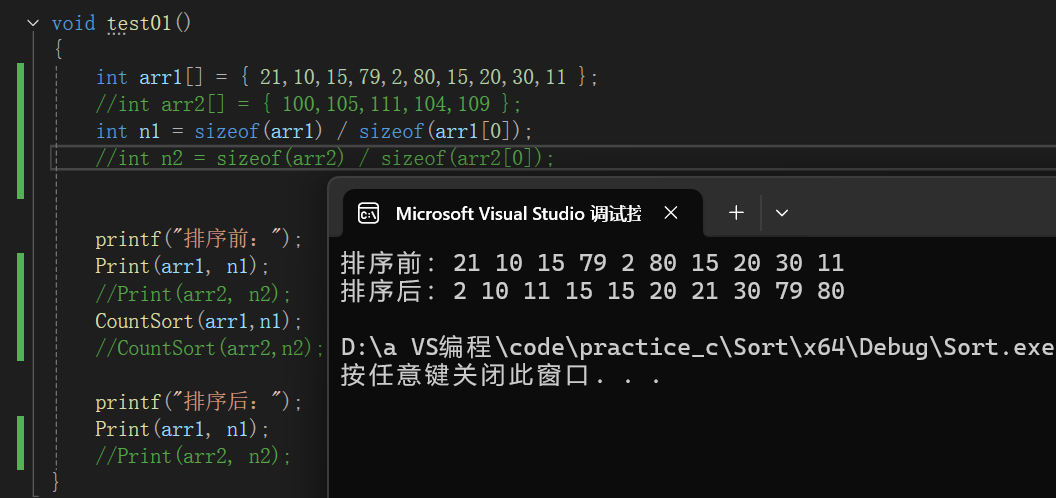
}
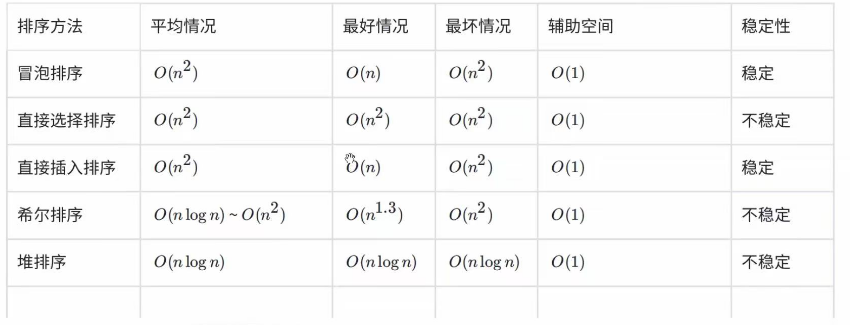
4.排序算法复杂度及稳定性分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r]在r[i]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。