Java数据结构初阶——堆与PriorityQueue

靠沿2025-12-30 12:52

接下来博主会持续更新JavaSE、Java数据结构、MySQL、JavaEE、微服务、Redis等等内容的知识点整理。后续我也会精心制作算法解析、项目经验系列内容，内容绝对干货。相信这些文章能够成为我和大家的"葵花宝典"，喜欢的话就关注一下吧！敬请期待！

文章目录

优先级队列

概念

我们知道队列是一种先进先出(FIFO)的数据结构，但有些情况下， 操作的数据可能带有优先级在这种情况下， 数据结构应该提供两个最基本的操作， 一个是优先返回最高优先级对象， 一个是添加新的对象。

  • 这种数据结构就是优先级队列(Priority Queue)。

优先级队列的模拟实现

JDK1.8中的PriorityQueue底层使用了堆这种数据结构，而堆实际就是在完全二叉树的基础上进行了一些调整。

堆的概念

  • 将一组数据的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，且满足一定的性质。

一下为堆结构的的性质：

  1. 堆中每个节点的值要么不大于其所有子节点的值要么不小于其所有子节点的值节点的值；
  2. 那么将根节点为最大值的堆叫做最大堆或大根堆，根节点为最小值的堆叫做最小堆或小根堆。
  3. 堆的储存顺序一定满足按照一棵完全二叉树的层序遍历的顺序。

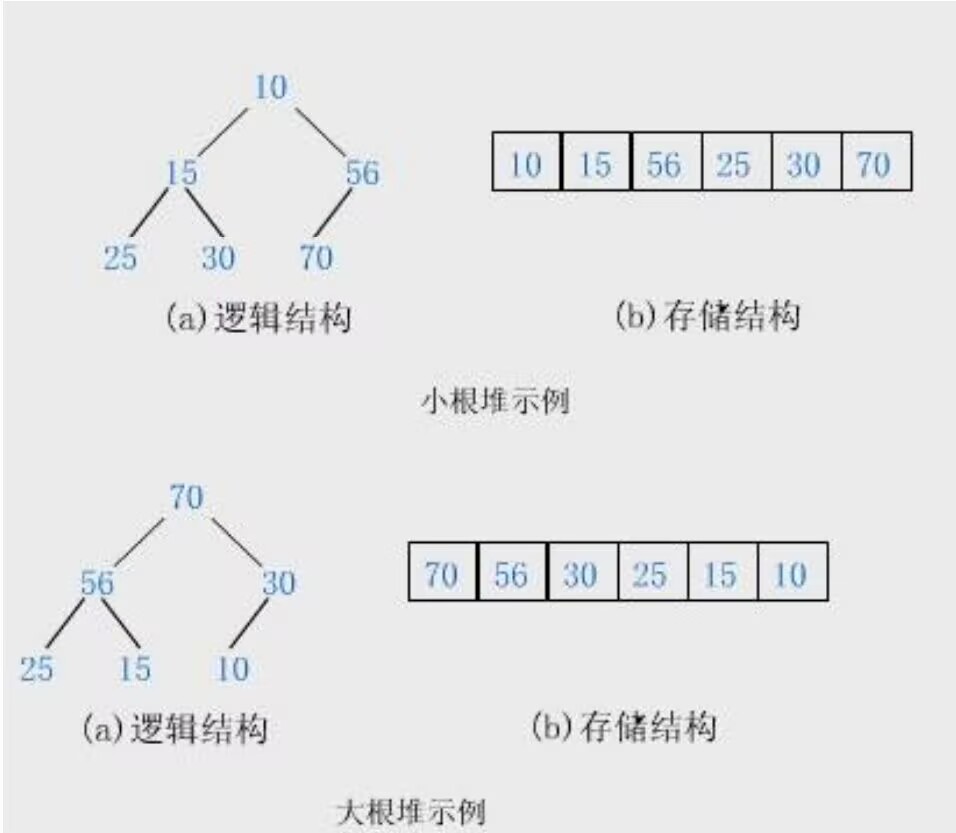
堆的存储方式

  • 从堆的概念可知， 堆是一棵完全二叉树，因此可以使用层序的规则采用顺序的方式来高效存储。

注意：对于非完全二叉树，则不适合使用顺序方式进行存储，因为这种情况下为了能够还原二叉树 ，空间中必须要存储空节点，就会导致空间利用率比较低。

  • 将元素存储到数组中后，假设i为节点在数组中储存时的下标，则有：
    如果i为0，则i表示的节点为根节点。若i不为0，则经计算可得i 节点的双亲节点为（i-1)/2，且节点i的左孩子下标为2*i+1
  • 节点点i的右孩子下标为2*i+2。
  • 要注意计算所得2i+1或2i+2的值（也就是下标）如果>总节点个数减去1，那此时就没有左孩子或右孩子。

将一个普通数组构建为一个堆

java 复制代码 
public class Heap {
    public void creatHeap(int []arr){
        if(arr.length==0) {
            return;
        }
        int child=arr.length-1;
        int parent=(child-1)/2;
        //从下往上遍历堆结构的每个节点，以每一个节点为开始对堆结构进行siftUp(向下调整)
        //这样就可以将一个无序元素集合转化为堆结构
        for(;parent>=0;parent--){
           siftDown(arr,parent);
        }
    }

    public void siftDown(int[] arr,int parent){
        int child=parent*2+1;
        while (child<arr.length){
        		//找出两个子节点中较大的一个
            if(child+1<arr.length&&arr[child]<arr[child+1]){
                child++;
            }
            //如果child比父节点大（优先级高），就将child与父节点调换
            if(arr[child]>arr[parent]){
                swap(arr,child,parent);
                //交换完继续向下检查是否需要继续调整
                parent=child;
                child=parent*2+1;
            }else {
                break;
            }
        }
    }

    private void swap(int[] arr,int i,int j){
        int tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }
}

堆的应用

PriorityQueue的底层实现

PriorityQueue底层是由堆来封装实现的。

那我们自己也可以使用堆来对PriorityQueue模拟实现（深刻理解堆的使用）
注意模拟实现中的offer()、poll()等方法的实现逻辑

java 复制代码 
import java.util.Arrays;

public class PriorityQueue {
    public int[] arr;
    private int usedSize;

    public PriorityQueue() {
        this.arr = new int[20];
    }

    public void offer(int val){
        if(isFull()){
            arr= Arrays.copyOf(arr,arr.length*2);
        }
        //先将val放到堆的最后
        arr[usedSize]=val;
        usedSize++;
        //再以这个元素为起点使用向上调整对堆结构进行重整
        shiftUp(usedSize-1);
    }

    public int poll(){
        if(isEmpty()){
            return -1;
        }
        int ret=arr[0];
        swap(0,usedSize-1);//交换0下标与堆末尾元素的位置
        usedSize--;//删除元素
        shiftDown(0);//由于0下标元素发生变化，则对其进行调整
        return ret;
    }

    public int peek(){
        if(isEmpty()){
            return -1;
        }
        return arr[0];
    }


    public void shiftUp(int child){
        int parent=(child-1)/2;
        while (parent>=0){
            if(arr[child]>arr[parent]){//被offer()调用，这种情况两个子节点之间就不用再比较了，
                swap(child,parent);//因为此堆本来就是大根堆，另一个子节点一定比父节点小。
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

    public void shiftDown(int parent){
        int child=parent*2+1;
        while (child<usedSize){
            if(child+1<usedSize&&arr[child]<arr[child+1]){
                child++;
            }
            if(arr[child]>arr[parent]){
                swap(child,parent);
                parent=child;
                child=parent*2+1;
            }else {
                break;
            }
        }
    }

    private void swap(int i,int j){
        int tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }

    private boolean isFull(){
        return this.usedSize==arr.length;
    }

    private boolean isEmpty(){
        return this.usedSize==0;
    }

}

堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

  1. 建堆
    升序：建大根堆
    降序：建小根堆
  2. 利用堆删除思想来进行排序建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
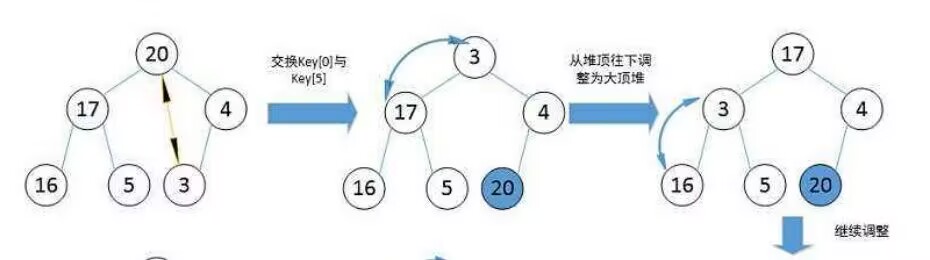
java 复制代码 
//堆排序（从小到大）
public class HeapSort {
    public void heapSort(int[] arr){
        creatHeap(arr);//建大根堆

        int end=arr.length-1;
        //通过循环每次将堆顶元素放到末尾，
        while (end>0) {
            swap(arr, 0, end);
            end--;//堆边界及时调整，避免后续操作再影响到已经排好序的元素
            siftDown(arr,end,0);//每次操作完就立即对因此而变化的堆进行调整（使用siftDown）
        }
    }

//建大根堆
    private void creatHeap(int []arr){
        if(arr.length==0) {
            return;
        }
        int child=arr.length-1;
        int parent=(child-1)/2;
        for(;parent>=0;parent--){
            siftDown(arr,arr.length,parent);
        }
    }

    private void siftDown(int []arr,int end,int parent){
        int child=parent*2+1;
        while (child<end){
            if(child+1<end&&arr[child]<arr[child+1]){
                child++;
            }
            if(arr[child]>arr[parent]){
                swap(arr,child,parent);
                parent=child;
                child=parent*2+1;
            }else {
                break;
            }
        }
    }


    private void swap(int[] arr,int i,int j){
        int tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }
}

常用接口介绍

PriorityQueue的特性

Java集合框架中提供了 PriorityQueue 和 PriorityBlockingQueue 两种类型的优先级

队列，PriorityQueue 是线程不安全的，PriorityBlockingQueue 是线程安全的，这里我们先只介绍一下 PriorityQueue。

PriorityQueue所在的包： java. util. PriorityQueue

关于PriorityQueue的使用要注意：

  1. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出ClassCastException异常。
  2. 不能插入null对象，否则会抛出NullPointerException。

原因：无法比较优先级： PriorityQueue 的核心功能是根据元素的优先级进行排序。而 null 值无法参与有意义的比较操作，毕竟思考一下 null 是应该比非 null 元素具有更高还是更低的优先级？无从得知。如果允许 null 存在，队列的排序机制将无法正常工作。

  1. 根据上面介绍的用堆来模拟实现PriorityQueue的过程可以算出PriorityQueue插入和删除元素的时间复杂度为O(log₂N)，也就是执行次数为二叉树的高度。
  2. PriorityQueue默认情况下是小根堆即每次获取到的元素都是堆中最小的元素。

关于第一条的解释：

  • PriorityQueue 的本质是一个堆数据结构。它出队（ poll ）时总是返回当前队列中优先级最高（即最小或最大）的元素，每次插入操作 ( offer ) 内部都会进行元素的比较和排序。
  • 对于基本包装类：如 Integer , String ，它们本身已经实现了比较规则，可以直接放入。
  • 对于自定义对象：如果你没有提供比较规则， PriorityQueue 在需要比较时（通常是插入第二个元素，因为需要和第一个比较）就会尝试进行类型转换以期找到比较方法，失败后就会抛出 ClassCastException ，提示你这个对象无法被转换为 Comparable 类型。

让对象可比较的核心就是明确告诉Java比较规则，主要有两种方式：

  1. 实现Comparable接口
    这种方式是让元素类自身具备比较能力。需要在定义类时实现 Comparable 接口，并重写 compareTo 方法。具体见博主另一篇文章后半部分：JavaSE知识分享------sort方法，Comparable or Comparator ?

那么当前类实现了Comparable接口之后，再将当前类的对象添加到PriorityQueue 中就合法了。

  • 对于接口中CompareTo方法的返回值，若返回值<0则表示当前对象（ this ）小于参数对象（ o ），而由于PriorityQueue默认是小跟堆，当前对象也就在堆中位置更靠前。
  • 而且在 PriorityQueue 的插入过程中，新插入的对象对应着"当前对象（this）"，而队列中已存在的用于比较的对象是"参数对象（o）"。

2.提供Comparator比较器

java 复制代码 
//创建一个比较器类StudentAgeComparator
//Class ...{
//......
}

具体见博主另一篇文章后半部分：JavaSE知识分享------sort方法，Comparable or Comparator ?

java 复制代码 
// 使用：在构造PriorityQueue时传入这个比较器对象
PriorityQueue<Student> studentQueue = new PriorityQueue<>(new StudentAgeComparator());

Comparator.compare(o1, o2) 方法的返回值规则如下：

  • 若返回负数：表示 o1 在排序顺序上被认为小于 o2 。在默认的小根堆 PriorityQueue 中，这意味着 o1 的优先级比 o2 更高（即更靠近队头）。
  • o1 通常代表新插入的元素。
    o2 通常代表队列中已存在的元素。

那既然PriorityQueue默认是小根堆，应该如何构造一个大根堆呢？

  • 根据上面我们知道PriorityQueue是根据Comparable接口中CompareTo方法返回值，或者是Comparator比较器中的Compare方法返回值来对元素进行优先级排序的。
  • 那么我们只需要颠倒一下对应方法中的返回值就可以完全颠倒元素优先级了，这样也就完成了小根堆到大根堆的转换了。

PriorityQueue常用接口介绍

  1. 优先级队列的构造
java 复制代码 
// 用ArrayList对象来构造一个优先级队列
的对象
ArrayList<Integer> list = new ArrayList
<>();
list. add(4);
list. add(3);
list. add(2);
list. add(1);

PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(list);
  1. 插入/删除/获取优先级最高的元素

Top-k问题

TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素， 一般情况下数据量都比较大。

比如：专业前10名、世界500强、游戏中前100的活跃玩家等。

对于Top-K问题有三种方法可以解决：

  1. 能想到的最简单直接的方式就是对全部数据排序，然后取前k个。但是如果数据量非常大，排序就不太可取了，时间复杂度非常大，甚至可能数据都不能一下子全部加载到内存中。

最佳的方式就是用堆来解决：

  1. 先将数据转换为堆结构储存，使用PriorityQueue.offer()将数据一一储存，前k小元素就要使用小根堆，直接正常offer()。再直接使用PriorityQueue.poll()弹出前k个元素即可。
    而如果是求前k大元素集合就要使用大根堆了，那么这时就需要自定义比较器来处理了。

注意：poll()方法每次执行后会自动使用siftDown（向下调整）来重新将数据调整为堆结构。这样也就使得最终结果就是排好序的TopK数据集合了。

但这样仍不是最优解，下面一种方法是最好的一种解法。

  1. 若求解前k大元素集合，我们可以先任意取k个元素来创建一个小根堆，然后再遍历剩下的元素，每次与堆顶元素（也就堆中最小的元素）比较
  • 若比堆顶元素还要小，就说明此元素不可能在前k大元素当中。
  • 若比堆顶元素大，则说明堆顶元素此时不可能在前k大元素当中了，那么将其poll()，再将此遍历到的元素offer()入队列做为备选项。遍历完成后最终留在队列中的元素就是前k大元素，且堆顶元素还是第k大元素。
    那么如果求解前k小元素集合，我们就对应使用大根堆。就需要定义比较器来处理了。

相关习题：
top-k问题：最小的K个数

上述解法2：

java 复制代码 
import java.util.PriorityQueue;

class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] ret=new int[k];
        if(arr.length==0||k==0){
            return ret;
        }
        PriorityQueue<Integer> que=new PriorityQueue<>();
        int length=arr.length;
        for(int i=0;i<length;i++){
            que.offer(arr[i]);
        }
        for(int i=0;i<k;i++){
            ret[i]=que.poll();
        }

        return ret;
    }
}

上述解法3：

java 复制代码 
class arrComparator implements Comparator<Integer>{
    public int compare(Integer o1,Integer o2){
        return o2-o1;
    }
}


public class Solution2 {
    public int[] smallestK(int[] arr, int k) {
        int[] ret=new int[k];
        if(arr.length==0||k==0){
            return ret;
        }

        PriorityQueue<Integer> que=new PriorityQueue<>(new arrComparator());
        for(int i=0;i<k;i++){
            que.offer(arr[i]);
        }
        int length=arr.length;
        for(int i=k;i<length;i++){
            if(arr[i]<que.peek()){
                que.poll();
                que.offer(arr[i]);
            }
        }
        int i=0;
        while(!que.isEmpty()){
            ret[i]=que.poll();
            i++;
        }

        return ret;
    }
}

觉得文章对你有帮助的话就点个赞，收藏起来这份免费的资料吧！也欢迎大家在评论区讨论技术、经验

相关推荐
先做个垃圾出来………2 小时前
搜索树完整
开发语言·javascript·ecmascript
禾叙_2 小时前
HashMap
java·数据结构·哈希算法
guygg882 小时前
基于MATLAB的64QAM单载波通信系统仿真实现
开发语言·matlab
AI科技星2 小时前
张祥前统一场论电荷定义方程分析报告
开发语言·经验分享·线性代数·算法·数学建模
SadSunset2 小时前
(44)Spring6集成MyBatis3.5(了解即可，大部分用springboot)
java·spring boot·后端
Tan38512 小时前
如何在 OfficeAI 上配置 API Key（图文教程）
开发语言·人工智能·c#·api·教程·officeai
LYOBOYI1232 小时前
qt的事件传播机制
java·前端·qt
PM老周2 小时前
产品路线图怎么做：从愿景到里程碑的 6 步落地法
开发语言·安全·阿里云·团队开发·个人开发
短剑重铸之日2 小时前
《深入解析JVM》第四章：JVM 调优
java·jvm·后端·面试·架构
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03Linux下V2Ray安装配置指南04Claude Code Skills 实用使用手册05电脑检测软件—图吧工具箱06UV安装并设置国内源07jdk21下载、安装（Windows、Linux、macOS）082025-04-03 Latex学习1——本地配置Latex + VScode环境09Web安全中SQL注入绕过WAF的具体手法和实战案例10SQLmap 完整使用指南：环境搭建 + 命令详解 + 实操案例