二叉堆&大根堆&小根堆的介绍和使用

文章目录

• • 一、二叉堆是什么？
  • 二、大根堆是什么
  • 三、小根堆是什么

一、二叉堆是什么？

二叉堆是一种"完全二叉树 + 堆序性质"的数据结构，用来快速获取最大值或最小值。

完全二叉树（结构约束）：

• 树是完全二叉树
• 除了最后一层，其它层必须是满的
• 最后一层 从左往右填

这个性质让它可以用数组存储

堆序性质（值的约束）

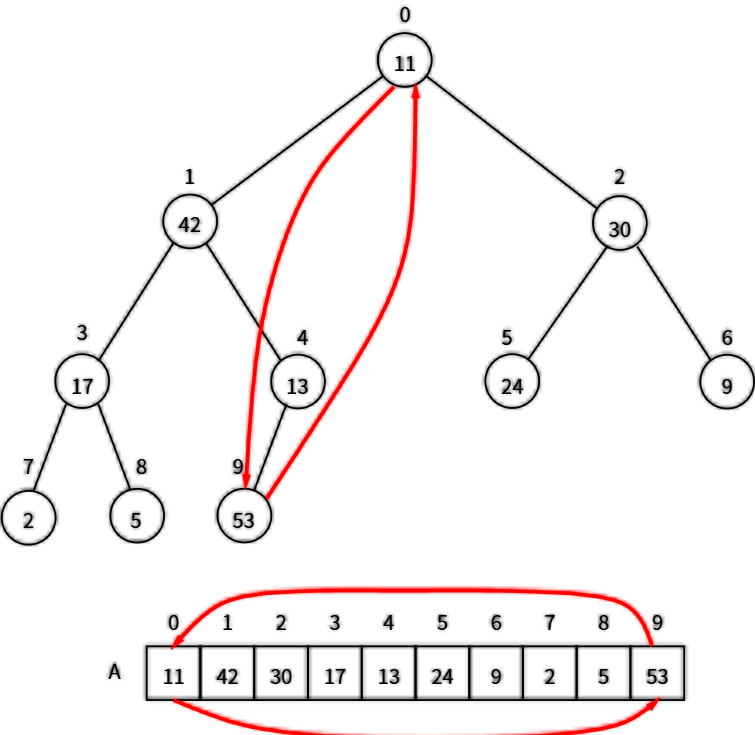
为什么二叉堆可以用数组存？

假设数组下标从 0 开始：

父节点 i
左孩子 = 2*i + 1
右孩子 = 2*i + 2

例子（大顶堆）：

数组: [50, 30, 40, 10, 5, 20]
索引:  0   1   2   3   4   5

            50
          /    \
        30      40
       /  \    /
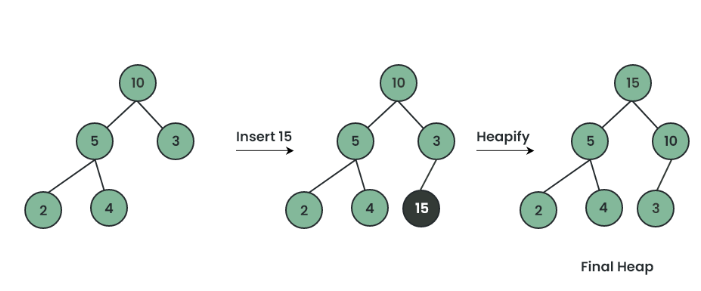
     10    5  20

插入元素（上浮 / sift-up）

步骤：

1. 把新元素放到数组末尾
2. 与父节点比较
3. 如果破坏堆序 → 交换
4. 一直向上，直到合法

删除堆顶（下沉 / sift-down）

步骤：

1. 用最后一个元素覆盖堆顶
2. 删除末尾
3. 与左右孩子中较大（或较小的交换
4. 一直向下，直到合法

二、大根堆是什么

大根堆（Max Heap）是一种完全二叉树，每个父节点的值都 ≥ 它的子节点。堆顶元素永远是"最大值"

大根堆的两个硬性规则

结构规则：完全二叉树

• 除最后一层外，每一层都是满的
• 最后一层从左向右依次填充

数值规则：堆序性质（大根堆）

parent >= left_child
parent >= right_child

大根堆的结构示意（树 ↔ 数组）

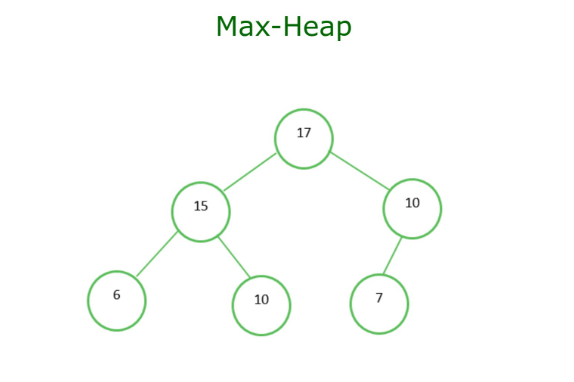
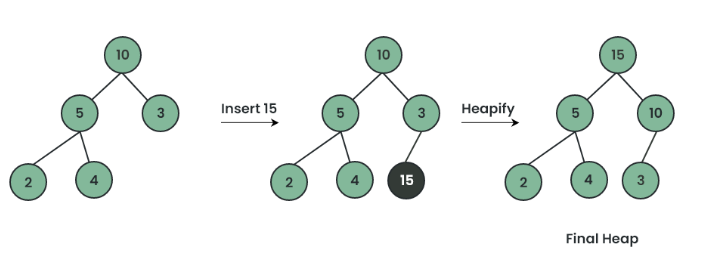
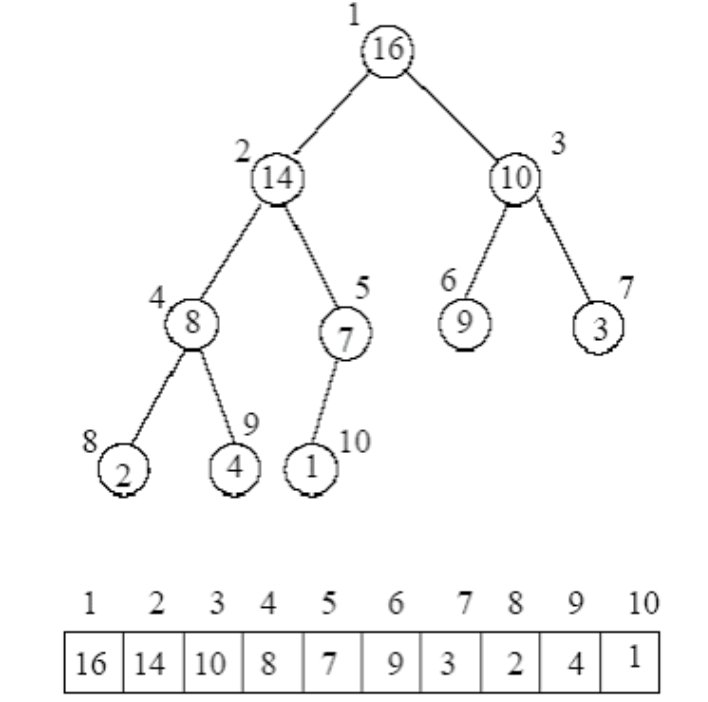
示例大根堆

数组: [90, 70, 60, 40, 30, 20, 10]
索引:  0   1   2   3   4   5   6

              90
           /       \
         70         60
       /   \       /   \
     40    30    20    10

为什么大根堆能用数组实现？

如果下标从 0 开始：

父节点 i
左孩子 = 2*i + 1
右孩子 = 2*i + 2

这正是 完全二叉树的编号规律

插入元素的过程（上浮 / sift-up）
1.插入新元素到堆的末尾

首先，将新元素放入堆的 末尾，即堆的最后一个位置。

假设当前堆的数组表示如下：

堆：[90, 70, 60, 40, 30, 20, 10]
索引：[0, 1, 2, 3, 4, 5, 6]

现在我们要插入新元素 80。步骤如下：

插入前： [90, 70, 60, 40, 30, 20, 10]
插入元素：80

插入后： [90, 70, 60, 40, 30, 20, 10, 80]

2.通过"上浮"（sift-up）恢复堆的性质

接下来，需要 上浮（sift-up）新插入的元素，确保父节点的值始终大于或等于它的子节点的值，从而恢复大根堆的堆序性质。

上浮的具体步骤：

1. 比较新插入元素和它的父节点的值。
2. 如果父节点的值小于新元素的值，就交换它们。
3. 重复此过程，直到新元素不再比其父节点大，或者新元素成为堆顶。

假设当前堆为：

[90, 70, 60, 40, 30, 20, 10]

插入元素：80，新堆为：

[90, 70, 60, 40, 30, 20, 10, 80]

我们从数组末尾（80）开始向上检查，进行上浮：

a.检查 80 和父节点 40（索引 3）：80 > 40，交换 80 和 40，结果如下：

[90, 70, 60, 80, 30, 20, 10, 40]

b.检查 80 和新的父节点 70（索引 1）80 > 70，交换 80 和 70，结果如下：

[90, 80, 60, 70, 30, 20, 10, 40]

c.检查 80 和新的父节点 90（索引 0）80 < 90，不需要交换，插入结束：

最终堆的结果是：

[90, 80, 60, 70, 30, 20, 10, 40]

大根堆删除堆顶元素的过程

1. 将堆顶元素删除，并用堆的最后一个元素 替代堆顶元素。
2. 然后进行 下沉（sift-down） 操作，恢复堆序性质（确保大根堆的性质）。

1.删除堆顶元素，并用最后一个元素替代堆顶

假设我们有一个大根堆：

堆：[90, 70, 60, 40, 30, 20, 10]
索引：[0, 1, 2, 3, 4, 5, 6]

要删除堆顶元素 90，我们将堆的最后一个元素（10）放到堆顶位置：

删除堆顶后：[10, 70, 60, 40, 30, 20]

2.进行下沉（sift-down）操作，恢复堆序

接下来，我们要通过 下沉（sift-down）操作恢复堆的性质。

1. 比较当前节点和左右子节点，选择较大的子节点。
2. 如果当前节点小于较大的子节点，交换它们。
3. 然后将当前节点移到较大子节点的位置，再次进行下沉。
4. 重复此过程，直到当前节点不再小于它的任何子节点，或者它成为叶子节点。

步骤示例

从上面删除堆顶元素后，堆的结构变为：

[10, 70, 60, 40, 30, 20]

我们从新的堆顶开始进行下沉操作，步骤如下：
a.当前节点：10，左右子节点：70 和 60；选择较大的子节点（70），因为 70 > 60，交换 10 和 70，堆变为：

[70, 10, 60, 40, 30, 20]

b.当前节点：10，左右子节点：40 和 30，选择较大的子节点（40），因为 40 > 30；交换 10 和 40，堆变为：

[70, 40, 60, 10, 30, 20]

c.当前节点：10，左右子节点：30 和 20，选择较大的子节点（30），因为 30 > 20；交换 10 和 30，堆变为：

[70, 40, 60, 30, 10, 20]

此时，10 变成了叶子节点，且下沉操作完成。

最终堆的结果是：

[70, 40, 60, 30, 10, 20]

大根堆实现代码：

#include <iostream>
#include <vector>
using namespace std;

class MaxHeap {
private:
    vector<int> heap;

    // 上浮
    void siftUp(int idx)
    {
        while (idx > 0)
        {
            int parent = (idx - 1) / 2;
            if (heap[parent] >= heap[idx]) break;
            swap(heap[parent], heap[idx]);
            idx = parent;
        }
    }

    // 下沉
    void siftDown(int idx)
    {
        int n = heap.size();
        while (true)
        {
            int left = 2 * idx + 1;
            int right = 2 * idx + 2;
            int largest = idx;

            if (left < n && heap[left] > heap[largest])
                largest = left;
            if (right < n && heap[right] > heap[largest])
                largest = right;

            if (largest == idx) break;
            swap(heap[idx], heap[largest]);
            idx = largest;
        }
    }

public:
    void push(int x)
    {
        heap.push_back(x);
        siftUp(heap.size() - 1);
    }

    void pop()
    {
        heap[0] = heap.back();
        heap.pop_back();
        siftDown(0);
    }

    int top() const
    {
        return heap[0];
    }

    bool empty() const
    {
        return heap.empty();
    }
};

三、小根堆是什么

小根堆（Min Heap）是一种完全二叉树数据结构，每个父节点的值都 ≤ 它的子节点，堆顶元素是最小值。

小根堆的特性

结构规则：完全二叉树

• 除了最后一层，其它每一层必须满
• 最后一层的元素从左到右依次填充

数值规则：堆序性质（小根堆）

parent <= left_child
parent <= right_child

小根堆和大根堆的区别

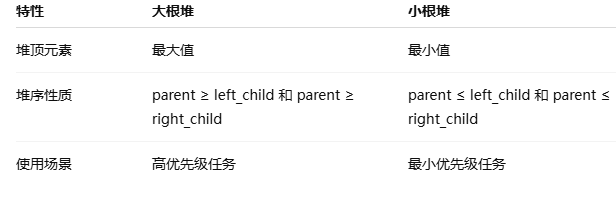
小根堆的结构图示

假设小根堆的数组如下：

数组: [10, 20, 30, 40, 50, 60]
索引:  0   1   2   3   4   5

对应的堆结构：

              10
           /       \
         20         30
       /   \       /
     40     50   60

为什么可以用数组表示小根堆？

1.根节点存储在 数组的第一个位置（索引 0）

2.对于任意索引 i 的节点：

• 左子节点：2*i + 1
• 右子节点：2*i + 2
• 父节点：(i - 1) / 2（整数除法）

这种存储方式节省了指针空间，可以高效地存储和访问。

1.插入元素的过程（上浮 / sift-up）

操作过程：

1. 将新元素插入到堆的末尾。
2. 通过"上浮"（sift-up）操作恢复堆序，确保堆的性质。
3. 重复此过程，直到堆序被恢复。

小根堆插入元素的步骤：
a.将新元素插入堆的末尾

首先，将新元素放入堆的末尾，也就是堆数组的最后一个位置。

假设当前堆的数组表示如下：

堆：[10, 20, 30, 40, 50, 60]
索引：[0, 1, 2, 3, 4, 5]

现在我们要插入新元素 25，步骤如下：

插入前： [10, 20, 30, 40, 50, 60]
插入元素：25

插入后： [10, 20, 30, 40, 50, 60, 25]

b.通过"上浮"（sift-up）恢复堆的性质

接下来，我们需要上浮（sift-up）新插入的元素，确保父节点的值始终小于或等于它的子节点的值，从而恢复小根堆的堆序性质。

上浮的具体步骤：

1. 比较新插入元素和它的父节点的值。
2. 如果父节点的值大于新元素，则交换两者。
3. 重复此过程，直到新元素不再小于其父节点，或者新元素成为堆顶。

步骤示例：

假设当前堆为：

[10, 20, 30, 40, 50, 60]

插入元素：25，新堆为：

[10, 20, 30, 40, 50, 60, 25]

我们从数组末尾（25）开始向上检查，进行上浮：
a.检查 25 和父节点 30（索引 2），25 < 30，交换 25 和 30，结果如下：

[10, 20, 25, 40, 50, 60, 30]

b.检查 25 和新的父节点 20（索引 1），25 > 20，不需要交换，插入结束：

[10, 20, 25, 40, 50, 60, 30]

最终堆的结果是：

[10, 20, 25, 40, 50, 60, 30]

2.删除堆顶元素的过程（下沉 / sift-down）

操作过程：

1. 将堆顶元素删除，并用 堆的最后一个元素 替代堆顶元素。
2. 然后执行"下沉"（sift-down）操作：与左右子节点比较，选择较小的一个与当前节点交换，直到堆序恢复。

小根堆删除堆顶元素的步骤：
a.删除堆顶元素，并用最后一个元素替代堆顶

首先，删除堆顶元素并用堆的最后一个元素 替代堆顶位置。然后删除数组末尾的元素。

假设当前小根堆为：

堆：[10, 20, 30, 40, 50, 60]
索引：[0, 1, 2, 3, 4, 5]

我们要删除堆顶元素 10，将堆的最后一个元素（60）替代堆顶：

删除堆顶后：[60, 20, 30, 40, 50]

b.进行下沉（sift-down）操作，恢复堆的性质

接下来，我们需要下沉（sift-down）操作来恢复堆的性质，确保堆序性质（每个父节点的值小于等于其子节点的值）。

下沉的具体步骤：

1. 比较当前节点与其左右子节点的值，选择较小的子节点。
2. 如果当前节点大于较小的子节点，则交换它们。
3. 将当前节点移动到较小的子节点位置，然后重复上述步骤，直到堆序恢复。

步骤示例：

假设当前堆为：

堆：[60, 20, 30, 40, 50]
索引：[0, 1, 2, 3, 4]

删除堆顶元素：我们首先删除堆顶元素60，然后将堆的最后一个元素（50）放到堆顶的位置，得到：

删除堆顶后：[50, 20, 30, 40]

接下来，进行下沉操作：
a.当前节点：50，左右子节点：20 和 30，选择较小的子节点 20，因为 20 < 30；交换 50 和 20，堆变为：

[20, 50, 30, 40]

b.当前节点：50，左右子节点：40 和 60。选择较小的子节点 40，因为 40 < 60。交换 50 和 40，堆变为：

[20, 40, 30, 50]

c.当前节点：50，左右子节点：无；50 已经没有子节点，且下沉完成。

最终堆的结果是：

[20, 40, 30, 50]

小根堆实现代码：

#include <iostream>
#include <vector>
using namespace std;

class MinHeap {
private:
    vector<int> heap;

    // 上浮
    void siftUp(int idx) {
        while (idx > 0) {
            int parent = (idx - 1) / 2;
            if (heap[parent] <= heap[idx]) break;
            swap(heap[parent], heap[idx]);
            idx = parent;
        }
    }

    // 下沉
    void siftDown(int idx) {
        int n = heap.size();
        while (true) {
            int left = 2 * idx + 1;
            int right = 2 * idx + 2;
            int smallest = idx;

            if (left < n && heap[left] < heap[smallest]) smallest = left;
            if (right < n && heap[right] < heap[smallest]) smallest = right;

            if (smallest == idx) break;
            swap(heap[idx], heap[smallest]);
            idx = smallest;
        }
    }

public:
    // 插入
    void push(int x) {
        heap.push_back(x);
        siftUp(heap.size() - 1);
    }

    // 删除堆顶
    void pop() {
        heap[0] = heap.back();
        heap.pop_back();
        siftDown(0);
    }

    // 获取堆顶元素
    int top() const {
        return heap[0];
    }

    bool empty() const {
        return heap.empty();
    }
};