图论：Dijkstra算法

昨天介绍了最小生成树的两个算法，最小生成树的两个算法旨在求解无向有权图中的最小代价联通图的问题，那么对于有向有权图，从起点到终点的最小花费代价问题就可以用 Dijkstra 算法来解决而且Dijkstra算法可以求出来从起始点开始到所有节点的最短距离！他和最小生成树的prim算法十分类似，也是三部曲，最短路是图论中的经典问题即：给出一个有向图，一个起点，一个终点，问起点到终点的最短路径。

朴素版Dijkstra算法

dijkstra算法：在有权图（权值非负数）中求从起点到其他节点的最短路径算法。

dijkstra 算法可以同时求起点到所有节点的最短路径

权值不能为负数

dijkstra三部曲：

第一步，选源点到哪个节点近且该节点未被访问过
第二步，该最近节点被标记访问过
第三步，更新非访问节点到源点的距离（即更新ans数组）

ans数组用来记录每一个节点距离起始点的最小距离。

循环n次，每一次都能确定一个最优点（其实和prim算法一样都是用了贪心的策略，因为之后的所有的点的选取都是基于目前所有的可达路径，所以要在当前所有的可达路径中选一个权值最小的路径，以其为基准再继续更新之后的可达点，当一个点被更新到最短路中的时候【即被标记访已访问的时候】，就说明在他之前所有可以到达他的路径都遍历过了，因为他是被所有的前面的可达他的点都遍历过的）。

说多了容易迷糊，来看一个模版题来促进对算法以及代码模板的理解

参加科学大会

题目链接：参加科学大会

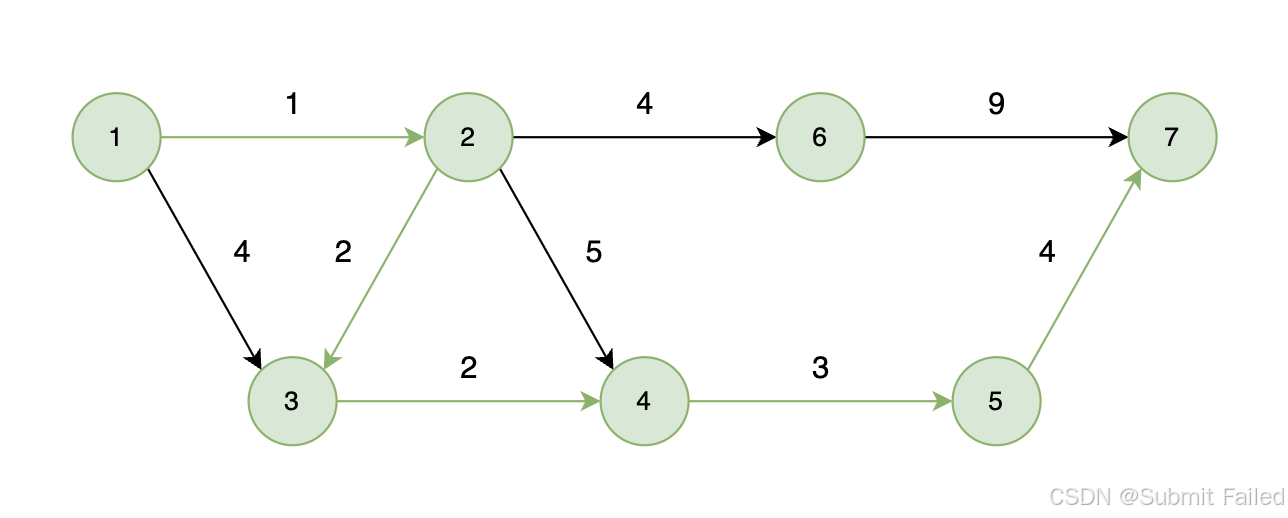
这道题还是相对简单一点的，因为已经固定了起点是1，终点是n，所以不需要对起点和终点进行分析，直接套用模板即可。注意建图的时候如果用邻接矩阵时开[n][n]二维数组m只是边数！

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;
int n,m;

void solve()
{
	cin>>n>>m;
	vector<vector<int>> e(n+1,vector<int>(n+1,inf));//建图
    vector<bool> v(n+1,false);//标记数组
    vector<int> ans(n+1,inf);//所有的点到起点的最短距离（最小代价）
    for(int i=1;i<=m;i++)
    {
        int u,v,w;cin>>u>>v>>w;
        e[u][v] = w;//建图
    }
    ans[1] = 0;
    //Dijkstra算法三部曲
    for(int i=1;i<=n;i++)
    {
        int mi = inf;
        int index = 0;
        //遍历找不在未访问的距离起点最近的点
        for(int j=1;j<=n;j++)//因为之后的所有答案都会在现在的路径基础上累加 所以在现有路径中挑最短的
        {
            if(!v[j] && ans[j] < mi)
            {
                mi = ans[j];
                index = j;
            }
        }
        //将最近点标记为已访问
        v[index] = true;
        //更新所有未访问的可达点到起点的最短距离
        for(int j=1;j<=n;j++)
        {
            if(!v[j] && e[index][j] + ans[index] < ans[j]) ans[j] = ans[index] + e[index][j];
        }
    }
    if(ans[n] == inf) cout<<"-1"<<endl;
    else cout<<ans[n]<<endl;
}

signed main()// Don't forget pre_handle!
{
	IOS
	int T=1;
//	cin>>T;
	while(T--) solve(); 
	return 0;
}

这里奉上Dijkstra朴素版的模板，ICPCer可拿~【适用于n<=1e3且没有负边权（用SPFA）】

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;  // 定义无穷大

void solve()
{
    // 输入点数和边数
    int n,m;
    cin>>n>>m;
    // 邻接矩阵存图，初始化为inf
    vector<vector<int>> e(n+1,vector<int>(n+1,inf));
    // 标记数组，记录是否已确定最短路
    vector<bool> v(n+1,false);
    // 存储起点到各点的最短距离
    vector<int> ans(n+1,inf);
    // 建图，处理边输入
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        e[u][v]=w;  // 有向图建边
        // e[v][u]=w; // 如果是无向图需要加上这行
    }
    // 初始化，起点距离设为0
    ans[1]=0;//起点和终点看题目要求
    // Dijkstra主过程，循环n次
    for(int i=1;i<=n;i++)
    {
        int mi=inf;     // 当前未处理节点中的最小距离
        int index=0;    // 对应的节点编号
        
        // 遍历所有节点，找出未处理且距离最小的节点
        for(int j=1;j<=n;j++)
        {
            if(!v[j]&&ans[j]<mi)
            {
                mi=ans[j];
                index=j;
            }
        }
        // 标记该节点已处理
        v[index]=true;
        
        // 松弛操作：通过该节点更新其他节点的距离
        for(int j=1;j<=n;j++)
        {
            if(!v[j]&&e[index][j]+ans[index]<ans[j])
            {
                ans[j]=ans[index]+e[index][j];
            }
        }
    }
    // 输出结果，如果不可达输出-1
    if(ans[n]==inf) cout<<"-1"<<endl;
    else cout<<ans[n]<<endl;
}
signed main()
{
    IOS;
    int T=1;
    //cin>>T;
    while(T--)
    {
        solve();
    }
    return 0;
}

堆优化版Dijkstra

题目重现

堆优化就是利用小顶堆来避免每次都遍历寻找最值，并且用邻接表代替邻接矩阵更能优化第二个for循环，因为邻接表中存的就是这个点之后所连接的点，直接用auto遍历即可，不过需要分清里面的fi和se分别都对应的哪些变量！

参加科学大会：堆优化版代码：

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 520;
vector<vector<pii>> e(N);//邻接表
vector<int> ans(N,inf);//各个点到起点的最近距离
vector<bool> f(N,false);//标记访问数组
priority_queue<pii,vector<pii>,greater<pii>> q;//最小堆优化
int n,m;

void solve()
{
	cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;cin>>u>>v>>w;
        e[u].push_back({v,w});//用邻接表建图
    }
    ans[1] = 0;
    q.push({ans[1],1});//fi为ans se为索引
    while(!q.empty())
    {
        int mi = q.top().fi;
        int index = q.top().se;
        q.pop();
        if(f[index]) continue;//如果访问过就continue！！！！！
        f[index] = true;
        for(auto i : e[index])
        {
        	//i.fi是点的索引 i.se是边权
            if(ans[index] + i.se < ans[i.fi])
            {
                ans[i.fi] = ans[index] + i.se;
                q.push({ans[i.fi],i.fi});//别忘记在找到一个点之后就更新ans[i.fi]
                //在找到更优解的时候再加入队列!!!
            }
        }
    }
    if(ans[n] == inf) cout<<"-1"<<endl;
    else cout<<ans[n]<<endl;
}

signed main()// Don't forget pre_handle!
{
	IOS
	int T=1;
//	cin>>T;
	while(T--) solve(); 
	return 0;
}

这里同样奉上堆优化版的模板，ICPCer可拿~

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 520;

// Dijkstra堆优化模板（邻接表实现）
// 适用情况：稀疏图，点数较多（mlogn复杂度）
// 功能：求单源最短路，解决非负权图
// 注意：inf需要根据题目调整，避免溢出

vector<vector<pii>> e(N);  // 邻接表存图
vector<int> ans(N, inf);   // 存储起点到各点的最短距离
vector<bool> f(N, false);  // 标记是否已确定最短路
priority_queue<pii, vector<pii>, greater<pii>> q;  // 小根堆优化
int n, m;

void solve()
{
    cin >> n >> m;
    // 邻接表建图
    for(int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        e[u].push_back({v, w});  // 有向图建边
        // e[v].push_back({u, w}); // 无向图需要加上这行
    }
    // 初始化起点距离
    ans[1] = 0;
    q.push({ans[1], 1});  // first存距离，second存节点编号
    // Dijkstra主过程
    while(!q.empty())
    {
        int mi = q.top().fi;    // 当前最小距离
        int index = q.top().se; // 对应节点
        q.pop();
        
        // 如果该节点已确定最短距离，跳过
        if(f[index]) continue;
        f[index] = true;  // 标记已确定
        // 遍历所有邻接点
        for(auto i : e[index])
        {
            // i.fi是邻接点索引，i.se是边权
            if(ans[index] + i.se < ans[i.fi])
            {
                ans[i.fi] = ans[index] + i.se;  // 松弛操作
                q.push({ans[i.fi], i.fi});      // 将新距离加入堆
            }
        }
    }
    // 输出结果
    if(ans[n] == inf) cout << "-1" << endl;
    else cout << ans[n] << endl;
}

signed main()
{
    IOS;
    int T = 1;
    //cin >> T;
    while(T--)
    {
        solve();
    }
    return 0;
}

一定一定要注意访问过就continue!每次的操作（步骤1和3都是对未访问元素的操作!）

接下来就运用一下Dijkstra算法吧！

代价转移

题目链接：代价转移

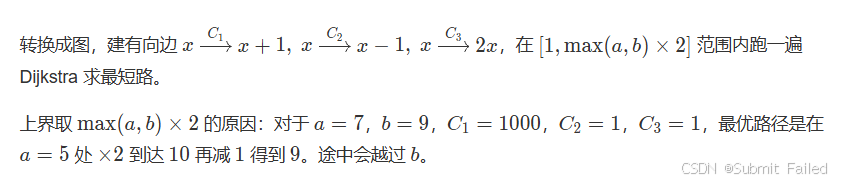
这道题与众不同的就是没有直接给出图的构造，而是需要不断的动态的更新，不过换汤不换药，不过要注意对于动态生成的节点要判断是否合理，如果不合理的话就应该continue防止导致未定义越界（负节点或超大节点）导致死循环！max(a,b) * 2仅仅是合理的范围，不是动态生成的点的范围

下面来看详细代码：

cpp 复制代码

// Problem: 代价转移
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/113664/B
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;

void solve()
{
	int a,b,c1,c2,c3;
	cin>>a>>b>>c1>>c2>>c3;
	if(a >= b)//对特殊情况进行判断
	{
		cout<<(a - b) * c2 <<endl;
		return ;
	}
	//Dijkstra求最短路:
	int N = max(a,b) * 2;//先预定一个可达点范围
	vector<int> ans(N+1,inf);//初始化为最大
	vector<bool> v(N+1,false);//标记访问数组
	priority_queue<pii,vector<pii>,greater<pii>> q;//小顶堆
	ans[a] = 0;//依旧初始化
	q.push({0,a});//首先将起点入队
	while(!q.empty())
	{
		int value = q.top().fi;//直接找出最小值
		int index = q.top().se;//q.fi是代价 q.se数
		q.pop();//将这个点放入最短路径中了（不在非访问的数里面了）
		if(v[index]) continue;//一定一定别忘记 Dijkstra的核心
		v[index] = true;//标记已访问
		pii adj[] = {{index + 1,c1},{index - 1,c2},{index * 2,c3}};//动态生成三个新节点
		for(auto i : adj)//对三个节点进行遍历
		{
			if(i.fi < 1 || i.fi > N) continue;//注意要对新节点的合理性检查 常规图中都是合理点 但是这里是不断动态生成的点 需要检查
			if(ans[index] + i.se < ans[i.fi])//更新更优解
			{
				ans[i.fi] = ans[index] + i.se;
				q.push({ans[i.fi],i.fi});//在找到满足条件的值之后再入队
			}
		}
	}
	cout<<ans[b]<<endl;
}

signed main()// Don't forget pre_handle!
{
	IOS
	int T=1;
	cin>>T;
	while(T--) solve(); 
	return 0;
}

以上内容就是关于Dijkstra算法的两种实现思路了，感兴趣的小伙伴可以收藏起来到整理模版的时候直接食用！