P1064 [NOIP 2006 提高组] 金明的预算方案 题解

P1064 NOIP 2006 提高组 金明的预算方案 - 洛谷

参考P1064 NOIP 2006 提高组 金明的预算方案 - 洛谷

参考Anguei博主的解题思路，仅供自己做笔记自用

基本思路

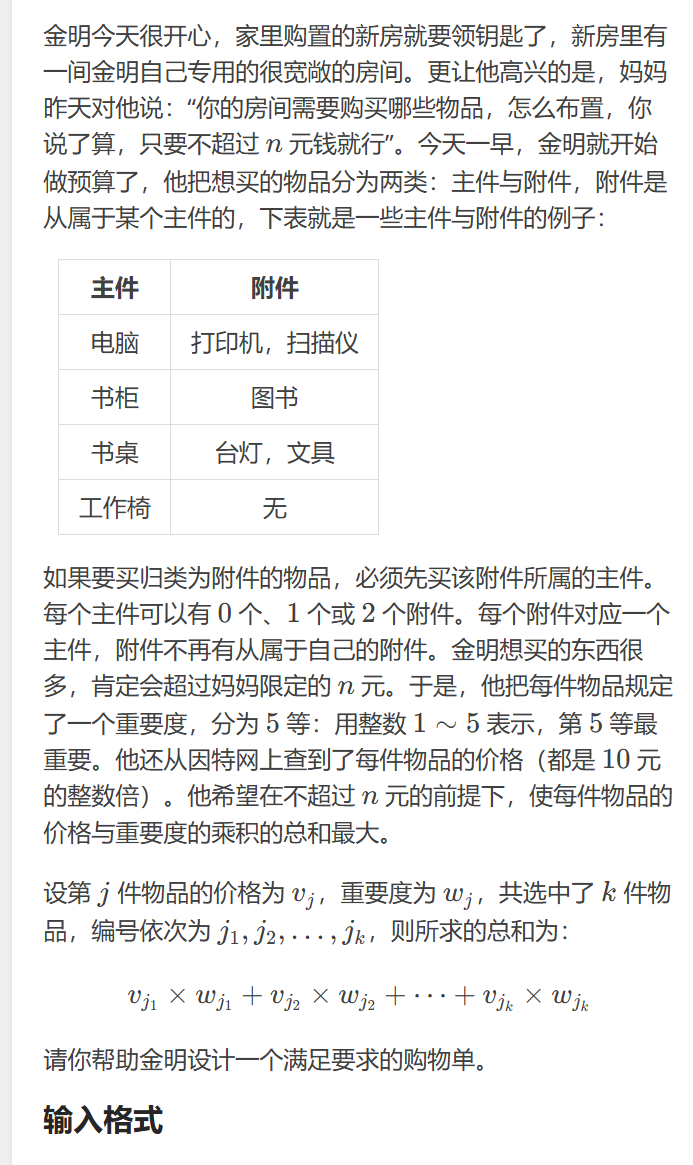
既然物品分为主件和附件两类，且每个主件最多包含两个附件，那么我们不妨枚举所有的主件，对于每次枚举，会有5种情况：
1.什么都不买
2.只买主件
3.买主件和第一个附件
4.买主件和第二个附件
5.买主件和两个附件
只要把这5种情况最终的价值算出来，取最大值就可以了。

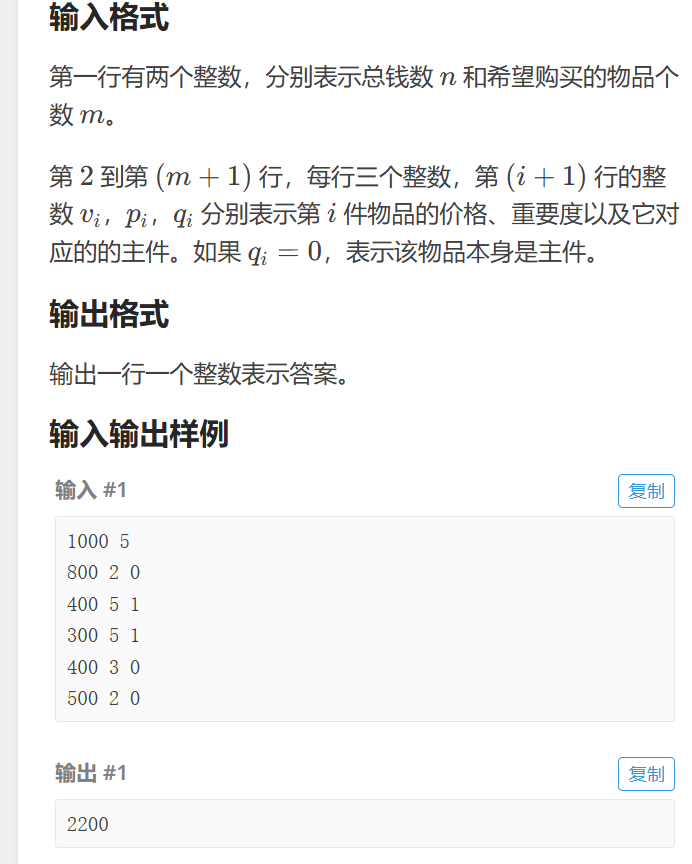
如何开数组？

建立两个二维数组 V65,3 和 P65,3，含义如题目描述。Vi,j 和 Pi,j 分别表示第 i 个物品的第 j 个附件的价格和重要度（当 j=0 时，表示主件）。

如何预处理数组？

1.如果是主件，则Vi,0,Pi,0=_v,_p。
2. 如果是物品 _q 的第 j 个附件，则令 Vq,j,Pq,j=_v,_p。

动态转移方程

代码简化

完整代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define ll long long
ll v[N][3],p[N][3],q[N];
ll f[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        if(!c)
        {
            v[i][0]=a;
            p[i][0]=b;
        }
        else
        {
            if(v[c][1]==0)
            {
                v[c][1]=a;
                p[c][1]=b;
            }
            else
            {
                v[c][2]=a;
                p[c][2]=b;
            }
        }
    }
    for(int i=1;i<=m;i++)
    {
        for(int j=n;j>=0;j--)
        {
            auto cost2 = [v, p, i](int x, int y) { return v[i][x] + v[i][y]; };
            auto cost3=[v,p,i](int x,int y,int z) {return v[i][x]+v[i][y]+v[i][z]; };
            auto pr=[v,p,i](int x) { return v[i][x]*p[i][x]; };

            if(j>=v[i][0])
                f[j]=max(f[j],f[j-v[i][0]]+pr(0));
            if(j>=cost2(0,1))
                f[j]=max(f[j],f[j-cost2(0,1)]+pr(0)+pr(1));
            if(j>=cost2(0,2))
                f[j]=max(f[j],f[j-cost2(0,2)]+pr(0)+pr(2));
            if(j>=cost3(0,1,2))
                f[j]=max(f[j],f[j-cost3(0,1,2)]+pr(0)+pr(1)+pr(2));
        }
    }
    cout<<f[n]<<endl;
    return 0;
}