快速排序
讲解
快速排序是基于分治来做的。
那么问题来了,分治又是什么呢?
分治,简单来说,就是"分而治之"的意思。基本思路是把一个大问题拆分成几个小问题,如果这些小问题还比较大,就继续拆,直到这些问题变得足够简单,可以直接解决。解决了所有的小问题之后,再把这些解决方案合并起来,就能解决原来的大问题了。
那分治又是怎么工作的?
基本来看大致是这么个流程:选择基准 -> 分割 -> 递归排序
- 选择分界点:从数列中挑出一个元素作为分界点。
- 分割:以分界点为界将序列一分为二。所有比基准小的元素放到基准前面,所有比基准大的元素放到基准后面(相同的数可以放到任一边)。
- 递归排序:对两个子序列(一个是基准左边的序列,另一个是基准右边的序列)重复上述步骤,直到每个序列里只剩下一个元素或者为空为止。
通过这种方式,一个复杂的问题(给一组数排序)被分解成了一些简单的子问题(每次只关注于排序一个小的子序列),这正是分治思想的核心。然后,通过解决这些子问题,并将它们的结果合并起来,我们就能够解决原始的问题。
那分治就这么随意吗?当然不是,在实际情况会复杂许多。
首先就是确定分界点:首先我们可以想象一个数列,最左边界索引 为l,最右边界索引 为r。那么分界点就会有以下四种情况:q[l],q[r],q[(l+r)/2],随机
注意分界点不是一个数值,而是数组的索引。
所以就可以根据以上步骤总结出模板了。
暴力的模板
- 新开两个数组a与b,用于存储一分为二之后的子序列
- 将要分治操作的序列看作是新开的数组q
- 在数组q上确定分界点,也就是索引,并确定索引上的值
- 然后递归处理数组q,小于等于的数值放进数组a,大于等于的数值放进数组b
- 最后将a,b两个数组拼起来,放进数组q
这么做需要开辟一个额外空间。就不用演示了,没有技术含量。
做题模板
- 定义指针i指向数组最左边界l,定义指针j指向数组最右边界r,并定义分界点
- i指针一直往分界点走,直到遇见比分界点处的数大的数,停止,那这时候就应该把i指针所指的数移到分界点的右侧
- 那么这个时候i指针不动,移动j指针,j指针一直往分界点走,停止,直到遇见比分界点处小的数,那这时候就应该把j指针所指的数移到分界点的左侧
- 那么两个指针都停下来了,而且所指的数都是错位的,那么swap进行交换就可以,让错位的数对号入座
- 一直递归直到i,j指针相遇,就完成了
模板题
解法
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int n;
int q[N];
void quick_sort(int q[], int l, int r) {
// 1. 判断是否是有效区间:没有数或者是只有一个数
if (l >= r) return;
// 两个指针需要先移动一次再去做判断(与下面的dowhile对应)
// 所以需要有预先的偏移量(l-1与j+1)
// 2. 确定指针与分界点
int i = l - 1, j = r + 1, x = q[l + r >> 1];
// 3. 使用dowhile指针正常移动,swap递归交换
while (i < j) {
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i],q[j]);
}
// 4. 传入左右两段,进行递归处理
quick_sort(q, l, j);
quick_sort(q, j+1, r);
// quick_sort(q, l, i - 1);
// quick_sort(q, i, r);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
quick_sort(q, 0, n - 1); // 注意这里传入的是索引,所以要n - 1
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}基本步骤
判断是否是有效区间:没有数或者是只有一个数
确定指针与分界点
使用dowhile进行指针的移动与比较,swap递归交换
传入左右两段,进行递归处理
注意事项
- 因为两个指针需要先移动一次再去做判断(与下面的dowhile对应,所以需要有预先的偏移量(l-1与j+1)
- do(i++); while (q[i] <= x);do(j--); while (q[j] >= x);这是错误的写法。
举个例子:传入的数组为[2, 2, 2, 2, 2],
i会一直增加,直到越界;j会一直减少,直到越界,那么i和j永远不会停下来,或者最终i超出数组范围。
练习题
归并排序
讲解
归并排序也是一种分治算法。它的基本思想是:
- 分:将原数组分成两个子数组;
- 治:递归地对子数组分别进行归并排序;
- 合:将两个有序子数组合并成一个有序数组。
模板题
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int n, q[N], tmp[N];
void merge_sort(int q[], int l ,int r) {
// 1.判断是否是有效区间:一个数或者没有数
if (l >= r) return;
// 2.确定分界点:mid = (l+r)/2
int mid = l + r >> 1;
// 3.从分界点开始,将原数组分成两个子数组
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
// 4.定义两个数组分别对应的初始双指针与临时数组tmp的计数k
int k = 0, i = l, j = mid + 1;
// 5.双指针 i 和 j 分别遍历左右两个子数组,按顺序把较小的元素放入tmp
while (i <= mid && j <= r) {
if (q[i] <= q[j]) {
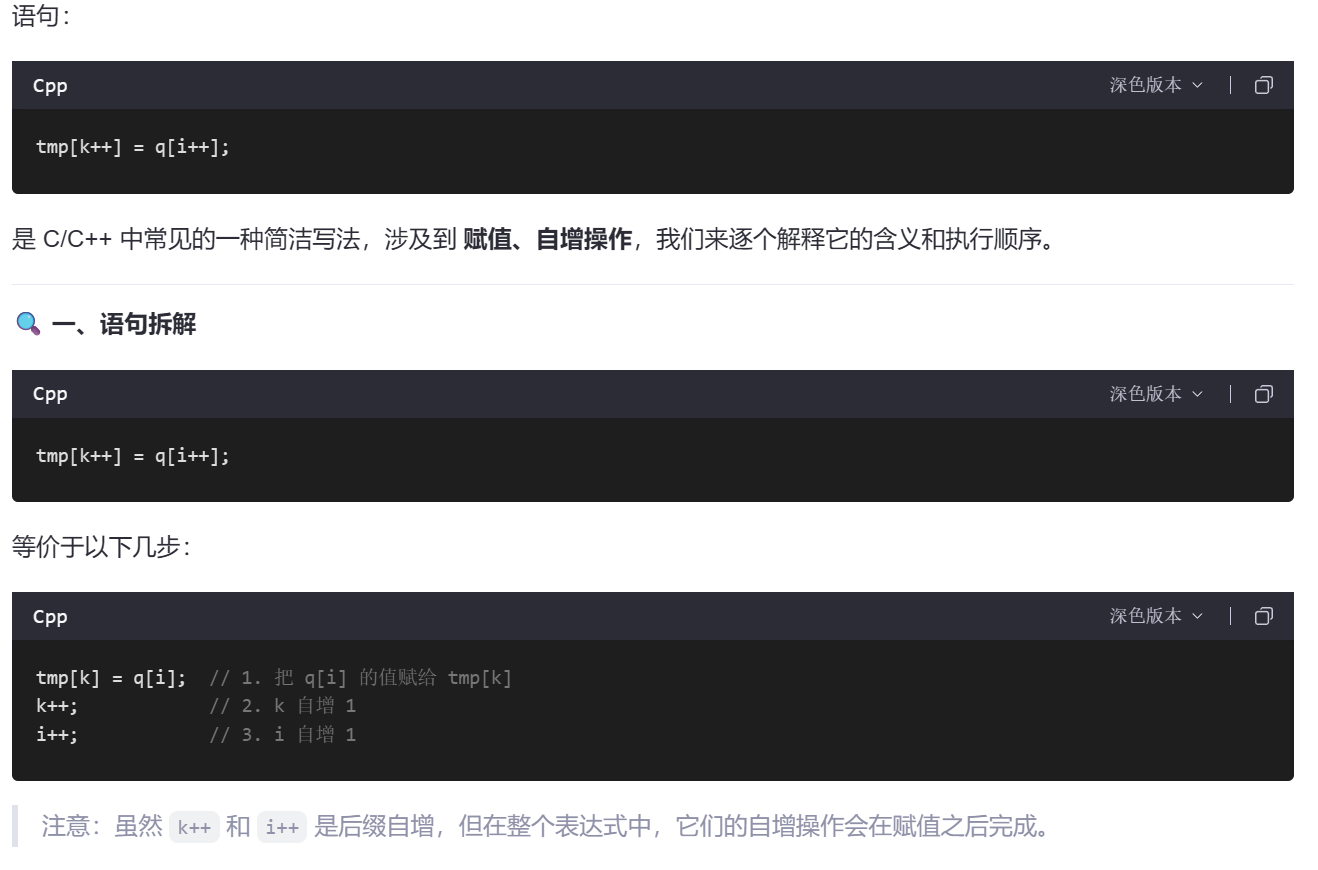
tmp[k++] = q[i++];
} else {
tmp[k++] = q[j++];
}
}
// 6.处理剩余元素(其中一个子数组可能还有未处理的元素)
while (i <= mid) {
tmp[k++] = q[i++];
}
while (j <= r) {
tmp[k++] = q[j++];
}
// 7.将临时数组复制回原数组
for (i = l, j = 0; i <= r; i++, j++) {
q[i] = tmp[j];
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &q[i]);
}
merge_sort(q, 0, n - 1);
for (int i = 0; i < n; i++) {
printf("%d ", q[i]);
}
return 0;
}基本步骤
1.判断是否是有效区间:一个数或者没有数
2.确定分界点:mid = (l+r)/2
3.从分界点开始,将原数组分成两个子数组
4.定义两个数组分别对应的初始双指针,以及临时数组的计数k
5.双指针遍历两个数组,按顺序把较小数放入临时数组
6.处理剩余元素
7.临时数组复制到原数组
注意事项
练习题
快速排序与归并排序的区别
| 序算法 | 思想 |
|---|---|
| 快速排序 | 选择一个基准元素,将数组划分为两个子数组:左边小于等于基准,右边大于等于基准,然后递归地对子数组排序。 |
| 归并排序 | 将数组分为两个子数组,分别排序后合并(先递归排序,后合并)。 |
| 排序算法 | 划分方式 |
|---|---|
| 快速排序 | 原地划分不需要额外空间,通过交换元素完成划分。 |
| 归并排序 | 非原地划分需要一个临时数组来合并两个有序子数组。 |
| 排序算法 | 稳定性 |
|---|---|
| 快速排序 | 不稳定(交换可能破坏相同元素的相对顺序) |
| 归并排序 | 稳定(合并时优先左边数组元素) |
| 快速排序 | 归并排序 |
|---|---|
| 使用双指针 i 和 j 从两端向中间扫描,找到不符合条件的元素进行交换 | 拆分到最小单位后,再合并两个有序数组 |
| 不需要额外空间(原地排序) | 需要一个临时数组 tmp[] 来合并数据 |
| 特性 | 快速排序 | 归并排序 |
|---|---|---|
| 时间复杂度 | 平均 O(n log n),最坏 O(n²) | 始终 O(n log n) |
| 空间复杂度 | O(log n) | O(n) |
| 稳定性 | 不稳定 | 稳定 |
| 是否原地排序 | 是 | 否 |
| 适用场景 | 内排序、速度快 | 外排序、稳定排序 |